Cím:	A Winkler-féle szögharmadolási módszerről
Szerző(k):	Dr. Elek Tibor
Füzet:	1937/május, 261 - 267. oldal	PDF  |  MathML
Témakör(ök):	Szakmai cikkek

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. A Winkler-féle szögharmadolási módszerről.${}^{*}$   I. Szögtávolságok összefüggése.   $1^{\circ }$. Szögtávolságnak fogjuk nevezni egy szög szárai közé húzott körív húrját. Minden szögtávolság merőleges a szög felezőjére. 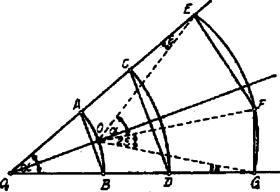    1. ábra   Rajzoljunk a tetszőleges $\alpha$ szög $O_1$ csúcsából a szárak közé $a$ sugárral $\widehat{AB}$ ívet (l. 1. ábra), majd a $b\ge \frac{\overline{AB}}{2}$ sugárral $\widehat{CD}$ ívet. Ezek után az $\widehat{AB}$ ív 0 felezőpontjából ugyancsak $b$ sugárral meghúzzuk az $\alpha$ szög szárai közé az $\widehat{EG}$ ívet. Erre az ívre az előbbi $\overline{AB}$ és $\overline{CD}$ szögtávolságok egymásután pontosan rámérhetők: $\overline{EF}=\overline{CD}$ és $\overline{FG}=\overline{AB}$. Ugyanis, ha $\overline{O_{1}A}=a$ és $\overline{O_{1}C}=\overline{OE}=b$, akkor $\begin{array}{c}{\displaystyle \overline{AB}=2a\text{sin}\frac{\alpha }{2}\text{és}\overline{CD}=2b\text{sin}\frac{\alpha }{2}\text{...}}\end{array}$ (1) Legyen $O_{1}EO\sphericalangle =O_{1}GO\sphericalangle =\epsilon$, akkor az $O_{1}EOG$ deltoid $O$-nál levő szöge: ${360}^{\circ }-\left(\alpha +2\epsilon \right)$ és így $EOG\sphericalangle =\alpha +2\epsilon$. Jelöljük $F$-fel az $\widehat{EG}$ ív azon pontját, melyre $\begin{array}{c}{\displaystyle EF=CD=2b\text{sin}\frac{\alpha }{2}\text{...}}\end{array}$ (1a) ekkor $EOF\Delta \underset{}{\overset{\infty }{=}}C{O}_{1}D\Delta$ és így $EOF\sphericalangle =\alpha$, miért is $FOG\sphericalangle =2\epsilon$ és így: $\begin{array}{c}{\displaystyle FG=2b\text{sin}\epsilon \text{...}}\end{array}$ (1b) Ámde az $OE{O}_1\Delta$-ből a sinustélellel: $\begin{array}{c}{\displaystyle a:b=\text{sin}\epsilon :\text{sin}\frac{\alpha }{2};\text{innen}\text{sin}\epsilon =\frac{a}{b}\text{sin}\frac{\alpha }{2}}\end{array}$ és 1b)-ből: $\begin{array}{c}{\displaystyle FG=2a\text{sin}\frac{\alpha }{2}=AB\mathrm{.}\text{...}}\end{array}$ (1c)  Q. e. d   $2^{\circ }$. Ha $b=a$ (l. 2. ábra), akkor a $\widehat{CD}$ ív egybeesik $\widehat{AB}$-vel és így az $\widehat{EG}$ ívre az $\overline{AB}$ szögtávolság most pontosan kétszer mérhető föl: $\overline{EF}=\overline{FG}=\overline{AB}$. Osszuk az $\widehat{EG}$ ívet a $H$, $F$, $I$ pontokkal négy egyenlő részre. Az $\overline{O_{1}H}=\overline{O_{1}I}$ sugárral húzott $\widehat{KL}$ ívre az $\overline{AB}$ szögtávolság szintén kétszer mérhető föl: 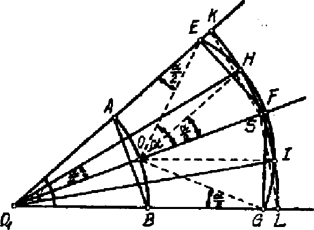$\overline{KS}=\overline{SL}=\overline{AB}$.     2. ábra   Ugyanis most $\begin{array}{c}{\displaystyle \overline{AB}=\overline{EF}=\overline{FG}=2a\text{sin}\frac{\alpha }{2}\mathrm{,}\text{...}}\end{array}$ (2) és a $HO{O}_1$ egyenlőszárú háromszögből, mivel $\overline{O_{1}O}=\overline{OH}=a$ és $H{O}_{1}O\sphericalangle =O_{1}HO\sphericalangle =\frac{\alpha }{4}$, azért $\begin{array}{c}{\displaystyle \overline{O_{1}H}=2a\text{cos}\frac{\alpha }{4}=\overline{O_{1}I}=\overline{O_{1}K}=\overline{O_{1}L}\text{...}}\end{array}$ (2a) Most már $\begin{array}{c}{\displaystyle \overline{KS}=\overline{SL}=2\overline{O_{1}K}\cdot \text{sin}\frac{\alpha }{4}=4a\text{sin}\frac{\alpha }{4}\text{cos}\frac{\alpha }{4}=2a\text{sin}\frac{\alpha }{2}=\overline{AB}\mathrm{.}}\end{array}$ (2b)  Q. e. d 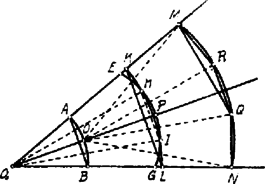    3. ábra   $3^{\circ }$. Az $\widehat{AB}$ ív $O$ felezőpontjából (l. 3. ábra) most az előbbi $\overline{O_{1}K}=\overline{O_{1}L}$ sugárral húzzunk az $\alpha$ szög szárai közé $\widehat{MN}$ ívet. Erre az $1^{\circ }$. pont szerint a $\overline{KL}$ és $\overline{AB}$ szögtávolságok egymásután pontosan felmérhetők. $\overline{MQ}=\overline{KL}$ és $\overline{QN}=\overline{AB}$. Viszont az $\widehat{MQ}=\widehat{KL}$ ívre az $\overline{AB}$ szögtávolság kétszer mérhető rá: $\overline{MR}=\overline{RQ}=\overline{AB}$ és így az $\widehat{MN}$ ívre végül is háromszor mérhető föl $\overline{AB}$. Az $MON\sphericalangle$-et az $OR$, $OQ$ sugarak ilyenformán 3 egyenlő részre osztják, de az eredeti $M{O}_{1}N\sphericalangle =\alpha$ szöget az $O_{1}R$, $O_{1}Q$ sugarak nem.   II. Az egyenes szög (${180}^{\circ }$) harmadolása.   $4^{\circ }$. Legyen adva egy $k$ kör $O$ középponttal (l. 4. ábra). Szerkesszük meg a vele koncentrikus $k_1$ kört úgy, hogy a $k_1$ körbe írható szabályos húrháromszög oldala az eredetileg megadott $k$ kör sugarával legyen egyenlő: 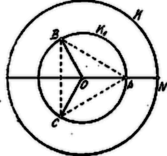${\displaystyle \begin{array}{c}\hfill {\displaystyle \overline{AB}=\overline{ON}=r\mathrm{.}}\hfill \\ \hfill {\displaystyle \overline{AB}=\overline{OA}\sqrt[]{3}\mathrm{,}\text{azért}r=r_1\sqrt[]{3}\mathrm{,}\text{ill.}{r}_1=\frac{r}{\sqrt[]{3}}\text{...}}\hfill & \text{(<mn>3</mn>)}\end{array}}$     4. ábra   A $k_1$ kör pontosan is megszerkeszthető, mi azonban egy közelítő szerkesztést fogunk alkalmazni, mely azután bármely szög harmadolásánál is felhasználhatónak fog bizonyulni. Vegyük körzőbe a $k$ körbe írt szabályos nyolcszög $\overline{NL}$ oldalát (l. 5. ábra) és az $\overline{ON}$ sugár $F$ felezőpontjából e körzőnyílással messük el a rá merőleges sugarat. Az így kapott $P$ pont a keresett $k_1$ kör kerületén van. E módszer azonban nem pontos, hanem a $k_1$-nél kissé nagyobb sugarú kört ad. 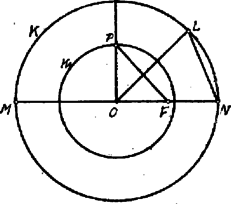    5. ábra   T. i.: $\begin{array}{c}{\displaystyle \overline{NL}=a_8=2r\text{sin}{22}^{\circ }30\text{'}=2r\sqrt[]{\frac{1-\text{cos}{45}^{\circ }}{2}}=2r\sqrt[]{\frac{1-\frac{\sqrt[]{2}}{2}}{2}}=r\sqrt[]{2-\sqrt[]{2}}=\overline{PF}\text{...}}\end{array}$ (4) és így $\begin{array}{c}{\displaystyle \overline{OP}=\sqrt[]{{\overline{PF}}^2-\frac{r^2}{4}}=\sqrt[]{r^2\left(2-\sqrt[]{2}\right)-\frac{r^2}{4}}=r\sqrt[]{\frac{7}{4}-\sqrt[]{2}}\text{...}}\end{array}$ (4a) Az $\overline{OP}\approx r_1$ állítás tehát egyértelmű azzal az állítással, hogy $\begin{array}{c}{\displaystyle \frac{7}{4}-\sqrt[]{2}\approx \frac{1}{3}\mathrm{,}\text{azaz}\sqrt[]{2}\approx \frac{7}{4}-\frac{1}{3}=\frac{17}{12}=1\mathrm{,}416\text{...}}\end{array}$ (4b) ami a $\sqrt[]{2}=1\mathrm{,}4142\text{...}$ értékhez képest 0,0024-nyi hibát jelent ($0\mathrm{,}17\%$-os hiba). Végül is $\begin{array}{c}{\displaystyle \overline{OP}=r_1\cdot 1\mathrm{,}00346\text{...}}\end{array}$ (4c) vagyis szerkesztésünk valóban a $k_1$-nél kissé nagyobb sugarú kört ad. 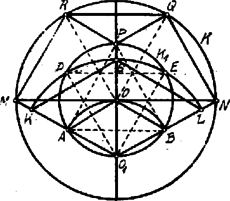    6. ábra   $5^{\circ }$. Húzzuk meg most már (l. 6. ábra) a $k$ kör $\overline{MN}$ átmérőjét, valamint a $k_1$ körnek erre merőleges $\overline{O_{1}P}$ átmérőjét és a $k_1$ körbe írt szabályos $ABP$, $O_{1}DE$ háromszögek többi oldalait. Mivel $\overline{MO}=\overline{AB}=\overline{ON}$ és $MO\parallel AB\parallel ON$, azért az $ABOM$, $ABNO$ négyszögek parallelogrammák. Továbbá, mint a $k_1$ körbe írt szabályos hatszög oldalai: $\overline{A{O}_1}=\overline{O_{1}B}=\overline{BO}=\overline{OA}$ és így az $A{O}_{1}BO$ négyszög rombusz, melyben $A{O}_{1}B\sphericalangle =AOB\sphericalangle ={120}^{\circ }$. A ${180}^{\circ }$-os $MON\sphericalangle$ és a ${120}^{\circ }$-os $M{O}_{1}N\sphericalangle$ ugyanolyan viszonyban vannak, mint a 3. ábrabeli $MON\sphericalangle$ és $M{O}_{1}N\sphericalangle$. Utóbbi szög szárai közé itt is húzzuk meg $O_1$ középpontból az $O$ ponton átmenő $\widehat{AB}$ ívet és a $D$, $E$ pontokon átmenő $\widehat{KL}$ ívet. Ha a $K$ kör sugara: $r$, akkor az I. rész fejtegetései szerint az egyes ívekre a köv. szögtávolságok mérhetők föl: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle \text{az }\widehat{AB}\text{ ívre: }}& {\displaystyle \overline{AB}=r\mathrm{,}}\hfill \\ \hfill {\displaystyle \text{a }{k}_1\text{ kör }\widehat{APB}\text{ ívére: }}& {\displaystyle \overline{AP}+\overline{PB}=2r\mathrm{,}}\hfill \\ \hfill {\displaystyle \text{a }\widehat{KL}\text{ ívre: }}& {\displaystyle \overline{KG}+\overline{GL}=2r\mathrm{,}}\hfill \\ \hfill {\displaystyle \text{és a }k\text{ kör }\widehat{MN}\text{ ívére: }}& {\displaystyle \overline{MR}+\overline{RQ}+\overline{QN}=3r\mathrm{.}}\hfill \end{array}}$ Az $MN$ ívet harmadoló $R$, $Q$ pontok $O$-val együtt szabályos háromszöget alkotnak, mely az $O_{1}DE\Delta$-ből keletkezik, ha ezt az $\overrightarrow{O_{1}O}$ translationak vetjük alá. Ennélfogva az $ORQ\Delta$ középpontja a $P$ pont és így $\overline{OP}=\overline{PR}=\overline{PQ}$. (Megjegyzendő, hogy ez a 3. ábrabeli $ORQ\Delta$-re is vonatkozik, mely az $O_{1}HI\Delta$ translatiójából keletkezik és így ott is $\overline{OP}=\overline{PR}=\overline{PQ}$). Ezek figyelembevételével a ${180}^{\circ }$-os $MON\sphericalangle$ harmadolására, vagyis az $R$, $Q$ pontok megszerkesztésére két eljárást is nyertünk: az $MON\sphericalangle$ szárai közé meghúzzuk a $k$ kör $\widehat{MN}$ ívét, majd az $MON\sphericalangle$ felezőjén a $4^{\circ }$. pontban ismertetett módszerrel megkeressük a $k_1$ kört megadó $P$ pontot. Ezek után az egyik eljárás abban áll, hogy az $O$ ponton túl meghosszabbított szögfelezőre rámérjük az $\overline{O_{1}O}=\overline{OP}$ távolságot és az $M{O}_{1}N\sphericalangle$ szárai közé $\overline{O_{1}O}$ sugárral az $\widehat{AB}$ ívet rajzoljuk. Ekkor az $\overline{AB}$ szögtávolság éppen háromszor mérhető rá az $\widehat{MN}$ ívre: $\overline{MR}=\overline{RQ}=\overline{QN}=\overline{AB}$. A másik eljárás a következő: $P$ pontba beszúrva a körzőt, $\overline{OP}$ sugárral elmetsszük az $\widehat{MN}$ ívet: így éppen az $R$, $Q$ pontokat kapjuk.   III. A szögharmadolás három módszere.   $6^{\circ }$. A ${180}^{\circ }$-os szög harmadolásának iménti végrehajtása kiterjeszthető minden más szögre is. Így a szögharmadolás három módszerét kapjuk. 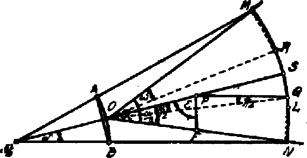    7. ábra   Az első módszer szerint (l. 7. ábra) az $\alpha$ szög szárai közé húzott $\widehat{MN}$ ívet négy egyenlő részre osztjuk, azután az $\overline{NL}$, negyedívtávolságot körzőbe vesszük és az $\overline{ON}$ sugár $F$ felezőpontjából e körzőnyílással elmetsszük a szögfelezőt $P$ pontban (a két metszéspont közül az $\widehat{MN}$ ívhez közelebb fekvőt vesszük). Meghosszabbítva $O$ ponton túl a szögfelezőt és rámérve az $\overline{O_{1}O}=\overline{OP}$ távolságot, az $M{O}_{1}N\sphericalangle$ szárai közé most is meghúzzuk $\overline{O_{1}O}$ sugárral az $\widehat{AB}$ ívet. Az $\overline{AB}$ szögtávolság az $\widehat{MN}$ ívre háromszor mérhető föl: $\overline{MR}=\overline{RQ}=\overline{QN}=\overline{AB}$. Az $MOR\sphericalangle =\omega$ szög tehát közelítőleg $\frac{\alpha }{3}$-mal egyenlő. (Ez a szerkesztés mintegy megfordítottja a 3. ábrán látható szerkesztésnek és annak pontossága itt csak azért tűnik el, mert az $\overline{O_{1}O}$ távolság itt adott megszerkesztése nem pontos, mint ahogy ez a távolság körzővel és vonalzóval pontosan nem is szerkeszthető meg.) Egyszerűség kedvéért legyen $\overline{OM}=\overline{ON}=1$, tehát $\overline{OF}=\frac{1}{2}$. A negyedívtávolság: $\begin{array}{c}{\displaystyle \overline{NL}=2\text{sin}\frac{\alpha }{8}=FP\text{...}}\end{array}$ (5) Legyen $OPF\sphericalangle =\epsilon$, ekkor az $OFP\Delta$-ben a sinustétellel: $\begin{array}{c}{\displaystyle \text{sin}\epsilon :\text{sin}\frac{\alpha }{2}=\frac{1}{2}:2\text{sin}\frac{\alpha }{8};\text{innen}\text{sin}\epsilon =\frac{\text{sin}\frac{\alpha }{2}}{4\text{sin}\frac{\alpha }{8}}\text{...}}\end{array}$ (5a) Mivel pedig $\begin{array}{c}{\displaystyle \text{sin}\frac{\alpha }{2}=2\text{sin}\frac{\alpha }{4}\text{cos}\frac{\alpha }{4}=4\text{sin}\frac{\alpha }{8}\text{cos}\frac{\alpha }{8}\text{cos}\frac{\alpha }{4}\text{...}}\end{array}$ (5b) azért 5a)-ból: $\begin{array}{c}{\displaystyle \text{sin}\epsilon =\text{cos}\frac{\alpha }{4}\text{cos}\frac{\alpha }{8}\text{...}}\end{array}$ (5c) Ezekután $\begin{array}{c}{\displaystyle \overline{OP}:\overline{FP}=\text{sin}\left(\frac{\alpha }{2}+\epsilon \right):\text{sin}\frac{\alpha }{2}\text{...}}\end{array}$ (5d) (A $P$ pont másik lehetséges helyzetében $\epsilon$ helyett ${180}^{\circ }-\epsilon$ volna írandó). Most már az 5d)-ből, figyelembevéve $FP$-nek 5) alatti értékét és az 5a) összefüggést: $\begin{array}{c}{\displaystyle \overline{OP}=\frac{2\text{sin}\frac{\alpha }{8}\text{sin}\left(\frac{\alpha }{2}+\epsilon \right)}{\text{sin}\frac{\alpha }{2}}=\frac{\text{sin}\left(\frac{\alpha }{2}+\epsilon \right)}{2\text{sin}\epsilon }=\frac{\text{sin}\frac{\alpha }{2}\text{cos}\epsilon +\text{cos}\frac{\alpha }{2}\text{sin}\epsilon }{2\text{sin}\epsilon }\mathrm{,}}\end{array}$ ill. 5b) és 5c) alapján: $\begin{array}{c}{\displaystyle \overline{OP}=\frac{4\text{sin}\frac{\alpha }{8}\text{cos}\frac{\alpha }{8}\text{cos}\frac{\alpha }{4}\text{cos}\epsilon +\text{cos}\frac{\alpha }{2}\text{cos}\frac{\alpha }{4}\text{cos}\frac{\alpha }{8}}{2\text{cos}\frac{\alpha }{4}\text{cos}\frac{\alpha }{8}}=2\text{sin}\frac{\alpha }{8}\text{cos}\epsilon +\frac{1}{2}\text{cos}\frac{\alpha }{2}\text{...}}\end{array}$ (5e) Tisztán az $\alpha$-val kifejezve pedig: $\begin{array}{c}{\displaystyle \overline{OP}=2\text{sin}\frac{\alpha }{8}\sqrt[]{1-\text{cos}{}^2\frac{\alpha }{4}\text{cos}{}^2\frac{\alpha }{8}}+\frac{1}{2}\text{cos}\frac{\alpha }{2}=\overline{O_{1}O}=\overline{O_{1}A}=\overline{O_{1}B}\text{...}}\end{array}$ (6) Az $O{O}_{1}N\Delta$-ből a cosinustétellel: Most már az $M{O}_{1}O\sphericalangle =O{O}_{1}N\sphericalangle =\delta$ szög kiszámítható a sinustétellel: $\begin{array}{c}{\displaystyle \text{sin}\delta :\text{sin}\left({180}^{\circ }-\frac{\alpha }{2}\right)=1:O_{1}N\mathrm{,}\text{tehát}\text{sin}\delta =\frac{\text{sin}\frac{\alpha }{2}}{\overline{O_{1}N}}\text{...}}\end{array}$ (6b) Az $\overline{AB}$ szögtávolság: $\begin{array}{c}{\displaystyle \overline{AB}=2\overline{O_{1}A}\cdot \text{sin}\delta =2\frac{\overline{O_{1}O}}{\overline{O_{1}N}}\text{sin}\frac{\alpha }{2}=\overline{MR}\text{...}}\end{array}$ (6c) A keresett $MOR\sphericalangle =\omega$ szögre tehát felírhatjuk, hogy $\begin{array}{c}{\displaystyle \text{sin}\frac{\omega }{2}=\frac{\overline{MR}}{2\overline{OM}}=\frac{\overline{MR}}{2}=\frac{\overline{O_{1}O}\cdot \text{sin}\frac{\alpha }{2}}{\overline{O_{1}N}}\text{...}\mathrm{,}}\end{array}$ (6d) ill. 6) és 6a) alapján: $\begin{array}{c}{\displaystyle \text{sin}\frac{\omega }{2}=\frac{2\text{sin}\frac{\alpha }{2}\text{sin}\frac{\alpha }{8}\sqrt[]{1-\text{cos}{}^2\frac{\alpha }{4}\text{cos}{}^2\frac{\alpha }{8}}+\frac{1}{4}\text{sin}\alpha }{\sqrt[]{1+\frac{1}{4}\text{cos}\alpha +\text{cos}{}^2\frac{\alpha }{2}+4\text{sin}{}^2\frac{\alpha }{8}+6\text{cos}\frac{\alpha }{2}\text{sin}\frac{\alpha }{8}\sqrt[]{1-\text{cos}{}^2\frac{\alpha }{4}\text{cos}{}^2\frac{\alpha }{8}}}}\mathrm{.}}\end{array}$ (7) E képlet az $\omega \approx \frac{\alpha }{3}$ szöget, mint $\alpha$ függvényét szolgáltatja. Értéktáblázatából (l. alább) kiderül, hogy e szerkesztéssel csak az első 3 negyed-beli szögek közelítő harmadolása végezhető el, a 4-ik negyedben már igen nagy az eltérés. Minthogy $\alpha ={210}^{\circ }$-nál $\omega >\frac{\alpha }{3}$, de már $\alpha ={240}^{\circ }$-nál $\omega <\frac{\alpha }{3}$, azért kell lennie egy olyan ${210}^{\circ }<x<{240}^{\circ }$ értéknek, melyre $\omega =\frac{x}{3}$. Az $x$ szög közelítő értéke lineáris interpolációval meg is állapítható. Az $\omega =f\left(\alpha \right)$ függvény görbéjének e szakaszát ugyanis egyenesnek véve, felírható a köv. aránylat: $\begin{array}{c}{\displaystyle \left(x-{210}^{\circ }\right):\left({240}^{\circ }-x\right)=\left({70}^{\circ }8\text{'}14\text{'}\text{'}-{70}^{\circ }\right):\left({80}^{\circ }-{79}^{\circ }49\text{'}52\text{'}\text{'}\right)\mathrm{,}\text{ melyből }x={223}^{\circ }26\text{'}54\text{'}\text{'}}\end{array}$ (7a) Ez tehát közelítőleg az $\alpha$ szög, melynek harmadrészét szerkesztésünk pontosan adja meg. Ha már most egy 4-ik negyedben levő $\alpha$ szöget akarunk harmadolni, akkor vagy a ${360}^{\circ }-\alpha$ hegyes szöget harmadoljuk és harmadrészét kivonjuk $\frac{{360}^{\circ }}{3}=120$-ból, vagy pedig $\frac{\alpha }{2}$-t harmadoljuk és a kapott szöget kétszer vesszük.   $7^{\circ }$. A ${180}^{\circ }$-os szög harmadolásánál talált másik eljárás is eredményre vezet: az előbb leírt módon megkeressük a szögfelezőn a $P$ pontot, majd ide beszúrva a körzőt, $\overline{OP}$ sugárral elmetsszük az $\widehat{MN}$ ívet (l. 7. ábra). Az így kapott $R$, $Q$ pontok az $\widehat{MN}$ ívet közelítőleg ismét három egyenlő részre osztják. Most tehát az $OPQ\Delta$ egyenlőszárú; oldalainak hosszúsága 6) szerint: $\begin{array}{c}{\displaystyle \overline{OQ}=\mathrm{1,}\overline{OP}=\overline{PQ}=2\text{sin}\frac{\alpha }{8}\sqrt[]{1-\text{cos}{}^2\frac{\alpha }{4}\text{cos}{}^2\frac{\alpha }{8}}+\frac{1}{2}\text{cos}\frac{\alpha }{2}\text{...}}\end{array}$ (8) A $POQ\sphericalangle =\frac{\phi }{2}$ szögre felírhatjuk tehát: $\begin{array}{c}{\displaystyle \text{cos}\frac{\phi }{2}=\frac{\overline{OQ}}{2\overline{OP}}=\frac{1}{2\overline{OP}}\text{...}\mathrm{,}}\end{array}$ (8a) ill. $\begin{array}{c}{\displaystyle \text{cos}\frac{\phi }{2}=\frac{1}{4\text{sin}\frac{\alpha }{8}\sqrt[]{1-\text{cos}{}^2\frac{\alpha }{4}\text{cos}{}^2\frac{\alpha }{8}+\text{cos}\frac{\alpha }{2}}}\text{...}}\end{array}$ (9) E képlet az $ROQ\sphericalangle =\phi \approx \frac{\alpha }{3}$ szöget adja meg $\alpha$ függvényeként. Értéktáblázatából (l. alább) kiderül, hogy ez a szerkesztés is csak az első 3 negyed-beli szögekre alkalmazható közvetlenül. Közelítése e negyedekben rosszabb, mint az első szerkesztésé, a 4-ik negyedben azonban nem ad olyan nagy eltéréseket, mint az. Ismét ${210}^{\circ }$, és ${240}^{\circ }$ között találjuk meg ezt a szöget, melynek szerkesztésünk pontosan szolgáltatja a harmadrészét. A számítás eredménye most ${226}^{\circ }45\text{'}7\text{'}\text{'}$.   $8^{\circ }$. Legyen az $\widehat{MN}$ ív felezőpontja: $S$ (l. 7. ábra). Ha $\widehat{QN}=\frac{\widehat{MN}}{3}$, akkor: $\begin{array}{c}{\displaystyle \widehat{SO}=\frac{\widehat{MN}}{2}-\frac{\widehat{MN}}{3}=\frac{\widehat{MN}}{6}=\frac{\widehat{SN}}{3}\mathrm{,}\text{...}}\end{array}$ (10) vagyis a $Q$ pont megszerkesztésével az $\widehat{SN}$ ívet és az $SO\sphericalangle$-et is harmadoltuk. E felfogásban tehát a szögharmadolás a következőképpen végzendő (l. 8. ábra): Az $\alpha$ szög szárai közé húzott $\widehat{MN}$ ívet felezzük, azután az $\overline{NL}$ félívtávolságot körzőbe vesszük és az $\overline{ON}$ sugár $F$ felezőpontjából e körzőnyílással elmetsszük a szög másik szárát a $P$ pontban. (Ismét az $\widehat{MN}$ ívhez közelebb eső metszéspontot választjuk). Most e $P$ pontba szúrjuk a körzőt és az $\overline{OP}$ sugárral elmetsszük az $\widehat{MN}$ ívet: így az ívünket harmadoló $R$ pontot kapjuk. 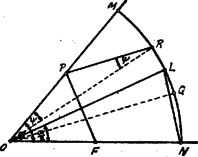    8. ábra   Az $OPR$ egyenlőszárú háromszög oldalai most: $\begin{array}{c}{\displaystyle \overline{OR}=\mathrm{1,}\overline{OP}=\overline{PR}=2\text{sin}\frac{\alpha }{4}\sqrt[]{1-\text{cos}{}^2\frac{\alpha }{2}\text{cos}{}^2\frac{\alpha }{4}}+\frac{1}{2}\text{cos}\alpha \mathrm{,}\text{...}}\end{array}$ (11) t. i. e szerkesztés úgy fogható fel, mintha az előbbi szerkesztést hajtottuk volna végre, de $2\alpha$ nagyságú szögön, tehát 8)-ban $\alpha$ helyett $2\alpha$ írandó. A $POR\sphericalangle =\psi$ szögre felírhatjuk tehát: $\begin{array}{c}{\displaystyle \text{cos}\psi =\frac{\overline{OR}}{2\overline{OP}}=\frac{1}{2\overline{OP}}\text{...}\mathrm{,}}\end{array}$ (11a) ill. $\begin{array}{c}{\displaystyle \text{cos}\psi =\frac{1}{4\text{sin}\frac{\alpha }{4}\sqrt[]{1-\text{cos}{}^2\frac{\alpha }{2}\text{cos}{}^2\frac{\alpha }{4}}+\text{cos}\alpha }\text{...}}\end{array}$ (12) A $\psi \approx \frac{\alpha }{3}$ szögnek, mint $\alpha$ függvényének értéktáblázatából kiderül, hogy e harmadik módszer kb. ${135}^{\circ }$-ig használható, ezentúl egyre rosszabb közelítést ad. Most ${113}^{\circ }22\text{'}33\text{'}\text{'}$, az előbbi szög fele az a szög, melynek harmadrészét e szerkesztés pontosan adja. Értéktáblázataink a következők:         * A 4-ik negyedben $\omega$ rohamosan esik. Közbülső értékek: ${345}^{\circ }$-nál $\omega ={79}^{\circ }9\text{'}40\text{'}\text{'}$; ${357}^{\circ }$-nál $\omega =8^{\circ }18\text{'}22\text{'}\text{'}$. ** A $\psi$ szög kb. $\alpha ={135}^{\circ }$-ig használható; itt $\psi ={44}^{\circ }24\text{'}13\text{'}\text{'}$.   Mint látható, tehát mindhárom szerkesztés csak közelítő és mindháromnak más a közelítési mértéke. Ujpest, 1937. február hó 6-án.  Dr. Elek Tibor ${}^{*}$Dr. Winkler Béla (1900‐1935.) korán elhunyt kiváló büntetőjogász, jogbölcsész és filozófus szakíró, aki matematikával és természettudományokkal is behatóan foglalkozott.