Cím: Egy Jensen tétel egyszerű bizonyítása
Szerző(k):  Klein Eszter 
Füzet: 1935/november, 65 - 67. oldal  PDF  |  MathML 
Témakör(ök): Szakmai cikkek

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Jelentsen f(x) egy homorú függvényt (Homorúnak az olyan görbét nevezem, amely alulról nézve homorú, tehát bármely két pontját összekötő görbeív e két pontot összekötő egyenes húr fölött van). Vegyünk fel n különböző abscissa értéket: x1, x2, ... xn. Az ezekhez tartozó függvényértékek: f(x1), f(x2) ... f(xn), akkor Jensen tétele azt mondja, hogy:

f(x1)+f(x2)+...+f(xn)n<f(x1+x2+...xnn).

Azaz szavakban: homorú függvénynél az ordináták számtani közepe nem lehet nagyobb, mint az abscissák számtani közepéhez tartozó függvényérték.
 

Domború függvénynek nevezem az olyat, amelynél két pontot összekötő görbeív e két pontot összekötő egyenes húr alatt van, akkor domború függvényre nézve:
f(x1)+f(x2)+...+f(xn)n≧f(x2+x2+...xnn).

Az egyenlőségjel mind a két esetben csak akkor léphet fel, ha a függvény képe egy egyenes.
Ezt a tételt a Cauchy‐féle egyenlőtlenség (a számtani és mértani közepekről) mintájára, teljes indukcióval szokták bizonyítani. Ehelyett egy egyszerű, geometriai szemléleten alapuló bizonyítást adunk és aztán ennek a tételnek a segítségével fogjuk bebizonyítani a Cauchy‐tételt is.
Ismeretes dolog, hogy ha a síkban adva van n pont: (x1,y1),(x2,y2)...(xn,yn), e pontok súlypontjának a koordinátái:
x1+x2+...xnn,y1+y2+...+ynn.

Ha az n adott pont egy konvex sokszöget képez, könnyen belátható, hogy a súlypont e sokszög belsejébe fog esni. Ha n=3, akkor ezt tudjuk. (Háromszög súlypontja mindig a háromszög belsejébe esik.) Alkalmazzunk teljes indukciót: tegyük fel, hogy az n-szögről már tudjuk, hogy súlypontja a sokszög belsejébe esik, és most fölveszünk egy n+1-edik pontot. Az egész rendszer súlypontja megváltozik és az új súlypontot megkapom, ha megalkotom ennek az n+1-edik pontnak és az előbbi súlypontnak a súlypontját, ez rajta lesz a kettő összekötő egyenesén, tehát nyilván a konvex sokszög belsejében.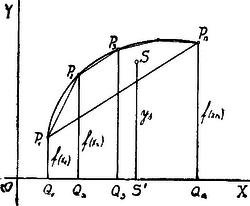
 
 

Képzeljünk el most már egy homorú függvényt. Egyszerűség kedvéért fölvehetjük, hogy f(x1), f(x2), ... f(xn), mindannyian pozitívok. Ha nem így lenne, akkor a függvényhez hozzáadunk egy elegendő nagy c számot, úgy, hogy f(x1)+c, f(x2)+c, ... f(xn)+c valamennyien pozitívok legyenek. Ezáltal a bizonyítandó egyenlőtlenség mindkét oldala c-vel nagyobbodik, ha tehát f(x)+c-re be tudom bizonyítani, akkor igaz az egyenlőtlenség f(x)-re is.
Vegyük szemügyre azt az n pontot, amelynek koordinátái rendre:
P1=[x1,f(x2],P2=[x2,f(x2)]...Pn=[(xn,f(xn)].
Ezek a pontok egy konvex sokszöget alkotnak, amely a homorú függvény alatt van, a definíció értelmében. A (P1,P3,...Pn) pontok súlypontja, S, e sokszög belsejében lesz. S pont koordinátái:
xs=x1+x2+⋯+xnnésys=f(x1)+f(x2)+⋯+f(xn)n.
Hogy az S pont a sokszög belsejében, illetve a homorú függvény alatt van, az precízen megfogalmazva azt jelenti, hogy az S pont ordinátája kisebb, mint az xs-hez tartozó függvényérték, vagyis:
f(x1)+f(x2)+⋯+f(xn)n<f(x1+x2+⋯+xnn).
Q. e. d.

Ha a függvény domború, akkor az S pont a függvény fölé esik, ordinátája tehát nagyobb lesz, mint az xs-hez tartozó függvényérték, domború függvénynél tehát:
f(x1)+f(x2)+⋯+f(xn)n>f(x1+x2+⋯xnn).
Ha a függvény képe egyenes, akkora súlypont ráesik az egyenesre, tehát
f(x1)+f(x2)+⋯+f(xn)n=f(x1+x2+⋯+xnn).

Alkalmazzuk ezt az egyenlőtlenséget arra az esetre, ha f(x)=logx. A log‐görbe homorú, tehát:
logx1+logx2+⋯+logxnn<logx1+x2+⋯+xnn.
Más szóval:
logx1x2...xnn<logx1+x-2+...xnn.
Ebből következik:
x1x2...xnn<x1+x2x+...xnn.
Azaz: n különböző pozitív szám mértani közepe mindig kisebb a számtani közepüknél; ez Cauchy‐tétele.
A bizonyítás változatlanul érvényben marad akkor is, ha megengedjük, hogy az x1, x2 ... xn között egyenlő x-ek is előforduljanak, akkor e súlypontot úgy kell értelmeznünk, mintha a P1, P2, ... Pn pontokba nem csupa egyenlő súlyt tennénk, hanem ha pl. x1 5-ször fordul elő, akkor P1-be 5-szörös súlyt képzelünk.
Budapest 1935 október.
Klein Eszter
okleveles középiskolai tanár.