Kezdőlap


Cím:	1930. évi OKTV-n Hapka István első díjat nyert dolgozata a mennyiségtanból
Szerző(k):	Hapka István
Füzet:	1930/szeptember, 2 - 4. oldal	PDF \| MathML
Témakör(ök):	OKTV

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

1^{\circ}

\begin{matrix} cos 2 x = 2 cos^{2} x - 1 és cos 2 y = 2 cos^{2} y - 1 \end{matrix}

összefüggések felhasználásával a (2) egyenlet

\begin{matrix} cos^{2} x + cos^{2} y = \frac{b + 2}{2} \end{matrix}

(*)

alakra hozható. Az (1)-ből

cos y = a - cos x

helyettesítéssel, a (2a) kellő rendezés után így alakul:

\begin{matrix} 4 cos^{2} x - 4 a cos x + 2 a^{2} - b - 2 = 0. \end{matrix}

(3)

Minthogy

cos x

és

cos y

felcserélhető, ugyanilyen alakú egyenletet kapunk

cos y

-ra is; tehát

cos x

és

cos y

\begin{matrix} 4 z^{2} - 4 a z + 2 a^{2} - b - 2 = 0 \end{matrix}

(4)

egyenlet gyökei; ha

z_{1} = cos x

, akkor

z_{2} = cos y

és megfordítva.

2^{\circ}

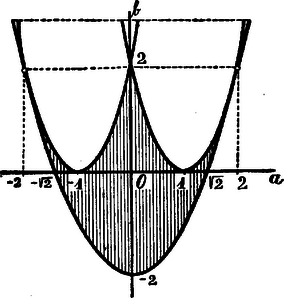
. A (4) egyenlet gyökei akkor felelnek meg, ha valósak, továbbá, ha

- 1

és

+ 1

között vannak.
Valósak a gyökök, ha a discrimináns pozitív vagy zérus, azaz

\begin{matrix} b + 2 - a^{2} \geq 0, ill. b \geq a^{2} - 2. \end{matrix}

(5)

Ezen feltétel azt jelenti, hogy a

P

pont a

\begin{matrix} b = a^{2} - 2 \end{matrix}

parabolán, ill. ezen belül tartozik feküdni.
Másrészt, a (4) egyenlet gyökei:

\begin{matrix} z_{1} = \frac{a + \sqrt[]{b + 2 - a^{2}}}{2} és z_{2} = \frac{a - \sqrt[]{b + 2 - a^{2}}}{2} . \end{matrix}

Ezek a köv. feltételeket kell, hogy kielégítsék:

\begin{matrix} - 2 \leq a + \sqrt[]{b + 2 - a^{2}} \leq 2 \end{matrix}

(6)

és

\begin{matrix} - 2 \leq a - \sqrt[]{b + 2 - a^{2}} \leq 2. \end{matrix}

(7)

Az (1)-ből következik, hogy

\begin{matrix} - 2 \leq a \leq + 2. \end{matrix}

Ezért a (6) kettős feltétel baloldali, a (7) jobboldali része ki van elégítve. Ha

a > 0

, akkor (6)-ból

\begin{matrix} a + \sqrt[]{b + 2 - a^{2}} \leq 2, \end{matrix}

azaz

\begin{matrix} b \leq 2 {(a - 1)}^{2} . \end{matrix}

(6a)

a < 0

, akkor (7)-ből

\begin{matrix} - 2 \leq a - \sqrt[]{b + 2 - a^{2}}, \end{matrix}

azaz

\begin{matrix} b \leq 2 {(a + 1)}^{2} . \end{matrix}

(7a)

P

pontnak a

\begin{matrix} b = 2 {(a - 1)}^{2} és b = 2 {(a + 1)}^{2}, \end{matrix}

továbbá a

\begin{matrix} b = a^{2} - 2 \end{matrix}

görbék által határolt síkrészben kell feküdnie.

II.

1^{0}

A O P ▵ \sim B O P' ▵

, mert mindkettő derékszögű és

A O P ∢ = B O P' ∢

.
Ezért

\begin{matrix} \frac{O P}{O P'} = \frac{O A}{O B} . \end{matrix}

Ebből pedig következik az összes

O P M P'

derékszögű négyszögek hasonlósága.

2^{0}

. Minthogy az

M

pont az egymásra merőleges

A P

és

P' B

egyenesek metszőpontja,

A M B ∢ = 90^{\circ}

, tehát az

M

pont mértani helye az

A B

átmérő fölött leírt kör.

3^{0}

. A

k_{a}

és

k_{b}

körök második közös pontja az

A B

átfogó

C

pontja, t. i. az

A O B ▵

-ben az

A B

átfogóra bocsátott magasság talppontja. Az

1^{0}

-ből következik, hogy az összes

P O P' ▵

-ek hasonlóak:

P O P' ▵ \sim A O B ▵

, tehát az

O P P' ∢ = O A B ∢ \equiv O A C ∢

. Ezek mindegyike a

k_{a}

kör kerületi szöge; ezen szögekhez tartozó ív egyik végpontja

O

közös, kell tehát, hogy a másik végpontja, a

C

is közös legyen. A

P P'

eszerint mindig a

C

szilárd ponton megy keresztül. ¹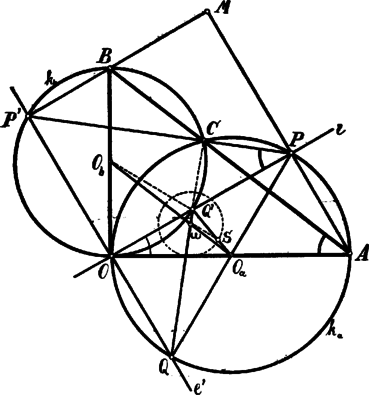

4^{0}

. Az

1^{0}

-ből következik, hogy

\begin{matrix} O Q Q' ▵ \sim O P P' ▵; \end{matrix}

ha az

O Q Q' ▵

-t

90^{\circ}

-kal elforgatjuk, úgy, hogy derékszöge az

O P P' ▵

derékszögével összeesik, akkor az új helyzetben

Q Q'

párhuzamos lesz

P P'

-vel; a

90^{\circ}

-os elforgatás előtt tehát

Q Q' ⊥ P P'

. ²

5^{0}

. A

P Q Q' ▵

-nek

P Q

oldala mindig keresztül megy a

k_{a}

kör

O_{a}

középpontján ³, azaz

P Q

felezőpontja a szilárd

O_{a}

pont. A

P Q Q' ▵

S

súlypontja eszerint mindig az

O_{a} Q'

súlyvonalon fekszik, úgy, hogy

\begin{matrix} O_{a} S = \frac{O_{a} Q'}{3} . \end{matrix}

Ha tehát a

Q'

leírja a

k_{b}

kört, akkor az

S

pont is egy

k

kört ír le. ⁴

¹Ha a

P

pont a

k_{a}

körnek az

O A B ▵

-ön belül fekvő

O C

ívére esnék, akkor

O P C ∢ = 180^{\circ} - A O C ∢ = 180^{\circ} - O P P' ∢

; az állítás ebben az esetben is igaz marad.

² $Q Q'$ is keresztülmegy a $C$ ponton.

³ $P Q$ egyszersmint a $k_{a}$ körbe írt $P O Q$ derékszögű háromszögnek az átfogója.

⁴Az $O_{a}$ pont ezen $k$ körnek és $k_{b}$ -nek külső hasonlósági pontja. A $k$ középpontja az $O_{a} O_{b}$ egyenesen fekszik.