Kezdőlap


Cím:	1927. A XXXI. Eötvös Loránd matematikai tanulóverseny - 2.
Szerző(k):	Dénes György , Hajós György , Jónás Pál , Petrovits Gábor , Somogyi László , Székely Lilly
Füzet:	1928/január, 145. oldal	PDF \| MathML
Témakör(ök):	Kürschák József (korábban Eötvös Loránd)

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

311. Legyenek $a$ , $b$ , $c$ olyan egész számok, melyek az

\begin{matrix} m = a d - b c \end{matrix}

számhoz viszonylagos törzsszámok. Bebizonyítandó, hogy azok az egész számokból álló (

x

y

) számpórok, amelyekre

a x + b y

osztható

m

-mel, ugyanazok, mint amelyekre

c x + d y

osztható

m

-mel.

I. Megoldás. Kiindulunk abból, hogy a

\begin{matrix} c (a x + b y) - a (c x + d y) = b c y - a d y = m y \end{matrix}

(1)

összefüggés minden (

x

y

) érték pár mellett fennáll. Ha tehát valamely (

x

y

) érték párral

a x + b y

osztható

m

-mel, akkor az

a (c x + d y)

szorzat is osztható vele; de

a

és

m

relatív prímszámok, tehát kell, hogy

c x + d y

legyen

m

-mel osztható. Megfordítva: amely (

x

y

) érték párokra

c x + d y

osztható

m

-mel, ugyanazokra

a x + b y

is osztható vele, mert

c

és

m

relatív priorszámok.
Ugyanerre az eredményre jutunk, ha a

\begin{matrix} - d (a x + b y) + b (c x + d y) = (b c - a d) x = m x \end{matrix}

összefüggésből indulunk ki.

Jónás Pál (Zrínyi Miklós rg. VII. o. Bp. VII.)

II. Megoldás. Az adott feltétel alapján kimondhatjuk, hogy a és b viszonylagos törzsszámok: ha ugyanis volna közös osztójuk, akkor ez osztaná az

m = a d - b c

számot is, tehát

a

és

m

, ill.

b

és

m

nem volnának rel. prímszámok. Ugyanígy

c

és

d

is viszonylagos törzsszámok. Ebből következik, hogy az

\begin{matrix} a x + b y = u (a d - b c) \end{matrix}

(1)

és

\begin{matrix} c x + d y = v (a d - b c) \end{matrix}

(2)

egyenletek mindegyikének vannak egész számú megoldásai.
A határozatlan egyenletek megoldásának ismert módszerét alkalmazva, az (1) egyenletet

\begin{matrix} x = u d - b v, y = a v - u c \end{matrix}

számpárok elégítik ki, ahol

u

és

v

tetszőleges egész számok. Azonban ezen értékpárok a (2) egyenletet is kielégítik, mert

\begin{matrix} c x + d y = c (u d - b v) + d (a v - u c) = v (a d - b c) . \end{matrix}

Tehát amely (

x

y

) értékpároknál

a x + b y

osztható

m

-mel, azoknál

c x + d y

is osztható vele és megfordítva.

Petrovics Gábor (Toldy Ferenc Főreál VIII. o. Bp. II.)

312. Mekkora mindazon négy jegyű számok összege, amelyek csak az

1

2

3

4

5

számjegyeket és pedig mindegyiket legfeljebb egyszer tartalmazzák?

Megoldás. Az

1

2

3

4

5

számjegyek mindegyike annyiszor áll valamely helyen, ahány ismétlés nélküli harmadosztályú variációt lehet képezni a többi négy elemből, tehát

4 \cdot 3 \cdot 2 = 24

-szer. Eszerint az egyesek összege:

\begin{matrix} 24 (1 + 2 + 3 + 4 + 5) = 360. \end{matrix}

De ugyanennyi a tízesek, a százasok és az ezresek összege is; tehát a szóban forgó

120

szám összege:

\begin{matrix} 360 \cdot 10^{3} + 360 \cdot 10^{2} + 360 \cdot 10 + 360 = 360 \cdot 1111 = 399 . 960. \end{matrix}

Somogyi László (premontrei gimn. VIII. o. Szombathely.)

313. Tekintsük az

A B C ▵

oldalait érintő 2 kör közül azt a kettőt, amely az

A B

oldalt

A

és

B

közölt érinti. Bebizonyítandó, hogy e két kőr sugarának geometriai közepe nem lehet nagyobb

\bar{A B}

felénél.

I. Megoldás. Legyen az

A B C ▵

-be beírt kör középpontja

I

, érintési pontja a

B C

oldalon

K

; a szóban forgó hozzáírt kör középpontja

I_{1}

, érintési pontja a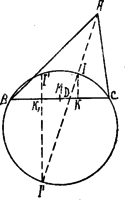

B C

oldalon

K_{1}

B

C

I

I_{1}

, pontok oly körön feküsznek, melynek átmérője

I I_{1}

; ugyanis a

B I

belső és

B I_{1}

külső szögfelezők egymásra merőlegesek, hasonlóképen

C I

és

C I_{1}

is.¹ Másrészt a

K

és

K_{1}

pontok ‐ a 294. sz. feladat szerint (l. IV. évf, 3. sz.) ‐ a

B C

oldal

M

felezőpontjától egyenlő távolságban vannak; ha tehát

K_{1}

pontban

B C

-re merőlegest állítunk, amíg az előbb említett kört

I'

pontban metszi, akkor

I' K_{1} = I K = ϱ

és

I_{1} K_{1} = ϱ_{a}

. Már most az egy ponton átmenő húrok szeleteire vonatkozó törvény szerint:

\begin{matrix} ϱ ϱ_{a} = \bar{I' K_{1}} \cdot \bar{K_{1} I_{1}} = \bar{B K_{1}} \cdot \bar{K_{1} C} . \end{matrix}

K_{1}

pont a

B C

oldalt két részre osztja. Ha egy távolságot (egy számot) két részre oszlunk, a részek szorzatának maximumát akkor kapjuk, ha a két rész egyenlő, azaz

\begin{matrix} ϱ ϱ_{a} = {\bar{B K}}_{1} \cdot \bar{K_{1} C} ≦ {(\frac{B C}{2})}^{2} vagyis \sqrt[]{ϱ ϱ_{a}} ≦ \frac{B C}{2} . \end{matrix}

Hajós György (Kegyesrendi gimn. VII. o. Bp.)

II. Megoldás. Ha az

I I'

szögfelező

B C

-t

D

pontban metszi, akkor ‐ az előbb idézett tétel értelmében:

\bar{I D} \cdot \bar{I' D} = \bar{B D} \cdot \bar{D C}

.
Azonban

I D ≧ ϱ

és

I' D ≧ ϱ_{a}

, tehát

ϱ ϱ_{a} ≦ \bar{B D} \cdot \bar{D C} ≦ {(\frac{B C}{2})}^{2}

Dénes György (áll. főreál. VII. o. Szombathely.)

III. Megoldás. Ismeretes képletek:

ϱ = \frac{t}{s}

és

ϱ_{a} = \frac{t}{s - a}

\begin{matrix} ϱ ϱ_{a} = \frac{t^{2}}{s (s - a)} = \frac{s (s - a) (s - b) (s - c)}{s (s - a)} = (s - b) (s - c) . \end{matrix}

s - b

és

s - c

tényezők ősszege:

2 s - (b + c) = a

, azaz állandó; tehát szorzatuk maximum, ha a tényezők egyenlők, azaz ha

\begin{matrix} s - b = s - c = \frac{a}{2} . \end{matrix}

Eszerint:

\begin{matrix} ϱ ϱ_{a} = (s - b) (s - c) ≦ {(\frac{a}{2})}^{2} vagyis \sqrt[]{ϱ ϱ_{a}} ≦ \frac{a}{2} . \end{matrix}

Székely Lilly (izr. leánygimn. VIII. o. Bp.)

¹L. még a 306. feladatban. (IV. évl, 4. sz.)