|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. Megoldások
201. Bebizonyítandó, hogy bárhogyan választjuk az ,,'' és ,,'' egész számokat, az
egyenletrendszernek mindig van egész számokból álló megoldása.
I. Megoldás. Legyen
Ha , , , egész számok, akkor , , , is azok. Ezen új ismeretlenekkel egyenletrendszerünk így alakul:
Ha páros szám, is páros szám tartozik lenni. Ezt pedig elérjük, ha az (1) alapján
) Ha páratlan, akkor (2) szerint is páratlan szám tartozik lenni, tehát, ha (1) alapján
Mindkét esetben páros szám lesz és így egyenletnek mindig van egész számú megoldása.
| Hajós György (kegyesrendi fg. VI. o. Bp.) |
II. Megoldás. Az első egyenletből Helyettesítsük ezt a másodikba; összevonás után: A legkisebb együtthatóval bíró ismeretlent fejezzük ki:
és ebből Ha , egész számok, akkor , és (1) alapján is egész számok, amelyek az adott egyenletrendszert kielégítik.
Minthogy a 4 ismeretlen között két összefüggés van megadva, két ismeretlen ‐ , ‐ értéke szabadon választható. Tekintettel arra, hogy a (2) egyenletben , , együtthatói relatív prímszámok, előre volt jelezhető, hogy a (2) egyenletnek és így a megadott egyenletrendszernek is ‐ az adott feltétel mellett ‐ mindig van egész számú megoldása.
| Weisz Sándor (debreceni főreál VIII. o.) |
III. Megoldás. Legyen és . Akkor az egyenletrendszernek egy megoldása ‐ amiről helyettesítéssel meggyőződhetünk ‐: Ha ezen értékeket -val szorozzuk, akkor az így nyert számok, tehát kielégítik az | |
egyenletrendszert. Viszont, ha és , akkor az egyenletrendszernek egy megoldása: Szorozzuk ezen értékeket -vel; akkor az így előálló értékek kielégítik ezen egyenletrendszert: | |
Ennélfogva az adott egyenletrendszernek egyik egész számú megoldása az I. és II. speciális esetek megoldásainak összegéből alakul:
202. Bebizonyítandó, hogy négy egymásután következő pozitív egész szám szorzata nem lehet egész számnak négyzete.
Megoldás. Ha a négy egymásután következő egész szám akkor szorzatuk (133. gyak. III. évf. 1. sz.) | |
azaz | |
Eszerint a négy szám szorzata két egymásután következő négyzetszám között van és így nem lehet négyzetszám.
| Némethy László (Szent Benedekrendi gimn. VIII. o. Győr) |
203. Egy kör kétszer akkora sugarú körön gördül, ennek belsejében. Milyen pályát ír le a gördülő kör kerületének valamely pontja?
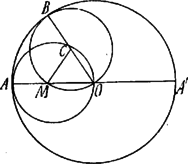
I. Megoldás. Induljunk ki abból a helyzetből, amidőn a gördülő kör pontja a nagyobbik körön van; a gördülő kör tetszőleges helyzetében ezután a középpontja -ben van és az kerületi pontja -be kerül, és ekkor kerületi pont van a nagy körön. Ekkor tehát a és ívek egyenlők; a hozzájuk tartozó középponti szögek pedig a sugarakkal fordítva arányosak, tehát .
Kössük össze -t -mel. A a egyenlőszárú háromszög külső szöge és így | |
azaz pont az egyenesen fekszik. Eszerint a gördülő kör kerületi pontja leírja az átmérőt, még pedig oda és vissza, mialatt az pont eredeti helyzetébe kerül.
| Mischung Ilona (szegedi leánygimn. VIII. o.) |
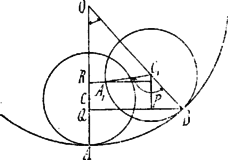
II. Megoldás. A sugarú kör az sugarú kör belsejében gördül. Amikor középpont -ben van, pont kerül -be és így hosszúságra nézve. Legyen és . Akkor az egyenlő hosszúságú íveknek megfelelő szögek a két körben a sugarakkal fordítva arányosak:
Az pont távolsága az egyenestől . Minthogy , és a -ben , továbbá pont távolsága -től , azért | |
Az adott esetben: és ezért . | |
Ez tehát annyit jelent, hogy pont az egyenesen fekszik.
| Hallóssy Zoltán (ciszterci rg. VIII. o. Bp.) |
Ezen dolgozatot, a Mathematikai és Physikai Társulat elnöksége engedélyével, a verseny színhelyén készítette. |
 PDF | MathML
PDF | MathML