Kezdőlap


Cím:	Tételek és feladatok a vectorgeometriából 3.
Szerző(k):	Dr. Bozóky Endre
Füzet:	1905/december, 79 - 89. oldal	PDF \| MathML
Témakör(ök):	Szakmai cikkek

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

$9$ . Vonaldarab közepe. A vonaldarab $A, B$ végpontjait a tetszésszerinti $O$ pontból hozzájuk vont $O A = A$ és $O B = B$ vectorokkal adván meg, a vonaldarab $M$ közepét az $O M = \frac{A + B}{2}$ vector határozza meg.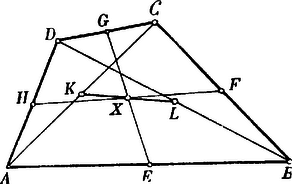

10

. Egy a síkban vagy a térben fekvő négyszög szemköztes oldalainak közepeit összekötvén, a nyert transversálisok egymást felezik. Metszéspontjuk annak a, vonaldarabnak közepe, mely az átlók közepeit köti össze.

A, B, C, D

pontokat egy tetszésszerinti

O

kezdőpontra vonatkoztatván a megfelelő vectorok

O A = A, O B = B, O C = C

és

O D = D

.
Ennélfogva

E

-nek

\frac{A + B}{2}

G

-nek

\frac{C + D}{2}

a vectoruk.

E G

közepének vectora

\begin{matrix} \frac{1}{2} (\frac{A + B}{2} + \frac{C + D}{2}) = \frac{A + B + C + E}{4} \end{matrix}

Hasonlóképpen

F

-nek

\frac{B + C}{2}

H

-nak

\frac{A + D}{2}

a vectoruk, s így

F H

közepének vectora

\begin{matrix} \frac{1}{2} (\frac{B + C}{2} + \frac{A + D}{2}) = \frac{A + B + C + D}{4} \end{matrix}

Ezzel a tétel első része igazoltatott.

K

-nak

\frac{A + C}{2}

L

-nek

\frac{B + D}{2}

a vectoruk s így

K L

közepének vectora

\begin{matrix} \frac{1}{2} (\frac{A + C}{2} + \frac{B + D}{2}) = \frac{A + B + C + D}{4} \end{matrix}

s így

E G, F H

és

K L

közepei egy pontba esvén össze, a tétel második része is be van bizonyítva.

11

. Az

O A B C

parallelogrammában tetszésszerint fölvett

D

ponton át az oldalokkal párhuzamos

E F, G H

egyeneseket húzunk. Bebizonyítandó, hogy az

O C, E H

és

G P

diagonálisok egyazon

I

ponton mennek keresztül.
Legyen

\begin{matrix} O A = A, tehát O G = m \cdot A \end{matrix}

\begin{matrix} O B = B, " O E = n \cdot B \end{matrix}

Az összeg értelmezése szerint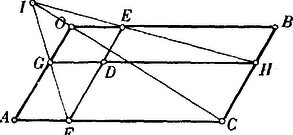

\begin{matrix} O G + G I = O I \end{matrix}

\begin{matrix} O G + x \cdot G F = y \cdot O C \end{matrix}

\begin{matrix} m A + x \cdot (G A + A F) = y \cdot (O A + A C) \end{matrix}

\begin{matrix} m \cdot A + x \cdot {(O A - O G + O E}) = y \cdot (O A + O B) \end{matrix}

az értékek további helyettesítése után:

\begin{matrix} m A + x (A - m A + n B) = y (A + B) \end{matrix}

honnét

\begin{matrix} {m + (1 - m) x - y} A + (n x - y) \cdot B = 0 \end{matrix}

s így

\begin{matrix} m + (1 - m) x - y = 0 \end{matrix}

\begin{matrix} n x - y = 0 \end{matrix}

mely egyenletrendszerből

\begin{matrix} x = \frac{m}{m + n - 1}, y = \frac{m n}{m + n - 1} . \end{matrix}

Az utóbbi kifejezés

m

és

n

-re vonatkozólag symmetrikus, ha tehát

I

-t mint

O C

és

E H

metszéspontját határozzuk meg, akkor is ugyanerre az eredményre kell jutnunk. Ezzel a tétel igazolást nyert.

\begin{matrix} I O = y \cdot C O \end{matrix}

\begin{matrix} I C = I O - C O = (y - 1) \cdot O C \end{matrix}

innét

\begin{matrix} \frac{I O}{I C} = \frac{y}{y - 1} = \frac{m n}{(1 - m) \cdot (1 - m n)} \end{matrix}

m

és

n

számok értelme szerint az

\frac{I O}{I C}

arány egyenlő az

O A B C

és

O G D E

parallelogrammák területeinek arányával.

12

. A teljes négyszög három átlójának közepei egyazon egyenesben fekszenek.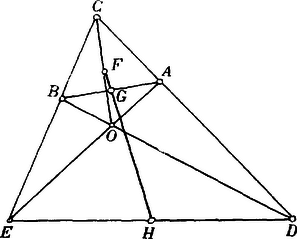

Legyen

\begin{matrix} O A = A, O E = m A \end{matrix}

\begin{matrix} O B = B, O D = n B \end{matrix}

akkor

\begin{matrix} O C = O A + A C = O A + x \cdot A D \end{matrix}

\begin{matrix} O C = O B + B C = O B + y \cdot B E \end{matrix}

ezekből

\begin{matrix} O A + x \cdot A D = O B + y \cdot B E \end{matrix}

\begin{matrix} O A + x (O D - O A) = O B + y \cdot (O E - O B) \end{matrix}

\begin{matrix} A + x (n B - A) = B + y \cdot (m A - B) \end{matrix}

\begin{matrix} (1 - x) A + n x B = (1 - y) B + m y A \end{matrix}

s így

\begin{matrix} 1 - x = m y \end{matrix}

\begin{matrix} 1 - y = n x \end{matrix}

mely egyenletrendszerből

\begin{matrix} x = \frac{m - 1}{m n - 1}, y = \frac{n - 1}{m n - 1} . \end{matrix}

Számítás közben kitűnt, hogy

\begin{matrix} O C = A + x \cdot (n B - A) \end{matrix}

s így

x

értékének helyettesítése, s a kifejezés kellő rendezése után

\begin{matrix} O C = \frac{m (n - 1)}{(m n - 1)} \cdot A + \frac{n (m - 1)}{m n - 1} \cdot B \end{matrix}

Minthogy:

\begin{matrix} O F = \frac{1}{2} O C = \frac{1}{2 (m n - 1)} {m (n - 1) A + n (m - 1) \cdot B} \end{matrix}

\begin{matrix} O G = \frac{1}{2} (A - B) \end{matrix}

\begin{matrix} O H = \frac{1}{2} (O E + O D) = \frac{1}{2} (m A + n B), \end{matrix}

most már

F G

és

G H

meghatározására kerülhet a sor.

\begin{matrix} O F + F G + G O = 0 \end{matrix}

\begin{matrix} F G = O G - O F = \frac{1}{2} (A + B) - \frac{1}{2 (m n - 1)} {m (n - 1) A + n (m - 1) B} = \end{matrix}

\begin{matrix} = \frac{1}{2 (m n - 1)} {(m - 1) A + (n - 1) B} \end{matrix}

\begin{matrix} O G + G H + H O = 0 \end{matrix}

\begin{matrix} G H = O H - O G = \frac{1}{2} (m A + n B - \frac{1}{2} {A + B) = \frac{1}{2} {(m - 1) A + (n - 1) \cdot B} \end{matrix}

E szerint

\begin{matrix} G H = (m n - 1) F G \end{matrix}

ami azt jelenti, hogy az

F, G, H

pontok egyugyanazon egyenesen fekszenek.

13

. Complanar vectorok. A vectorok összeadásának értelmezése szerint világos, hogy egy tetszésszerinti zárt polygon oldalait vectorokul tekintvén, azok összege zérus.
Alkalmazzuk a vectorpolygon ezen tételét három egyazon síkban fekvő, tehát complanar vectorra. Ha ezek

A, B

és

C

, akkor bebizonyíthatjuk, hogy

a, b, c

-vel algebrai számokat jelölvén, ezek mindig eleget tesznek az

\begin{matrix} a A + b B + c C = 0 \end{matrix}

egyenletnek.
Ugyanis a vectorok síkjában, vagy más, de ezzel párhuzamos síkban mindig szerkeszthetünk oly háromszöget, amelynek oldalai rendre párhuzamosak az

A, B, C

vectorokkal, s ennek a háromszögnek kerületi összege

\begin{matrix} a A + b B + c C . \end{matrix}

A complanar vectorok föltételi egyenlete csakis egy módon elégíthető ki.
Mert ha egyúttal

\begin{matrix} a' A + b' B + c' C = 0 \end{matrix}

is állana, akkor

C

-nek kiküszöbölése után

\begin{matrix} \frac{a}{c} A + \frac{b}{c} B = \frac{a'}{c'} A + \frac{b'}{c'} B \end{matrix}

következik, s ebből

\begin{matrix} \frac{a}{c} = \frac{a'}{c'}, \frac{b}{c} = \frac{b'}{c'} \end{matrix}

más szóval

\begin{matrix} a : a' = b : b' = c : c' \end{matrix}

s így az

a, b, c

-vel arányos

a', b', c'

számok nem tekinthetők önálló értékrendszernek.
Ezek szerint, ha

A, B, C

complanarvectorok, akkor

\begin{matrix} a A + b B + c C = 0; \end{matrix}

és viszont, ha ez a föltétel fennáll, akkor az

A, B, C

vectorok complanarok.
Ellenben, ha

A, B, C

nem complanar, hanem tetszésszerinti vectorok, akkor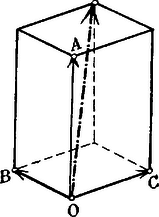

\begin{matrix} a A + b B + c C \end{matrix}

nem lehet zérus, mert annak a parallelepipedonnak átlójával egyenlő, amelyet az

A, B, C

vectorokkal párhuzamos élekből szerkeszthetünk. Ez a diagonális mindaddig nem lehet zérus, amíg a parallelepipedon három éle rendre zérussá nem válik.

Ha tehát valamely feladat tárgyalásánál arra az eredményre jutunk, hogy az általános helyzetű

A, B, C

vectorokra nézve

\begin{matrix} a A + b B + c C = 0 \end{matrix}

áll fenn, minthogy a kérdéses vectorokról tudjuk, hogy nem complanarok, kell, hogy

\begin{matrix} a = 0, b = 0, c = 0 \end{matrix}

álljon.
Viszont, ha azt találnók, hogy

\begin{matrix} a A + b B + c C = 0 \end{matrix}

de másrészt tudjuk, hogy

a, b, c

a zérustól különböző számok, akkor ebből az

A, B, C

vectorok complanar voltára kell következtetnünk.
Ezek az eredmények gyakorlatilag nagyfontosságúak. Első sorban arra használhatjuk fel, hogy a vectort új, sokszor előnyösen alkalmazható alakban állítsuk elő.
Ha

A

és

B

az adott

X

vectorral complanar, akkor

\begin{matrix} a A + b B + x X = 0 \end{matrix}

honnét

\begin{matrix} - x X = a A + b B \end{matrix}

vagy

(- x)

-szel osztván:

\begin{matrix} X = a' A + b' B \end{matrix}

A, B, C

nem complanar vectorok, akkor az

X

vector mindig

a A + b B + c C

alakban állítható elő; mert egyebet sem kell tennünk, mint az

A, B, C

vectorokkal párhuzamos élű olyan parallelepipedont szerkeszteni, melynek az élek közös csúcspontjából kiinduló átlója

= X

.
Az első eset a vectornak két, adott irányú complanar összetevőkre való szétbontását, a második eset pedig a vectornak három adott irányú összetevőre való szétbontását szolgáltatja.

14

. Annak föltétele, hogy három complanar vector végpontjai egyazon egyenesben feküdjenek.
Legyenek

A, B, C

az adott complanar vectorok, és

O

a közös kezdőpont. Tehát

\begin{matrix} A = O A, B = O B, C = O C . \end{matrix}

Ha az

A, B, C

pontok egyazon egyenesben fekszenek, akkor

\begin{matrix} A B = x \cdot A C \end{matrix}

s így

\begin{matrix} B - A = x \end{matrix}

Ezt a föltéleli egyenletet egybevetvén a complanarság föltételeivel

\begin{matrix} a + b + c = 0 \end{matrix}

s így azt mondhatjuk, hogy az

A, B, C

complanar vectorok végpontjai akkor fekszenek egyazon egyenesben, ha

a + b + c = 0

15

. Annak föltétele, hogy négy pont egyazon síkban feküdjék.
Legyenek

A, B, C, D

az adott pontok; hogy egyazon síkban feküdjenek, annak föltétele az, hogy az

A B, A C, A D

vectorok complanarok legyenek, tehát kielégítsenek egy

\begin{matrix} l \cdot A B + m \cdot A C + n \cdot A D = 0 \end{matrix}

alakú föltételi egyenletet.
A vectorokat az

O

kezdőpontra vonatkoztatván

\begin{matrix} l (B - A) + m (C - A) + n (D - A) = 0 \end{matrix}

honnét

\begin{matrix} - (l + m + n) A + l B + m (C + n D) = 0 \end{matrix}

következik.
Itt ismét azt látjuk, hogy az együtthatók összege zérus. Általában tehát négy pont akkor fekszik egyazon síkban, ha

\begin{matrix} a A + b B + c C + d D = 0 \end{matrix}

\begin{matrix} a + b + c + d = 0 \end{matrix}

együttesen állanak fenn.
Ha azt akarjuk kifejezni, hogy az

A

pont benne fekszik a

B C D

síkban, akkor

\begin{matrix} A = p B + q C + r D \end{matrix}

\begin{matrix} p + q + r = 1 \end{matrix}

föltételi egyenletek álljanak.

16

. Az

A B C

háromszögön belül fölvett tetszésszerinti

G

pontot összekötjük a háromszög csúcspontjaival. Keressük azt az összefüggést, mely az összekötő vectorok meghosszabbításai következtében a háromszög oldalain keletkező

6

vonaldarab közt fennáll.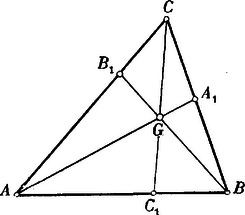

\begin{matrix} G A = a A \end{matrix}

\begin{matrix} G B = b B \end{matrix}

\begin{matrix} G C = c C \end{matrix}

complanar vectorok lévén

\begin{matrix} a A + b B + c C . \end{matrix}

Továbbá

\begin{matrix} G A_{1} = A_{1} = x A \end{matrix}

\begin{matrix} G B_{1} = B_{1} = y B \end{matrix}

\begin{matrix} G C_{1} = C_{1} = z C \end{matrix}

s így

\begin{matrix} A = \frac{A_{1}}{x}, B = \frac{B_{1}}{y}, C = \frac{C_{1}}{z} \end{matrix}

Ha a complanarság föntebbi föltételi egyenletébe

A

helyébe az

\frac{A_{1}}{x}

értéket helyettesítjük, akkor

\begin{matrix} \frac{a}{x} A_{1} + b B + c C = 0 \end{matrix}

azt fejezi ki, hogy az

A_{1} B C

vectorok is complanarok. De ezen vectorok

A_{1}, B, C

végpontjai ezenfelül egyazon egyenesben is fekszenek, tehát

\begin{matrix} \frac{a}{x} + b + c = 0 \end{matrix}

ugyanígy:

\begin{matrix} a + \frac{b}{y} + c = 0 \end{matrix}

\begin{matrix} a + b + \frac{c}{z} = 0 \end{matrix}

Ezen egyenletrendszerből

\begin{matrix} x = - \frac{a}{b + c} \end{matrix}

\begin{matrix} y = - \frac{b}{a + c} \end{matrix}

\begin{matrix} z = - \frac{c}{a + b} \end{matrix}

minélfogva

\begin{matrix} A_{1} = - \frac{a A}{b + c} \end{matrix}

\begin{matrix} B_{1} = - \frac{b B}{a + c} \end{matrix}

\begin{matrix} C_{1} = - \frac{c C}{a + b} \end{matrix}

vagy másképpen

\begin{matrix} A_{1} = - \frac{b B + c C}{b + c} \end{matrix}

\begin{matrix} B_{1} = - \frac{c C + a A}{a + c} \end{matrix}

\begin{matrix} C_{1} = - \frac{c A + b B}{a + b} \end{matrix}

Az utóbbi három egyenlet még így is írható:

\begin{matrix} b (A_{1} - B) = c (C - A_{1}) \end{matrix}

\begin{matrix} c (B_{1} - C) = a (A - B_{1}) \end{matrix}

\begin{matrix} a (C_{1} - A) = b (B - C_{1}) \end{matrix}

honnét

\begin{matrix} \frac{A_{1} - B}{C - A_{1}} = \frac{c}{b}, \frac{B_{1} - C}{A - B_{1}} = \frac{a}{c}, \frac{C_{1} - A}{B - C_{1}} = \frac{b}{a} \end{matrix}

vagy

\begin{matrix} \frac{B A_{1}}{A_{1} C} = \frac{c}{b}, \frac{C B_{1}}{B_{1} A} = \frac{a}{c}, \frac{A C_{1}}{C_{1} B} = \frac{b}{a} \end{matrix}

s így szorzatuk

\begin{matrix} \frac{B A_{1} \cdot C B_{1} \cdot A C_{1}}{A_{1} C \cdot B_{1} A \cdot C_{1} B} = 1 \end{matrix}

a keresett feltételi egyenlet, melyben Ceva tételére ismerünk.

17

. Collinear háromszögek. Ha azok az egyenesek, melyek két háromszögnek megfelelkező csúcspontjait kötik össze, egy pontban találkoznak, akkor a megfelelkező oldalak metszéspontjai egyazon egyenesben fekszenek.
Az ilyen háromszögeket collinearoknak hívjuk, a csúcspontokon átmenő transversálisok metszéspontja a collineatió centruma, a megfelelkező oldalok metszéspontjainak egyenese a collineatió tengelye.
A collineatió, mint általános geometriai rokonság minden speciálisabb jellegű rokonságot magában foglal.
Ha a collineatio centruma a végtelenben fekszik, tehát a collineatió sugarai párhuzamosak, akkor a rokonság átmegy az affinitásba.
Ha a collineatió tengelye a végtelenben fekszik, tehát a megfelelkező egyenesek párhuzamosak, akkor a hasonlóság, ha pedig mind a centrum, mind pedig a tengely a végtelenben vannak akkor az egybevágóság lép fel.
A vectorgeometria segítségével az előrebocsátott tételt következőképpen bizonyítjuk be.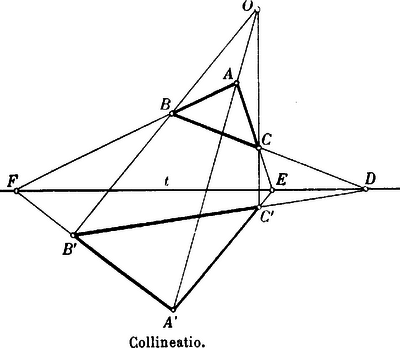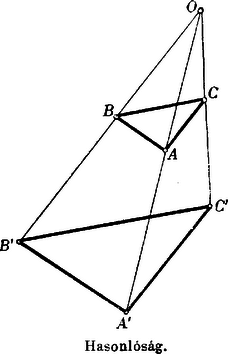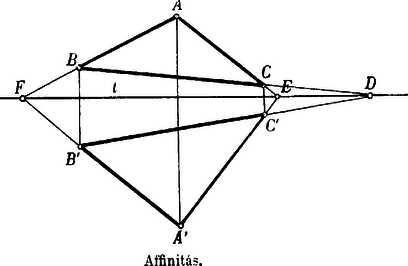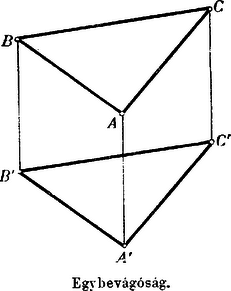

\begin{matrix} O A = A O A' = m A \end{matrix}

\begin{matrix} O B = B O B' = n B \end{matrix}

\begin{matrix} O C = C O C' = p C \end{matrix}

a collinear helyzet feltételei.

\begin{matrix} F = O F = O A + A F = O A + z \cdot B A = O A' + z' \cdot B' A' = \end{matrix}

\begin{matrix} = A + z \cdot B A = O A' + z' \cdot B' A' = \end{matrix}

\begin{matrix} = A + z (A - B) = m A + z' (m A - n B) \end{matrix}

innét

\begin{matrix} (1 + z) A - z B = m A + z' (m A - n B), \end{matrix}

tehát

\begin{matrix} 1 + z = m (1 + z') \end{matrix}

\begin{matrix} z = n z' \end{matrix}

honnét

\begin{matrix} z = \frac{(m - 1) n}{n - m} \end{matrix}

s így

\begin{matrix} F = (1 + \frac{(m - 1) n}{n - m}) A - \frac{(m - 1) n}{n - m} B \end{matrix}

\begin{matrix} F = \frac{- m (n - 1) A + n (m - 1) B}{n - m} \end{matrix}

\begin{matrix} D = \frac{- n (p - 1) A + p (n - 1) C}{n - p} \end{matrix}

\begin{matrix} E = \frac{- p (m - 1) C + m (p - 1) A}{p - m} \end{matrix}

\begin{matrix} f = (m - n) (p - 1) \end{matrix}

\begin{matrix} d = (n - p) (m - 1) \end{matrix}

\begin{matrix} e = (p - m) (n - 1) \end{matrix}

jelöléseket alkalmazunk, akkor

\begin{matrix} d D + e E + f F = 0 \end{matrix}

\begin{matrix} d + e + f = 0 \end{matrix}

azt mutatja, hogy

D, E

és

F

egyazon egyenesben fekszenek. Tényleg

\begin{matrix} d + e + f = m p - n p - m + n + m n - m p - n + p + p n - m n - p + m = 0. \end{matrix}