Kezdőlap


Cím:	Tételek és feladatok a vectorgeometriából 2.
Szerző(k):	Dr. Bozóky Endre
Füzet:	1905/november, 49 - 52. oldal	PDF \| MathML
Témakör(ök):	Szakmai cikkek

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

$3$ . Nem párhuzamos vectorok összeadása és kivonása. Az $A B$ és $B C$ vectorok összegéül azt az $A C$ vectort tekintjük, mely az $A B$ és $B C$ elmozdulásoktól alkotott parallelogrammának $A$ -tól kiinduló átlója.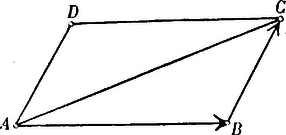

Ezen értelmezés alapján a vectorok összeadása commutatív művelet. Az összeg tensora azonban általában nem egyenlő a tagok tensorainak összegével.
A kivonás művelete ezzel szintén értelmezve van. Mert ha

\begin{matrix} A B + B C = A C \end{matrix}

akkor viszont

\begin{matrix} A C - A B = A C + B A \end{matrix}

\begin{matrix} = B A + A C = B C . \end{matrix}

Ezen értelmezéseinkkel minden vectortermészetű mennyiség (elmozdulás, sebesség, gyorsulás, erő, tengelynyomaték stb.) összetevése és szétbontása elintézést nyert.
Közvetlenül világos az is, hogy két különböző irányú vector különbsége sohasem lehet zérus.
Innét következik, hogy ha

A

és

B

különböző irányú vectorok közt az

m A + n B = 0

összefüggés áll fenn, hol

m

és

n

valós számokat jelentenek, akkor szükségképpen

m = 0

és

n = 0

. Ezt az eredményt kissé általánosíthatjuk.
Ha

\begin{matrix} m A + n B = p A + q B \end{matrix}

akkor

\begin{matrix} (m - p) A + (n - q) B = 0 \end{matrix}

s ez csak úgy állhat, ha

m = p

és

n = q

.
Eddigi ismereteinket már is felhasználhatjuk arra, hogy velük a gyakorlat terére lépjünk.

4

. A parallelogramma átlói felezik egymást.

A O = x \cdot A C

és

B O = y \cdot B D

tehető, s most már arra kell törekednünk, hogy az

x, y

ismeretleneket meghatározzuk.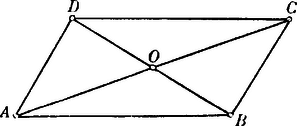

\begin{matrix} A O = A B + B O \end{matrix}

\begin{matrix} x \cdot A C = A B + y \cdot B D \end{matrix}

\begin{matrix} x \cdot (A B + B C) = A B + y \cdot (B C + C D) \end{matrix}

Tekintetbe véve, hogy

\begin{matrix} B C + C D = B C - D C = B C - A B \end{matrix}

tehát

\begin{matrix} x \cdot (A B + B C) = A B + y \cdot (B C - A B) \end{matrix}

\begin{matrix} (x + y - 1) \cdot A B + (x - y) \cdot B C = 0 \end{matrix}

honnét

\begin{matrix} x + y - 1 = 0 \end{matrix}

\begin{matrix} x - y = 0 \end{matrix}

mely egyenletrendszerből

x = y = \frac{1}{2}

. Így tényleg

A O = \frac{1}{2} A C

és

B O = \frac{1}{2} B C

5

. Az

A B C D

parallelogrammát

A B

-vel párhuzamosan

Q P

egyenessel metsszük. Bebizonyítandó, hogy

Q C

és

D P

-nek

S, A P

és

Q B

-nek

R

metszéspontjait egy a

B C

oldallal párhuzamos egyenes köti össze.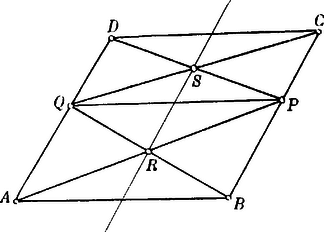

\begin{matrix} R S = Q S - Q R = \frac{1}{2} Q C - \frac{1}{2} Q B = \frac{1}{2} (Q C - Q B) \end{matrix}

De másrészt

\begin{matrix} Q B + B C = Q C \end{matrix}

honnét

\begin{matrix} B C = Q C - Q B . \end{matrix}

Így tehát

\begin{matrix} R S = \frac{1}{2} B C \end{matrix}

ami állításunkat igazolja. (Lásd:

2

. p.)

6

. Ha az

A B C D

parallelogramma

A B

oldalának

E

közepét

D

-vel összekötjük, akkor

E D

és

A C

egymást kölcsönösen a harmadrészükben metszik.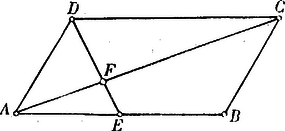

Legyen

\begin{matrix} A B = B, \end{matrix}

\begin{matrix} A D = D . \end{matrix}

Minthogy

\begin{matrix} A F = x \cdot A C = x (A B + B C) \end{matrix}

\begin{matrix} E F = A F - A E = y \cdot E D \end{matrix}

\begin{matrix} E F = x (A B + B C) - A E = y (A D - A E) \end{matrix}

\begin{matrix} x (B + D) - \frac{B}{2} = y (D - \frac{B}{2}) \end{matrix}

\begin{matrix} (x + \frac{y}{2} - \frac{1}{2}) B + (x - y) D = 0 \end{matrix}

innét

\begin{matrix} x + \frac{y}{2} - \frac{1}{2} = 0 \end{matrix}

\begin{matrix} x - y = 0 \end{matrix}

tehát

\begin{matrix} x = y = \frac{1}{3} \end{matrix}

ennélfogva

\begin{matrix} A F = \frac{1}{3} A C, \end{matrix}

\begin{matrix} E F = \frac{1}{3} E D . \end{matrix}

7

. A háromszög súlyvonalai egy pontban találkoznak, s a súlypont a csúcsoktól számítva a súlyvonalak

\frac{2}{3}

-ában fekszik.
Megállapodásaink szerint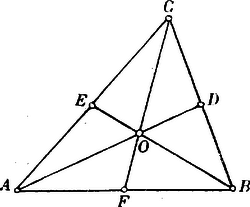

\begin{matrix} A B = B és A C = C \end{matrix}

jelölést használva

\begin{matrix} B C = A C - A B = C - B \end{matrix}

\begin{matrix} A E = \frac{1}{2} C \end{matrix}

\begin{matrix} A F = \frac{1}{2} B \end{matrix}

\begin{matrix} B D = \frac{1}{2} B C = \frac{1}{2} (C - B) . \end{matrix}

Ezen jelölések bevezetése után

\begin{matrix} A O = x \cdot A D = x \cdot (A B + B D) = \frac{x}{2} (B + C), \end{matrix}

\begin{matrix} B O = y \cdot B E = y \cdot (A E - A B) = y \cdot (\frac{C}{2} - B) \end{matrix}

Az összeadás értelmezése szerint

\begin{matrix} A O = A B + B O \end{matrix}

\begin{matrix} \frac{x}{2} \cdot (B + C) = B + y \cdot (\frac{C}{2} - B) \end{matrix}

\begin{matrix} (\frac{x}{2} + y - 1) B + \frac{x - y}{2} C = 0, \end{matrix}

honnét

\begin{matrix} \frac{x}{2} + y - 1 = 0 és x - y = 0, \end{matrix}

mely egyenletrendszerből

x = y = \frac{2}{3}

.
Így tehát

A O = \frac{2}{3} A D

és

B O = \frac{2}{3} B E

A D

és

C F

metszéspontja ugyanezt az eredményt adván, a három súlyvonal tényleg egy ponton megy át.

8

. Az

A B C

háromszögnek

A B, B C, C A

oldalait illetőlegesen

F, D, E

-ig az oldalak fél hosszúságával meghosszabbítván, határozzuk meg az

A D, B E, C F

egyenesek

G, H, K

metszéspontjait.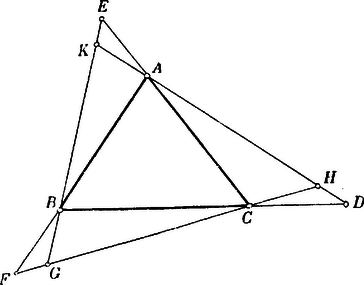

Legyen

\begin{matrix} B C = 2 A, C A = 2 B, \end{matrix}

akkor

\begin{matrix} B D = 3 A és C E = 3 B . \end{matrix}

\begin{matrix} B K = x \cdot B E = x \cdot (B C + C E) = x \cdot (2 A + 3 B) \end{matrix}

Másrészt

\begin{matrix} B K = B D + D K = B D + y \cdot D A = B D + y \cdot (C A - C D) = 3 A + y \cdot (2 B - A) \end{matrix}

Ezen két érték összehasonlítása alapján

\begin{matrix} x \cdot (2 A + 3 B) = 3 A + y \cdot (2 B - A) \end{matrix}

\begin{matrix} (2 x + y - 3) \cdot A + (3 x - 2 y) B = 0 \end{matrix}

honnét

\begin{matrix} 2 x + y - 3 = 0 \end{matrix}

\begin{matrix} 3 x - 2 y = 0 \end{matrix}

tehát

\begin{matrix} x = \frac{6}{7}, y = \frac{9}{7} . \end{matrix}

E szerint

\begin{matrix} B K = \frac{6}{7} B E \end{matrix}

\begin{matrix} E K = \frac{1}{7} E B \end{matrix}

\begin{matrix} F G = \frac{1}{7} F C \end{matrix}

\begin{matrix} D H = \frac{1}{7} D A . \end{matrix}

B E

-t adottnak vesszük, akkor az idomot

B

- és

E

-ből kiindulva megszerkesztvén,

B E

-nek

\frac{1}{7}

találhatjuk.