Az Apolloniusról elnevezett föladat általános alakjában így hangzik: Szerkesztendő olyan kör, mely három adott kört érint. Apollonius $200$ évvel élt K. e. Ő az érintési föladatokat kúpszeletek segítségével oldotta meg.
Viéte francia mathematikus $1600$-ban "Apollonius Gallus" című művében önállóan tárgyalta e föladatot. Viéte óta több kitűnő mathematikus foglalkozott e föladattal. Így többek között: Descartes, Newton, Lambert, Carnot, Gauss, Binet, Gergonne, Plücker, Poncelet, dr. Hunyadi Jenő stb.
A szerkesztéseknél minden lépten-nyomon egy-egy ily föladatra akadunk. Sok feladat végelemzésben ilyenre vezethető vissza.
Minthogy tankönyveink ezeket nem tárgyalják, a következőkben adjuk kimerítő tárgyalásukat.
A föladatnak általában nyolc megoldása lehet. Ez esetek föltüntetése végett oly köröket tekintünk csak, melyek egymást ne messék, ne érintsék és közülök egyik se feküdjék a másikban; mert e speciális esetekben a megoldások száma alábbszáll.
Az adott köröknek eme említett kölcsönös helyzeténél a keresett kör érintheti a három kört úgy, hogy

1.P,P,P;2.P,P,e;3.P,P,O;4.P,e,e;5.P,e,O;6.P,O,O;7.e,e,e;8.e,e,O;9.e,O,O;10.O,O,O.
Ám, az első és hetedik esettel nem kell külön foglalkoznunk, mert azonosak evvel a két föladattal; egy háromszög köré, illetőleg oly kört szerkeszteni, mely egy háromszög oldalait érinti; az utóbbinak négy megoldása van. A fennmaradó nyolc eset két csoportba osztható aszerint, amint az adatok között legalább egy pont fordul elő vagy egy sem.
Lássuk az eseteket sorra.

 

$I$.   Adva van két pont és egy egyenes. Keressük azt a kört, mely a pontokon átmenve az egyenest érinti.
Jelölje $A$ és $B$ az adott pontokat és e az adott egyenest. A keresett körnek húrja $AB$ és $e$ annak érintője. Legyen ezeknek közös pontja $C$ és $e$ egyenesen $F$ az érintési pont. A $C$ ponton áthaladó átszelő és érintő között a következő összefüggés érvényes: $CA\cdot CB={\overline{CF}}^2$, azaz $CF$ mértani középarányosa $CA$ és $CB$ szeleteknek.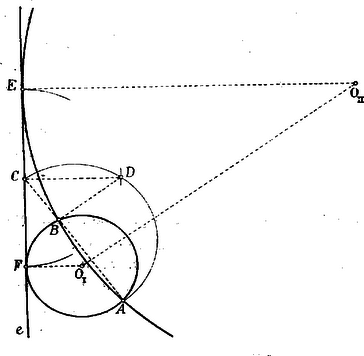

 

 

E középarányos szerkesztése végett $AC$ fölé félkört és $B$-ben $AC$-re merőlegest rajzolunk; ezek $D$ közös pontjának távolsága $C$-től a kívánt mértani középarányos. Ezt a közt $C$-től $e$-re mérjük $E$, illetőleg $F$-ig.
A keresett körök középpontjainak egyik mértani helye $AB$ köznek szimmetrálisa, a másik pedig $E$-ben, illetőleg $F$-ben $e$-re állított merőleges.

 

$II$.  Adva van két pont és egy kör. Keressük azt a kört, mely a pontokon átmegy és a kört érinti.
Legyenek az adott pontok $A$ és $B$ és a kör középpontja $O$. Vezessünk $A$ és $B$ pontokon át tetszőleges, az adottat $C$ és $D$ pontokban metsző kört és jelöljük $CD$ és $AB$ közös pontját $E$-ve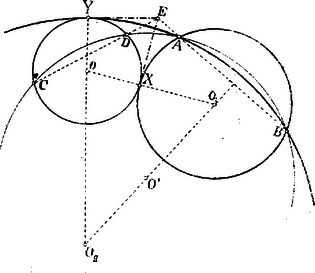l.

 

 

Legyen az adott körön $X$ az érintési pont; ekkor egyfelől:

$\begin{array}{c}{\displaystyle EB\cdot EA={\overline{EX}}^2\mathrm{,}}\end{array}$

másfelől:

$\begin{array}{c}{\displaystyle EC\cdot ED={\overline{EX}}^2\mathrm{.}}\end{array}$

Ez utóbbi egyenlet értelmében az adott körhöz $E$-ből érintőket rajzolunk, melyek az első egyenlet szerint a keresett körnek is érintői, miáltal az $X$ és $Y$ érintési pontokat kapjuk
A körök középpontjai egyrészt $AB$ köznek szimmetrálisán, másrészt az $XO$ és $YO$ egyeneseken feküsznek.

 

$III$.  Adva van egy pont és két egyenes. Keressük ama kör középpontját, mely a ponton átmegy és az egyeneseket érinti.
Legyenek a megadott elemek $A\mathrm{,}e$ és $e_1$. A keresett kör középpontjának egyik mértani helye az ($e\mathrm{,}{e}_1$) szög szimmetrálisa; ezért ez a kör $A$-nak $B$ szimmetriás pontpárján is át fog haladni.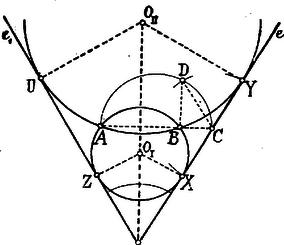

 

 

Ezzel e föladatot visszavezettük az $I\mathrm{.}$ esetre, melynél fogva oly kört kerestünk, mely $A$ és $B$ pontokon átmegy és az $e$ vagy $e_1$ egyenest érinti.

 

$IV$.  Adva van egy pont, egy egyenes és egy kör. Keressük ama kör középpontját, mely a ponton áthaladva az egyenest és a kört érinti.
Legyen $A$ az adott pont, $e$ az egyenes és $O$ a kör középpontja.
Tekintsük a föladatot megoldottnak és jelölje $O_1$ a keresett kör középpontját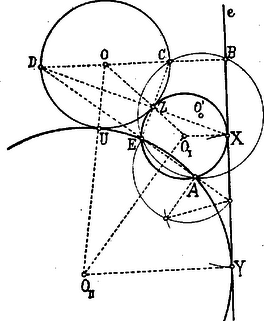

 

 

Emeljünk $O$-ból és $O_1$-ből merőlegeseket $e$-re; ezeknek talppontjai $B$ és $X$. Az $OD$ és $O_{1}X$ párhuzamos sugarak végső pontjainak $DX$ összekötő egyenese az adott és a keresett kör $Z$ belső hasonlósági pontján halad át.
A $BDX$ és $CDZ$ derékszögű háromszögek hasonlóságából következik, hogy:

$\begin{array}{c}{\displaystyle CD:DZ=DX:BD\mathrm{,}}\end{array}$

vagy:

$\begin{array}{c}{\displaystyle DC\cdot DB=DX\cdot DZ\mathrm{.}}\end{array}$

A $DA$ és $DX$ átszelőkön támadt szeletekre nézve érvényes hogy:

$\begin{array}{c}{\displaystyle DA\cdot DE=DX\cdot DZ;}\end{array}$

e két egyenlet összehasonlítása adja, hogy

$\begin{array}{c}{\displaystyle DC\cdot DB=DA\cdot DE\mathrm{,}}\end{array}$

azaz: $A\mathrm{,}B\mathrm{,}C$ pontok $E$ ponttal együtt egy kör kerületén feküsznek, mely kör $A\mathrm{,}B$ és $C$ pontok által meg van határozva, tehát $O\text{'}$ középpontja megszerkeszthető. E körön $AD$ egyenes az $E$ pontot megállapítja.
Így ezt a föladatot is visszavezettük az $I$. esetre, mely szerint oly kör szerkesztendő, mely $A$ és $E$ pontokon átmenve $e$ egyenest érinti. E köröknek középpontjai egyfelől az $AE$ köz szimmetrálisában, másfelől az $X$ és $Y$ érintési pontokon át $e$-re állított merőlegesekben feküsznek. Ha végül e középpontokat összekötjük $O$-val, nyerjük az adott körön az $U$ és $Z$ érintési pontokat.
A föladatnak még két megoldása van. Ugyanis: előállítjuk ama segédkört, mely most $A\mathrm{,}B$ és $D$ pontokon megy át és jelöljük középpontját $O\text{'}\text{'}$-vel; ezt a kört $AC$ egyenes messe $E\text{'}$ pontban. Végül ama körök középpontjait keressük, melyek $A$ és $E\text{'}$ pontokon mennek át és $e$-t érintik. Ezek a körök az adottat körülfogva érintik.

 

$V$.   Adva van egy pont és két kör, szerkesszük meg azt a kört, mely e ponton átmegy és a köröket érinti.
Jelölje $A$ az adott pontot, $O$ és $O_1$ a körök középpontjait. Legyen $O_I$ a keresett kör középpontja és $X\mathrm{,}Y$ az érintési pontok. E pontok összekötő egyenese az adott köröket $U\mathrm{,}Z$ pontokban és a centrálisukat $H$ pontban metszi.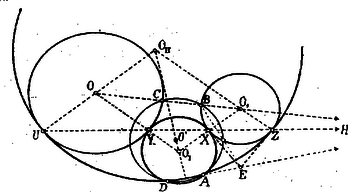

 

$\begin{array}{c}{\displaystyle OYU\sphericalangle =XY{O}_1\sphericalangle =O_{1}XY\sphericalangle =O_{1}XZ\sphericalangle =O_{1}ZX\sphericalangle ;}\end{array}$

ebből következik, hogy $OY\parallel O_{1}Z$ és hogy $H$ az adott körök külső hasonlósági pontja.
Ennélfogva:

$\begin{array}{c}{\displaystyle HX\cdot HY=HB\cdot HC;}\end{array}$

másfelől:

$\begin{array}{c}{\displaystyle HX\cdot HY=HA\cdot HD;}\end{array}$

e szerint:

$\begin{array}{c}{\displaystyle HB\cdot HC=HA\cdot HD;}\end{array}$

Ez az utolsó egyenlet azt mondja, hogy az $A\mathrm{,}B\mathrm{,}C$ és $D$ pontok egyugyanazon körön feküsznek, mely kört az $A\mathrm{,}B$ és $C$ pontok már megállapítják; középpontja $O\text{'}$ és rajta a $D$ pont is ismeretessé válik az $AH$ egyenes segítségével.
A föladat ezek után a $II$. esetre vezetett, mely szerint az a kör keresendő, mely átmegy az $A$ és $D$ pontokon és az adott körök valamelyikét érinti. Az ott megállapított szerkesztés folytán oly segédkör szükséges, mely az $A$ és $D$ pontokon áthaladva pl. $O_1$ középpontú kört messe. Ez a kör a jelen esetben a már fölhasznált $O\text{'}$ középpontú kör lehet. Az ennek segítségével nyert $E$ pontból $O_1$ körhöz rajzolt érintők az $X$ és $Z$ érintési pontokra vezetnek.
A keresett körök $O_I$ és $O_{II}$ középpontjainak egyik mértani helye az $AD$ köz szimmetrálisa, a másik az $O_{1}X$ és $O_{1}Z$, illetőleg $OU$ és $OY$ egyenesek. (Az egyik kör az adottakat kizárólag, a másik bezárólag érinti.) Ha ugyanezt a szerkesztést az adott körök belső hasonlósági pontjának figyelembevételével ismételjük, még két, a föltételeket kielégítő, kört nyerünk, melyek az adottak egyikét kizárólag, másikát körülfogva érintik. A föladatnak ezek szerint négy megoldása van.