Kezdőlap


Cím:	A háromszög területének egyik képletéről
Szerző(k):	Szabó Péter
Füzet:	1904/december, 71 - 77. oldal	PDF \| MathML
Témakör(ök):	Szakmai cikkek

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A geometria kézikönyvei a háromszög területének $(T)$ képletei között felsorolják a következőt is:

\begin{matrix} T = \sqrt[]{r r_{1} r_{2} r_{3} .} \end{matrix}

Azonban csak úgy szokták említeni, mint érdekes numerikus összefüggést a terület és a háromszög négy érintő körének sugarai között.
Talán nem felesleges az a megjegyzés, hogy ennek a képletnek geometriai értelmezés is adható, úgy hogy a levezetése is nagyobbára geometriai úton végezhető.
Ebben a közleményben ugyanis bebizonyítom a következő tételt:
Minden háromszöghöz szerkeszthető olyan négyszög:

1

. amelynek csúcsai a körülírt körre esnek és területe a háromszög területével egyenlő;

2

. a négyszögnek

a', b', c', d'

oldalaiból alakított

\begin{matrix} s' - a', s' - b', s' - c', s' - d' \end{matrix}

különbségek

(2 s' = a' + b' + c' + d')

sorra nem egyebek, mint az érintő körök sugarai:

\begin{matrix} r, r_{1}, r_{2}, r_{3} . \end{matrix}

Ennek a tételnek közvetlen következménye, hogy a négyszög területét az oldalakkal kifejezve, az elül említett képletet kapjuk. Tehát joggal mondhatjuk, hogy ez a tétel a mondott képletnek geometriai tartalmát adja meg.
A bebizonyításhoz szükséges segédtételeket előre bocsátom.

1

. A magassági pontnak a háromszög valamelyik csúcsától való távolsága kétszer akkora, mint a körülírt kör középpontjának távolsága a csúccsal szemben fekvő oldaltól.
Ha az

A B

oldal felező pontja

C_{2}

, körülírt kör középpontja

O

és a magassági pont

M

, azt kell megmutatni, hogy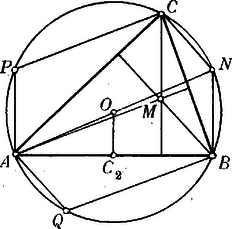

\begin{matrix} C M = 2 \cdot O C_{2} . \end{matrix}

E végből vonjuk (

1.

rajz)

\begin{matrix} B N ∥ C M, C N ∥ B M . \end{matrix}

C M B N

parallelogrammában:

\begin{matrix} B N = C M . \end{matrix}

(1)

Minthogy továbbá

B N C ∢ = C M B ∢ = 180^{\circ} - A ∢, N

pontja a körülírt körnek, de mivel még

N B ⊥ A B, A N

átmérő

(= 2 R)

, tehát az

O

ponton átmegy. Ezért

\begin{matrix} A O C_{2} Δ \sim A N B Δ, \end{matrix}

s a hasonlóság arányszáma

1 : 2

; a honnan következik, hogy

\begin{matrix} N B = 2 \cdot O C_{2}, \end{matrix}

vagy

(1)

-re való tekintettel

\begin{matrix} C M = 2 \cdot O C_{2} . \end{matrix}

(2')

Jelöljük rövidség kedvéért, a magassági pont távolságát az

A, B, C

csúcsoktól

m'_{1}, m'_{2}, m'_{3}

-vel, a körülírt kör középpontjának távolságát a szembenfekvő oldalaktól

x_{1}, x_{2}, x_{3}

-mal, akkor még írhatjuk:

\begin{matrix} m'_{1} = 2 x_{1}, m'_{2} = 2 x_{2}, m'_{3} = 2 x_{3} . \end{matrix}

(2)

Az előbbi bizonyítás hegyesszögű háromszögre vonatkozik, de tompaszögűre is változatlanul átvihető.

2

. Az

x_{1}, x_{2}, x_{3}

távolságok kifejezhetők a négy érintő kör sugaraival,

r, r_{1}, r_{2}, r_{3}

- mal.
Ez összefüggések geometriai levezetésére vonjuk meg az

A B C

háromszögben (2. rajz) pl. a

C

szög belső és külső szögfelezőit, melyek a körülírt kört

E

-ben és

F

-ben messék.

Legyenek az érintő körök középpontjai

O', O_{1}, O_{2}, O_{3}

; vetületeik az

A B

oldalon sorra

K', K_{1}, K_{2}, K_{3}

, a körülírt kör középpontja

O

, az

A B

oldal felezőpontja

C_{1}

.
Úgy, hogy

C E ⊥ C F

lévén,

E F

a körülírt kör átmérője:

O

-n keresztül megy; azonkívül a miatt, hogy

A F

ív

= F B

ív:

E F ⊥ A B

, tehát

C_{2}

is rajta van. Következőleg:

\begin{matrix} E F ∥ O' K' ∥ O_{1} K_{1} ∥ O_{2} K_{2} ∥ O_{3} K_{3} . \end{matrix}

Mindenekelőtt a

C_{2} E

távolságot fejezzük ki, mert

\begin{matrix} C_{2} E = R - x_{3} \end{matrix}

(3)

lévén, ezzel

x_{3}

-ra is nyertünk kifejezést. (Tompaszögű háromszögnél

(C ∢ > 90^{\circ}) x_{3}

-at negatív jellel kell venni.) Fontoljuk meg erre nézve, hogy

\begin{matrix} A K_{3} = B K', \end{matrix}

tehát még:

\begin{matrix} C_{2} K_{3} = C_{2} K', \end{matrix}

amiből következik,

C_{2} E ∥ O' K' ∥ O_{3} K_{3}

lévén, hogy

\begin{matrix} E O_{3} = E O' . \end{matrix}

(4)

O'

-ból vonjuk

O' H ∥ A B

, amely egyenes

E F

-et

G

-ben találja. Minthogy

G O' E Δ \sim H O' O_{3} Δ

, a

(4)

-re való tekintettel

\begin{matrix} G E : H O_{3} = 1 : 2. \end{matrix}

(5)

De a rajzból láthatólag:

\begin{matrix} G E = G C_{2} + C_{2} E = r + C_{2} E, \end{matrix}

\begin{matrix} H O_{3} = H K_{3} + K_{3} O_{3} = r + r_{3}, \end{matrix}

amely értékeket

(5)

-be helyettesítve és

C_{2} E

-t meghatározva, ered:

\begin{matrix} C_{2} E = \frac{1}{2} (r_{3} - r) . \end{matrix}

(6)

Ezt az egyenlőséget

(3)

-mal egybevetve kapjuk:

\begin{matrix} x_{3} = R - \frac{1}{2} (r_{3} - r) . \end{matrix}

(7')

Az utolsó kifejezést még átalakítjuk, annak tekintetbe vételével, hogy

\begin{matrix} r_{1} + r_{2} + r_{3} - r = 4 R \end{matrix}

(8)

Innen ugyanis

\begin{matrix} R = \frac{1}{4} r_{1} + r_{2} + r_{3} - r), \end{matrix}

amit

(7')

-be téve, lesz:

\begin{matrix} x_{3} = \frac{1}{4} (- r_{1} + r_{2} + r_{3} + r) . \end{matrix}

(7)

Egészen hasonló két kifejezést kaphatunk

x_{1}

és

x_{2}

-re.
Következmény. A

(2)

egyenletek alapján még ezeket nyerjük:

\begin{matrix} m_{1}' = \frac{1}{2} (- r_{1} + r_{2} + r_{3} + r), \end{matrix}

\begin{matrix} m_{2}' = \frac{1}{2} (r_{1} - r_{2} + r_{3} + r), \end{matrix}

(9)

\begin{matrix} m_{3}' = \frac{1}{2} (r_{1} + r_{2} - r_{3} + r) . \end{matrix}

Megjegyzés.

1.

(8)

egyenlőséget újólag bebizonyíthatjuk, csak

C_{2} F

-et kell kifejeznünk. A megelőzőhöz egészen hasonló meggondolásokból következik, hogy

\begin{matrix} C_{2} F = \frac{1}{2} (r_{1} + r_{2}) . \end{matrix}

(10)

Minthogy pedig

\begin{matrix} C_{2} F + C_{2} E = 2 R, \end{matrix}

(6)

és

(10)

egyenletek összeadása a

(8)

összefüggést igazolja.

2.

(9)

kifejezések tompaszögű háromszögnél annyiban változnak, hogy a tompaszög csúcsán átmenő magasság-darabot negatív jellel kell venni.

3.

A háromszög csúcsaiból a rajtuk át nem menő két magassági vonalhoz vont párhuzamosak a körülírt körbe írt hatszöget határolnák, melynek területe egyenlő a háromszög területének kétszeresével.
A hatszög legyen

A 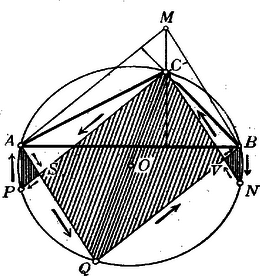Q B N C P

, ahol

\begin{matrix} A Q ∥ B M ∥ C N \end{matrix}

stb. és azonkívül:

\begin{matrix} A Q = C N = m'_{2}, A P = B N = m'_{3}, B Q = C P = m'_{1} . \end{matrix}

(a)

Hegyesszögű háromszögnél az

(1)

pontban mondottak a bizonyítást megadják, ha megjegyezzük, hogy pl.

B N C Δ ≅ C M B Δ

(

1

. rajz).

(b)

Tompaszögű háromszög esetében a hatszög kerülete önmagát metszi. Ezért ezt az esetet részletesebben kell tárgyalnunk. Mindenekelőtt értelmeznünk kell ilyen esetre a területet. Ennek módjáról már e lapokban volt szó.^{$^{*}$}
Ebben az esetben a kerület önmagát az

S

és

V

pontokban metszi (

3

. rajz). A hatszög területe most a

C S Q V

parallelogrammából és az

A P S, B V N

háromszögekből áll. Ha a kerületet az

A Q B N C P A

rendben végig járjuk, a parallelogramma kerülete pozitív, a két háromszögé negatív körüljárású lesz, ezért a területet

(T)

az idézett helyen mondottak szerint így kell értelmeznünk:

\begin{matrix} \bar{T} = C S Q V - A P S - B V N . \end{matrix}

Az oldalok párhuzamos volta miatt, és mert

A P = B N

\begin{matrix} A P S Δ ≅ B V N Δ, \end{matrix}

tehát

\begin{matrix} \bar{T} = C S Q V - 2 A P S . \end{matrix}

(11)

Másfelől vegyük tekintetbe, hogy a háromszög

T

területe igy fejezhető ki:

\begin{matrix} T = A B C = A B M - C B M - A C M . \end{matrix}

vagy egybevágó háromszögekkel helyettesítve:

\begin{matrix} T = A Q B - A P C - B C N . \end{matrix}

Eszerint írhatjuk:

\begin{matrix} 2 T = A B C + A Q B - A P C - B C N . \end{matrix}

(12)

Azonban (a

3

. rajzon láthatólag):

\begin{matrix} A B C + A Q C = C S Q V + A S C + B C V, \end{matrix}

\begin{matrix} A P C = A P S + A S C, \end{matrix}

\begin{matrix} B C N = B V N + B C V, \end{matrix}

úgy hogy

(12)

-be helyettesítve ezt kapjuk:

\begin{matrix} 2 T = C S Q V - A P S - B V N . \end{matrix}

(13)

(11)

és

(13)

egybevetéséből ered végül

\begin{matrix} \bar{T} = 2 T . \end{matrix}

(14)

A hatszög minden esetben szimmetrikus,

3

pár csúcsának összekötő egyenesei

(A N, B P, C Q)

átmérők, s mindenik felezi az idomot.
Tompaszögű háromszög esetében csak a tompaszög csúcsából kiinduló átmérő (itt :

C Q

) halad a hatszög belsején át.

C Q

egyszersmind átlója a

C S Q V

parallelogrammának.

4.

A megelőző pontban mondottakból következik, hogy
Mindig találhatunk olyan átmérőt, mely a hatszöget két egyenlő területű húrnégyszögre osztja. Ha

C ∢

a háromszög legnagyobb szögét jelöli, akkor mindenesetre:

\begin{matrix} A Q C P A = T . \end{matrix}

(15)

Evvel az elül jelzett tételnek első felét bebizonyítottuk.

5.

A tétel második felének bebizonyítására térünk át. Legyen először

A B C

hegyesszögű háromszög. Meghatározzuk az

A Q C P A

négyszög területét az oldalaiból.
Legyen

\begin{matrix} Q C = a', C P = b', P A = d', A Q = c', \end{matrix}

akkor (lásd

1

. pont)

\begin{matrix} a' = 2 R, b' = m'_{1}, c' = m'_{3}, d' = m'_{2} . \end{matrix}

Vegyük tekintetbe a

(8)

és

(9)

összefüggéseket, akkor lesz:

\begin{matrix} s' = \frac{1}{2} (a' + b' + c' + d') = \frac{1}{4} (r_{1} + r_{2} + r_{3} + 4 R) \end{matrix}

\begin{matrix} = \frac{1}{4} (r_{1} + r_{2} + r_{3} - r + 4 R + 4 r), \end{matrix}

vagy

\begin{matrix} s' = 2 R + r, \end{matrix}

(16)

továbbá

\begin{matrix} s' - a' = r, \end{matrix}

\begin{matrix} s' - b' = 2 R + r - \frac{1}{2} (- r_{1} + r_{2} + r_{3} + r) \end{matrix}

\begin{matrix} = 2 R + \frac{1}{2} (r + r_{1} - r_{2} - r_{3}) . \end{matrix}

2 R

-et

(8)

-ból kifejezve, összevonás után

\begin{matrix} s' - b' = r_{1}, \end{matrix}

és hasonlóan:

\begin{matrix} s' - c' = r_{2}, \end{matrix}

(16')

\begin{matrix} s' - d' = r_{3} . \end{matrix}

Innen, a húrnégyszög területének ismert képletébe:

\begin{matrix} A Q C P A = \sqrt[]{(s' - a') (s' - b') (s' - c') (s' - d')} \end{matrix}

helyettesítve, (15)-re való tekintettel, ered:

\begin{matrix} T = \sqrt[]{r r_{1} r_{2} r_{3}} . \end{matrix}

(17)

Tompaszögű háromszög esetében a négyszög területének képlete annyiban módosul, hogy

c'

-t mindenütt negatív jellel kell venni.^{$^{*}$}
A számítás maga, s így a

(17)

végső képlet nem szenved változást.
A

3 - 5

. pontokban a

(17)

képletnek geometriai levezetése foglaltatik.

^*RátzL.Math.Gyakorlókönyv11.k.67.l.502.feladat.

^*RátzL.Math.GyakorlókönyvII.k.67.l.498.feladat.

^*L.Math.GyakorlókönyvII.68.l.508.feladat.

^{$^{*}$}Lásd $≪$ Megjegyzések a talpponti háromszögről $≫$ c. közleményben K.M.L. IX. évf. 126. lapon; v.ö. Baltzer: Elemente der Mathematik III. k. 6. kiadás, 67‐69. lap.

^{$^{*}$}L. K.M.L. XII. évf. 78. lapon.