Kezdőlap


Cím:	A Poinsot-féle polyéderekről 2.
Szerző(k):	Dr. Bozóky Endre
Füzet:	1905/január, 113 - 119. oldal	PDF \| MathML
Témakör(ök):	Szakmai cikkek

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

$7$ . A polyederek fajtájának megállapítása. Hogy Euler tétele ezen új polyederekre is alkalmazható legyen, annak módosításánál tekintettel kell lennünk az illető polyeder fajtájára, lapjainak fajtájára és testszögleteinek fajtájára. Az oldallapok, illetőleg a testszögletek egymást közt külön-külön egyenlő fajtájúak.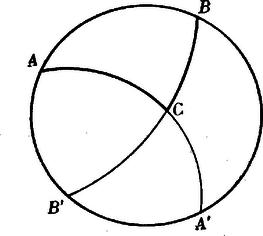
E célból vetítsük a polyedert a körülírt vagy beírt gömbre, vetítési középpontul ezen gömbök közös középpontját használván fel.
A következő jelöléseket fogjuk alkalmazni:
$n$ a polyeder oldallapjának oldalszáma (rendje),
$φ$ az a szám, mely az oldallap faJtáját jelzi,
$a$ az a sphaerikus terület, melyet az oldallap vetülete beborít,
$s$ ezen sphaerikus sokszögnek belszögösszege.
Bontsuk fel ezt a sphaerikus sokszöget a $3$ . pontban jelzett módon gömbháromszögekre. Egy ilyen gömbháromszög belszögösszege legyen $α$ .
Ha szögegységül a derékszöget, területegységül azt a gömbháromszöget vesszük, melynek mindhárom szöge derékszög, akkor gömbháromszögünk területe $= a - 2$ .

Ugyanis egészítsük ki az

A B

legnagyobb gömbi körívet körré és hosszabbítsuk meg az

A C, B C

köríveket az ezen körrel való

A'

és

B'

metszéspontjaikig.

\begin{matrix} A B C + B C A' = (A) \end{matrix}

\begin{matrix} A B C + A C B' = (B) \end{matrix}

\begin{matrix} A B C + B' C A' = (C), \end{matrix}

hol

(A), (B), (C)

A B C

szögekhez tartozó gömbi kétszögeket jelentik.
Egyenleteinket összeadván, a bal oldalon a félgömböt és az

A B C

háromszög területének kétszeresét kapjuk; választott egységeinkre való tekintettel pedig a gömbkétszög területe egyenlő a hozzátartozó szög kétszeresével; ha tehát

S

a gömbháromszög területe, akkor

\begin{matrix} 2 S + 4 = 2 A + 2 B + 2 C, \end{matrix}

honnét

\begin{matrix} S = A + B + C - 2, \end{matrix}

\begin{matrix} S = a - 2. \end{matrix}

Ezen kitérés után visszatérvén eredeti feladatunkhoz, látnivaló, hogy az oldallap vetületének a területe ezen gömbháromszög

n

-szerese lévén

\begin{matrix} a = Σ a - 2 n . \end{matrix}

Itt

Σ a

a tekintetbe vett

n

gömbháromszög belszögeinek összege, más szóval a gömbi polygon belszögeinek összege

s

, melyhez még hozzáadandó a háromszögek közös csúcspontja körül fekvő szögek összege.
Ez az utóbbi

= 4 φ

, ha

φ

alatt a vetített oldallap fajtáját értjük.
Ennélfogva

\begin{matrix} a = s + 4 φ - 2 n . \end{matrix}

(1)

Legyen

E

a polyeder fajtáját, jellemző szám. Értelmezésünk szerint ez a szám azt jelzi, hányszorosan borítják a polyeder oldallapjainak vetületei a gömb felületét. Ha

l

az oldallapok száma, akkor, minthogy választott egységünknek megfelelőleg a gömb felszíne

= 8

, tehát

\begin{matrix} l a = 8 E . \end{matrix}

(2)

e

a polyeder éleinek száma, akkor

\begin{matrix} l n = 2 e . \end{matrix}

(3)

Jelöléseink szerint

s

alatt a sphaerikus sokszögek belszögeinek összegét értjük, tehát

l s

az összes oldallapok vetületeit alkotó sphaerikus sokszögek belszögeinek totalitásával egyenlő. Ha

σ

alatt a polyeder egy testszögletének fajtáját osztják, akkor az egy pont körül fekvő szögek összege (minthogy egy csúcspont körül a testszöglet összes lapjainak vetületei fekszenek)

σ

-szorosa a teljes szögnek, s így

c

számú csúcspont esetében

\begin{matrix} l s = 4 σ c . \end{matrix}

(4)

(1)

egyenlet

l

-szeresét összehasonlítván a

(2)

egyenlettel,

\begin{matrix} 8 E = l s + 4 l φ - 2 n l \end{matrix}

származik, honnét

\begin{matrix} l s = 8 E - 4 l φ + 2 n l . \end{matrix}

Ezt a

(4)

egyenlettel vetvén egybe:

\begin{matrix} 8 E - 4 l φ + 2 n l = 4 σ c \end{matrix}

De a

(3)

egyenlet tekintetbe vételével:

\begin{matrix} 8 E - 4 l φ + 4 e = 4 σ c \end{matrix}

s ezt

(4)

-gyel egyszerűsítvén, a tagok kellő áthelyezésével

\begin{matrix} e + 2 E = φ l + σ c . \end{matrix}

(5)

származik, mely egyenlet az Euler-félének általánosítása.
Ugyanis convex polyederek esetében

\begin{matrix} E = φ = σ = 1 \end{matrix}

s ha ezekét helyettesítjük, akkor

(5)

-ből

\begin{matrix} e + 2 = l + c, \end{matrix}

vagyis Euler egyenlete származik.
Ezek után nem marad egyéb hátra, mint egyenletünket a polyederekre rendre alkalmazván, ezen testekkel közelebbről megismerkedni.

8

. Heted-fajtájú szabályos dodekaeder. Ezt a testet csillagos, vagyis másodfajú ötszöglapok határolják, melyek a convex dodekaeder minden csúcsában elsőfajú háromélű testszögleteket alkotnak.
Minthogy a convex dodekaedernek

20

csúcspontja van, ennélfogva ennek az új testnek is

20

csúcspontjának kell lennie.
Ha

m

alatt a testszögletek éleinek számát,

n

alatt az oldallapok oldalainak számát értjük, akkor

\begin{matrix} 2 e = m c és 2 e = n l . \end{matrix}

Esetünkben:

\begin{matrix} c = 20, m = 3, n = 5, \end{matrix}

tehát

\begin{matrix} e = 30 és l = 12. \end{matrix}

(5)

számú alapegyenletünkbe ezen értékeken kívül

σ = 1

és

φ = 2

tétetvén

\begin{matrix} 2 E = 24 + 20 - 30 = 14 \end{matrix}

származik, s így ez a dodekaeder tényleg

7

-ed fajú.

9

. Hetedfajtájú szabályos ikosaeder. Ezt a testet szabályos háromszögek határolják, melyek a convex ikosaeder minden csúcspontjában másodfajú ötélű testszögleteket alkotnak. Ennélfogva az új testnek

12

csúcspontja van.
Ha tehát

\begin{matrix} c = 12, m = 5 és n = 3, \end{matrix}

akkor

\begin{matrix} e = 30 és l = 20. \end{matrix}

Az alapegyenletbe ezeken kívül

σ = 2

és

φ = 1

helyettesíttetvén,

\begin{matrix} 2 E = 20 + 24 - 30 = 14 \end{matrix}

származik, s így ez az ikosaeder tényleg

7

-ed fajú.

10

. Harmadfajú szabályos dodekaeder convex oldallapokkal. Ezt a testet convex szabályos ötszögek határolják, melyek egy közönséges szabályos ikosaeder minden csúcspontjában másodfajú ötélű testszögleteket alkotnak. A testnek

12

csúcspontja levén,

\begin{matrix} m = 5 és n = 5, \end{matrix}

helyettesítése alapján

\begin{matrix} e = 30 és l = 12. \end{matrix}

Az alapegyenletbe ezeken kívül

σ = 2, φ = 1

tétetvén

\begin{matrix} 2 E = 12 + 24 - 30 = 6, \end{matrix}

s így ez a dodekaeder tényleg harmadfajú.

11

. Harmadfajú szabályos dodekaeder csillagos oldallapokkal. Ezt a testet csillagos szabályos ötszögek határolják, melyek egy közönséges szabályos ikosaeder minden csúcspontjában elsőfajú ötélű testszögletet alkotnak. A testnek

12

csúcspontja levén,

m = 5

és

n = 5

helyettesítése alapján

e = 30

és

l = 12

Az alapegyenletbe ezeken kívül

σ = 1, φ = 2

tétetvén

\begin{matrix} 2 E = 24 + 12 - 30 = 6, \end{matrix}

s így ez a csillagos ötszöglapú dodekaeder tényleg harmadfajú.

12

. Az új polyederek meghatározó elemeit, melyeket a megelőzőkben rendre kiszámítottunk, az alábbi táblázatban foglaljuk össze.

\begin{matrix} \begin{matrix} l \end{matrix} \end{matrix}

Ebből a táblázatból kitűnik, hogy az új polyederek páronkint conjugáltak, éppen úgy, mint a convex polyederek.

13

. A polyederek előállításának módja Cauchy szerint. Eddigi tárgyalásaink alapján az új polyederekről némi fogalmat alkothatunk magunknak, melyet vázlatos rajzaink bizonyos mértékben támogathatnak. De ezek az új testek bizonyára oly bonyolódott alakzatok, melyekről csak tökéletes modellek szemlélete nyújthatna tiszta képet. Nem lesz tehát fölösleges, ha a róluk alkotott eddigi képet azzal egészítjük ki, hogy ismertetjük Cauchy-nak már a

3

. pontban jelzett szerkesztési módját.
Cauchy szerint ugyanis ezeket a polyedereket a következő módon nyerhetjük:
"Ha a közönséges dodekaeder éleit, melyek a

12

ötszögnek oldalait alkotják, meghosszabbítjuk, akkor a harmadfajú csillagos lapú dodekaedert kapjuk."
"Ha a közönséges dodekaeder minden oldallapját addig terjesztjük ki, míg az a szemköztes oldallapot határoló öt lapot metszi, akkor a harmadfajú convex oldallapú dodekaedert kapjuk."
"Ha ebben az utóbbi dodekaederben azokat az éleket hosszabbítjuk meg, melyek a

12

convex ötszögnek oldalai, akkor a hetedfajú dodekaederhez jutunk."
"A hetedfajú ikosaedert úgy szerkeszthetjük meg, ha a közönséges ikosaedernek oldallapjait addig terjesztjük ki, míg a szemköztes oldallapot körülvevő három háromszöglapot metszi."
A megelőzőkben előadottakra nézve Rouché et Comberousse Traité de Géometrie (II. k. p. 247-2571) című kitűnő művet vettem alapul, s a kérdések iránt érdeklődőket is erre a munkára figyelmeztetem.