Cím: A Poinsot-féle polyéderekről 1.
Szerző(k):  Dr. Bozóky Endre 
Füzet: 1904/december, 65 - 71. oldal  PDF  |  MathML 
Témakör(ök): Szakmai cikkek

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A K. M. L. X. évfolyamának 4., 5. és 6. számában a polyederekről írt cikkemben arra törekedtem, hogy a lap t. olvasóinak a polyederekre vonatkozó, s az iskolában szerzett ismereteit a tanterv szűk határain túl kiterjesszem. Ezt a célt tűzöm magam elé most is, amidőn az ott tárgyaltakat a Poinsot-féle polyederek ismertetésével szándékozom kiegészíteni.
1. Az m oldalú szabályos sokszögek száma. Tegyük föl, hogy a kör kerületét m számú egyenlő részre osztottuk fel, és legyen a a körkerület egy ilyen részének hosszúsága. Ha az osztáspontokat p-enkint összekötjük, akkor egy a körbe írt polygont kapunk. Itt két eshetőséggel kell számolnunk, aszerint, amint m és p viszonylagos törzsszámok, illetőleg van legnagyobb közös mértékük ϑ.
Ha m és p viszonylagos törzsszámok, akkor a kör kerületét p-szer járván körül, eredeti kiinduláspontunkhoz kell visszakerülnünk; mert a húrhoz tartozó körív hosszúsága pa, az egész körnek kerülete ma, s ennek a két mennyiségnek pma a legkisebb közös többszöröse.
Ha m és p oly számok, melyeknek ϑ a legnagyobb közös mértékük, akkor a húrhoz tartozó körív pa hosszúsága és az egész kör ma kerülete oly két szám, amelynek mpϑa a legkisebb közös többszöröse, s ez esetben a kör kerületét pϑ-szer körüljárván, eredeti kiinduláspontunkhoz kell visszajutnunk.
Az első esetben a húrhoz tartozó pa ívet m-szer raktuk fel a körre, s így m-oldalú polygont nyertünk; a második esetben a pa ívet mϑ-szor raktuk fel a körre, tehát a nyert polygon oldalszáma mϑ lesz.
Minthogy ez utóbbi esetben m-nél kevesebb oldalszámú polygont nyerünk, ennélfogva, ha azt kérdezzük, hogy hány m-oldalú szabályos polygon létezik ezt az esetet mellőzhetjük.
Az eddigiek szerint kérdésünkre azt a feleletet kapjuk, hogy annyi m-oldalú polygon létezik, ahány az m-hez viszonylagos törzsszám található az

1,2,...,m-1
számsorban. Minthogy azonban ugyanazt a polygont kapjuk, akár p-enkint, akár pedig (m-p)-enkint kötjük össze az osztáspontokat,- ennélfogva annyi m-oldalú szabályos polyqon létezik, ahány az m-hez viszonylagos törzsszám található az
1,2,...,m-12
számsorban. Eszerint van:
2szabályos ötszög,
1"hatszög,
3"hétszög stb.
Az így származó szabályos sokszögek közül az egyik convex polygon, a többiek pedig csillagos polygonok.
Poinsot (Journal de l'École Polytechnique, t. IV, p. 25.) a kérdés algebrai alapon való tárgyalására nézve azt jegyzi meg, hogy a szabályos polygon oldalának hosszúságát oly magasabb fokú egyenlet szolgáltatja, melynek összes gyökei valósak, amely tehát egyszerre az összes lehetséges m-oldalú szabályos polygonok oldalait szolgáltatja.
Az m oldalú szabályos polygont m-edrendűnek fogjuk nevezni; fajtája azon p számtól függ, amely a polygon keletkezésénél szerepet játszik. Minthogy az m-oldalú, p-fajtájú szabályos polygon esetében a kör kerületét p-szer járjuk körül, ennélfogva az oldalaihoz mint húrokhoz tartozó középponti szögek összege 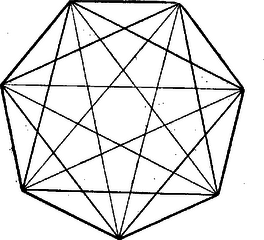=p⋅4R.
 
 

Az 1. ábra a lehetséges 7-edrendű polygonokat tünteti fel, melyek közül az 1-ső fajtájú konvex, a 2-od és 3-ad fajtájúak pedig csillagosak. Az ábrából kitűnik, hogy a 2-od fajtájú mint magot magában foglalja az 1-ső fajtájút; a 3-ad fajtájú megrajzolásánál pedig mind a 2-od, mind az 1-ső fajú polygonok újra fellépnek.
Viszont, ha a convex polygonból indulunk ki, akkor az oldalak meghosszabbításával az összes magasabb fajtájú polygonokig eljuthatunk.
2. Magasabb fajtájú testszögletek. Tekintsünk egy olyan egyenes gúlát, melynek alapja szabályos 7-edrendű sokszög. A gúla csúcsánál keletkező testszöglet ugyancsak 7-edrendű, mert éleinek és oldalainak száma egyaránt 7; de a fajtája az alapsokszögnek vagy bármely egyéb síkmetszetének fajtájától függ. Ha a gúla oldallapjait az alapra vetítjük, akkor ezek a vetületek az 1-ső fajtájú alap esetében az alapot 1-szer, a 2-od fajtájú alap esetében 2-szer, a 3-ad fajtájú esetében pedig 3-szor borítják be. Így tehát a testszögletek is két számmal jellemezhetők, melyek közül az egyik a testszögletnek rendjét, a másik pedig a fajtáját állapítja meg. 3. Magasabb fajtájú szabályos polyederek. Poinsot a fentebb idézett helyen következő módon okoskodik:
"Megtartván a szabályos polyederek általános értelmezését, beláthatjuk annak a lehetőségét, hogy nemcsak az új szabályos polygonok segítségével, hanem a régiekkel is újfajta szabályos polyedereket szerkeszthetünk; hogy ezt a dolgot jól megértsük, pontosan meg kell állapodnunk az iránt, mit értsünk a polyeder oldallapja, éle és csúcsa alatt.
A polyeder oldallapjaiul azokat a szabályos sokszögalakú síklapokat tekintjük, melyeknek minimális száma elegendő a polyeder teljes körülhatárolásához.
Az élek egyúttal az oldallapok határvonalai; továbbá az élek oly egyenesek, melyek mentén a szomszédos oldallapok összefüggenek. Eszerint minden él két szomszédos laphoz tartozik, s így az élek száma mindig félakkora, mint a lapok oldalainak összesége.
Egyedül az élek mentén keletkeznek a polyedernek lapszögei; azok a többi lapszögek, melyeket az egymáson keresztülhatoló lapok egyebütt alkothatnak, ezek közé nem számíttatnak; hasonlóképpen egyedül az élek végpontjaiban keresendők a polyeder csúcsai, a polyederen található testszögleteknek csúcspontjai.
Ezekre való tekintettel világos, hogy tökéletesen szabályos új polyedereket szerkeszthetünk, melyeknek oldallapjai egybevágó szabályos sokszögek, melyek egymással kettenkint mindenütt egyenlő hajlásszöget alkotnak, s amelyek minden csúcs körül egyenlő számban találkoznak.
A polyedereknek meg van a körülírt és beírt gömbjük is.
Ezek a polyederek a közönséges szabályos polyederektől lényegesen csupán abban különböznek, hogy az utóbbiak oldallapjait a beírt vagy körülírt gömbre vetítvén, a vetületeikül tekintendö gömbi sokszögek csak egyszer borítják be a gömb felületét; ellenben az előbbieknél az oldallapok vetületei a gömb felületét többszörösen borítják be."
Az utóbbinak felvilágosítása céljából tekintsük a polyeder egy oldallapját, mely lehet convex sokszög, de lehet csillagos sokszög is. Legyenek a1a2...an a lap csúcspontjainak, ω pedig a lap középpontjának a gömbfelületen fekvő vetületei. A vetítés a gömb sugarainak segítségével történvén, ha a körülírt gömböt tekintjük, akkor csupán az ω pont keresendő fel; ha a beírt gömbre vetítünk, akkor csupán az ω pontot nem kell külön megszerkeszteni, lévén az a gömbnek a lappal való érintkezési pontja. Ha már most arról van szó, mennyiben borítja a lap vetülete a gömbfelületet, akkor ez alatt az
ωa1a2,ωa2a3,...,ωana1
gömbháromszögek területeinek összegét fogjuk érteni.
Ennek alapján, hasonlóképpen, mint a polygonok esetében, megkülönböztetjük a polyeder rendjét és fajtáját. A polyeder rendje alatt oldallapjainak számát, fajtája alatt pedig azt a számot értjük, mely mutatja, hogy a polyeder oldallapjainak vetületei hányszorosan borítják a polyederrel kapcsolatos gömb felületét.
Az 1. pont végén megjegyeztük, hogy a polygon oldalainak meghosszabbításával az összes magasabb fajtájú polygonokhoz eljuthatunk, s a kiindulásul szolgáló polygon mintegy a szerkesztés magjaként szerepel. Erre az alapgondolatra támaszkodva Cauchy a Journal de l'École Polytechnique IX. kötetében (p. 68) megszerkesztette a Poinsot-féle polyedereket, amennyiben egy szabályos convex polyedert választván a szerkesztés magjául, az oldallapok kiterjesztésével, illetőleg az élek meghosszabbításával az új polyederhez jutott.
Nem sokkal később Bertrand a Comptes rendus de l'Akadémie des Sciences XLVI. kötetében az új polyedereket ugyancsak szoros kapcsolatba hozta a régiekkel, s minthogy tárgyalásának gondolatmenete a Cauchy-énál egyszerűbb, azért az alábbiakban ezt fogjuk ismertetni.
4. Alaptételek. A tárgyalás első sorban a következő alaptételre támaszkodik: ha a térben fekvő tetszésszerinti számú pontot tekintünk, akkor mindig találunk oly convex polyedert, melynek csúcspontjai az adott pontokkal egybeesnek, s mely a többi pontokat magában foglalja.
Természetes dolog, hogy a tétel akkor is áll, ha a térbeli pontok mindannyian rendre egybeesnek a polyeder csúcspontjaival. Ebben az esetben az adott pontok közül egyetlenegy sem fekszik a polyeder belsejében. Továbbá a polyederekről szóló korábbi cikkünkben (K. M. L. X. évf. p. 91.) bebizonyítottuk azt, hogy nincs olyan convex polyeder, amelynek csúcsaiban 5-nél több oldallap (él) találkoznék.
5. Minden tetszésszerinti fajtjú A szabályos polyederhez találhatni oly X szabályos convex polyedert, melynek csúcsai az adott polyeder csúcsaival egybeesnek.
Az adott A polyedernek csúcsai egy bizonyos gömbfelületen, a körülírt gömbön fekszenek; ha tehát egy olyan convex polyedert tekintünk, melynek csúcsai A-nak csúcsaival összeesnek, akkor az A-nak többi csúcsait nem zárhatja magába.
Alaptétetünkre való tekintettel kell tehát egy olyan X convex polyedernek léteznie, melynek összes csúcspontjai az A polyeder csúcspontjaival egybeesnek.
Bebizonyítandó, hogy az az X convex polyeder szabályos.
Az A és X polyederek együttvéve egy P térbeli idomot alkotnak. Tekintsünk egy ezzel egybevágó Q térbeli idomot.
Minthogy az A polyeder szabályos, ennélfogva a P és Q idomok oly föltétel mellett is födéshez hozhatók, hogy Q-nak bármely csúcspontja P-nek egy meghatározott csúcspontjával essék össze.
Ebből következik, hogy az X convex polyeder összes testszögletei egybevágók.
Ha az idomoknak két csúcsa már egybeesik, akkor a P és Q idomok részét tevő A polyederek coincidentiája, s így a teljes idomok egybeesése is még legalább három különböző módon érhető el. Az egybeeső két csúcs ‐ minthogy a testek csúcsaiban három, négy vagy öt oldallap találkozhat‐ legalább is egy háromélű testszöglethez tartozik; az első idom triederének egyik lapjára a másik idom triederének bármelyik lapja helyezhető, s így ha háromélű testszögletek állanak rendelkezésre, a coincidentia háromféleképpen, négyélűeknél négyféleképpen, ötélűeknél ötféleképpen létesíthető.
Ennélfogva a két alakzat X polyedereinek testszögletei nemcsak egyenlőek, de legalább is háromféle módon hozhatók coiucidentiába, s így ezen testszögletek lapjai egyenlőek és egymással egyenlő hajlásszögeket zárnak be.
Innét következik, hogy az X polyeder oldallapjai egyfajtájú és egyenlőszögű (három-, négy- vagy ötszögek) sokszögek, s hogy az oldallapok egymáshoz egyenlő szögek alatt hajlanak.
Abból, hogy a két alakzat coincidentiája azon föltétel mellett is elérhető, mely szerint Q-nak egy tetszésszerinti csúcsa P-nek egy meghatározott csúcsára helyeztetik, az következik, hogy az X polyeder oldallapjai szabályos polygonok.
Mindezeket egybefogialva, világos, hogy az X polyeder szabályos test.
6. Csakis négyféle magasabb fajú polyeder létezik. A megelőző tétel alapján Bertrand a magasabb fajú szabályos testek előállítására a következő módot állapítja meg.
Induljunk ki valamely szabályos convex polyederből; válaszunk ezen egy csúcspontot és keressünk rajta oly csúcspontokat, melyek a kiválasztottal egyetemben szabályos polygont szolgáltatnak.
Az így nyert polygon oldallapja lehet annak a magasabb fajtájú polyedernek, melynek összes csúcspontjai a kiindulásul választott convex polyeder összes csúcspontjaival egybeesnek.
Ha ezen eljárás mellett tényleg eljutunk egy magasabb fajtájú polyederhez, akkor az egy csúcspontban találkozó polygonok száma az illető polyeder testszögleteinek lapszámát szolgáltatja. Hogy tényleg testet kaphassunk, ahhoz szükséges, hogy a polygonok testszögletet alkothassanak.
Közvetlenül világos hogy ezt a constructiót a tetraéderre nem alkalmazhatjuk.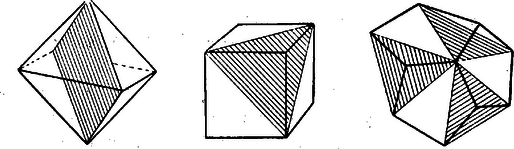
 
 

Az oktaédernek minden csúcspontja két négyzethez tartozik, s ezek ‐ nem feküdvén ugyanabban a síkban ‐ nem alkothatnak együttesen polygonális lapot.
A hexaedernek minden csúcspontja más kettővel egyenlőoldalú háromszöget alkot, még pedig háromféleképpen; de ez a három szabályos háromszög egyazon szabályos tetraederhez tartozik.
A dodekaedernek minden csúcspontja háromféleképpen alkothat két további csúcsponttal szabályos háromszögeket; de ez a három lap nem alkothat triédert, mert kettő-kettőnek nincsen közös élük.
A dodekaedernek minden csúcspontja a benne találkozó lapokkal szomszédos lapokról vett két‐ két csúcsponttal hat egyenlőoldalú háromszöget alkot; de ezek a lapok két szabályos tetraedernek oldallapjai.
Végre a dodekaedernek minden csúcspontja közös csúcspontja lehet három szabályos ötszögnek, melyeknek többi négy csúcsai egyugyanazon triederhez tartoznak. Ha ezek az ötszögek convexek, akkor, nem lévén közös élük, nem alkothatnak triedert; de ha csillagosak, akkor triedert alkotván, összeségük határolja a 7-ed fajtájú dodekaedert.
Az ikosaedernek minden csúcspontja öt szabályos háromszögnek közös csúcspontja. Ezen háromszögek oldalai azok a legrövidebb egyenesek, melyeket a csúcspontok közt húzhatunk, de amelyek a testnek nem élei. Ezek a háromszögek zárják be a 7-ed fajtájú ikosaedert.
Az ikosaedernek minden csúcspontja öt convex szabályos ötszögnek lehet közös csúcspontja; ezen ötszögek többi négy csúcspontja szintén az ikosaederhez tartozik. Ezek az ötszögek a 3-ad fajtájú, convex oldallapú dodekaedert határolják.
Végre ugyanezek a csúcspontok csillagos ötszögeket is adnak, melyek a 3-ad fajtájú, csillagos oldallapú dodekaedert határolják. Ezeken kívül több új polyeder nem keletkezhetik.