Kezdőlap


Cím:	Goniometriai és trigonometriai alaptételek
Szerző(k):	Antal Márkus
Füzet:	1905/március, 153 - 157. oldal	PDF \| MathML
Témakör(ök):	Szakmai cikkek

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Első segédtétel. Egyenlő kerületi hegyesszögekhez tartozó húrok viszonyai saját körük átmérőihez egyenlők.
Bizonyítás. Jelöljük a $2 r_{1}$ illetőleg $2 r_{2}$ átmérőjű körökben az $α$ kerületi szöghöz tartozó húrok hosszait $a_{1}$ -gyel és $a_{2}$ -vel és válasszuk ki éppen azokat a kerületi szögeket, melyeknek egyik száruk átmegy a körök $O_{1}$ , illetőleg $O_{2}$ középpontján. Ez esetben két hasonló derékszögű háromszöget nyertünk, melyekből:

\begin{matrix} \frac{a_{1}}{2 r_{1}} = \frac{a_{2}}{2 r_{2}} . \end{matrix}

Második segédtétel. Ha két kerületi hegyesszöghöz tartozó húrok viszonyai saját körük átmérőihez egyenlők, akkor a két kerületi szög is egyenlő.
Bizonyítás. A

2 r_{1}

és

2 r_{2}

átmérőjű körökben az

a_{1}

, illetőleg

a_{2}

húrokon nyugvó kerületi hegyesszögek közül válasszuk ki éppen azokat, melyeknek egyik száruk átmegy a körök középpontjain. Minthogy az így keletkező két derékszögű háromszögben

\begin{matrix} \frac{a_{1}}{2 r_{1}} = \frac{a_{2}}{2 r_{2}}, \end{matrix}

azért a háromszögek hasonlók és így az

a_{1}

és

a_{2}

húrokkal szemben fekvő kerületi hegyesszögek is egyenlők.
Nevezzük az

α

kerületi hegyesszöggel szemben fekvő

(a)

húr viszonyát az átmérőhöz

(2 r)

α

szög sinusának

\begin{matrix} sin α = \frac{a}{2 r}, \end{matrix}

akkor az

(1)

és

(2)

segédtétel így foglalható össze:
Valamely hegyesszög egyértelműleg határozza meg sinusát és valamely hegyesszög sinusa egyértelműleg határozza meg magát a szöget. Minthogy a húr mindig kisebb az átmérőnél, azért valamely hegyes szög sinusa mindig pozitív valódi tört.
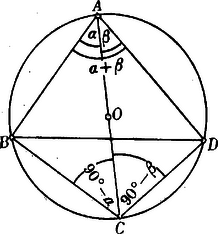
I. alaptétel. Ha az

α

és

β

hegyesszögek összege ismét hegyesszög, akkor

\begin{matrix} sin (α + β) = sin α \cdot sin (90^{\circ} - β) + sin (90^{\circ} - α) sin β . \end{matrix}

Bizonyítás. Mérjük az

α

és

β

szögeket az

A C

átmérő két különböző oldalára, úgy hogy

C A B ∢ = α

és

C A D ∢ = β

legyen, akkor Ptolemaios tétele értelmében

\begin{matrix} B D \cdot A C = A D \cdot B C + A B \cdot C D . \end{matrix}

Minden tagot

{\bar{A C}}^{2}

-tel osztva

\begin{matrix} \frac{B D}{A C} = \frac{A D}{A C} \cdot \frac{B C}{A C} + \frac{A B}{A C} \cdot \frac{C D}{A C} \end{matrix}

vagyis:

\begin{matrix} sin (α + β) = sin α \cdot sin (90^{\circ} - β) + sin (90^{\circ} - α) sin β . \end{matrix}

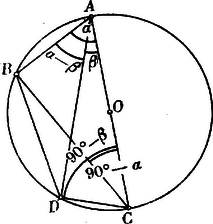
II. alaptétel. Ha az

α

és

β

hegyesszögek közül

α > β

, akkor

\begin{matrix} sin (α - β) = sin α \cdot sin (90^{\circ} - β) - sin (90^{\circ} - α) sin β . \end{matrix}

Bizonyítás. Mérjük az

α

és

β

szögeket az

A C

átmérő két egyazon oldalára, úgy hogy

C A B ∢ = α

és

C A D ∢ = β

legyen, akkor Ptolemaios tétele szerint:

\begin{matrix} B D \cdot A C = B C \cdot A D - A B \cdot C D . \end{matrix}

Ebből ismét

\begin{matrix} \frac{B D}{A C} = \frac{B C}{A C} \cdot \frac{A D}{A C} - \frac{A B}{A C} \cdot \frac{C D}{A C}, \end{matrix}

tehát:

\begin{matrix} sin (α - β) = sin α sin (90^{\circ} - β) - sin (90^{\circ} - α) sin β . \end{matrix}

α

hegyesszög, akkor

(90^{\circ} - α)

is az; ha

sin (90^{\circ} - α)

-t ismerjük, akkor meghatározhatjuk

(90^{\circ} - α)

-t és ebből

α

-t is. Azt mondhatjuk tehát, hogy

sin (90^{\circ} - α)

meghatározza az

α

-t és ebben a minőségben ezt az értéket az

α

szög cosinusának nevezzük:

\begin{matrix} cos α = sin (90^{\circ} - α) . \end{matrix}

Ez új jelölést bevezetve alaptételeink így alakulnak:

\begin{matrix} I . sin (α + β) = sin α cos β + cos α sin β, \end{matrix}

\begin{matrix} I I . sin (α - β) = sin α cos β - cos α sin β . \end{matrix}

III. alaptétel. Ha az

α

és

β

hegyesszögek összege ismét hegyesszög:

\begin{matrix} cos (α + β) = cos α cos β - sin α sin β . \end{matrix}

Bizonyítás.

\begin{matrix} cos (α + β) = sin [90^{\circ} - (α + β)] = sin [(90^{\circ} - α) - β] = \end{matrix}

\begin{matrix} = sin (90^{\circ} - α) cos β - cos (90^{\circ} - α) \cdot sin β, \end{matrix}

ámde

\begin{matrix} cos (90^{\circ} - α) = sin [(90^{\circ} - (90^{\circ} - α)] = sin α, \end{matrix}

tehát

\begin{matrix} cos (α + β) = cos α cos β - sin α sin β . \end{matrix}

IV. alaptétel. Ha az

α

és

β

hegyesszögek közül

α > β

, akkor

\begin{matrix} cos (α - β) = cos α cos β + sin α sin β . \end{matrix}

Bizonyítás.

\begin{matrix} cos (α - β) = sin [(90^{\circ} - α) + β] = sin (90^{\circ} - α) \cdot cos β + sin α \cdot sin β, \end{matrix}

tehát

\begin{matrix} cos (α - β) = cos α cos β + sin α sin β . \end{matrix}

Állapodjunk meg már most abban, hogy bármely szög függvényeit úgy akarjuk értelmezni, hogy az

I - I V

. alaptételek érvényben maradjanak. Bármely szögre nézve legyen tehát:

\begin{matrix} sin (α + β) = sin α cos β + cos α sin β, \end{matrix}

(I.)

\begin{matrix} sin (α - β) = sin α cos β - cos α sin β, \end{matrix}

(II.)

\begin{matrix} cos (α + β) = cos α cos β - sin α sin β, \end{matrix}

(III.)

\begin{matrix} cos (α - β) = cos α cos β + sin α sin β . \end{matrix}

(IV.)

α = β

, akkor (II)-ből:

sin α = 0

.
Ha (I)-ben

β = 0

, akkor:

sin α = sin α cos 0^{\circ}

,
vagyis

\begin{matrix} cos 0^{\circ} = 1. \end{matrix}

A (IV)-ből:

α = β

esetében:

cos 0 = sin^{2} α + cos^{2} α = 1

.
Ha

α = 0

, akkor (II)-ből:

sin (- β) = - sin β

és (IV)-ből

cos (- β) = cos β

.
Ha

α = β = 45^{\circ}

, akkor (I)-ből:

\begin{matrix} sin 90^{\circ} = 2 \cdot {(\frac{1}{\sqrt[]{2}})}^{2} = 1 és (III)-ból: cos 90^{\circ} = 0. \end{matrix}

α = 90^{\circ}

, akkor (II)-ből:

sin (90^{\circ} - β) = cos β

és (IV)-ből:

\begin{matrix} cos (90^{\circ} - β) = sin β . \end{matrix}

α = β = 90^{\circ}

, akkor (I)-ből:

sin 180^{\circ} = 0

és (III)-ból

\begin{matrix} cos 180^{\circ} = - 1. \end{matrix}

α = 180^{\circ}

, akkor (II)-ből:

sin (180^{\circ} - β) = sin β

és (IV)-ből:

\begin{matrix} cos (180^{\circ} - β) = - cos β . \end{matrix}

Ha valamely

2 r

sugarú körben az

a_{1}, a_{2}, ..., a_{n}

húroknak megfelelő kerületi szögek

a_{1}, a_{2}, ..., a_{n}

, akkor

\begin{matrix} a_{1} : a_{2} : a_{3} : ... : a_{n} = sin a_{1} : sin a_{2} : sin a_{3} : ... sin a_{n} . \end{matrix}

(A)

Ez a húrok sinustétele.
Háromszög esetén e tétel következtében

\begin{matrix} a : b : c = sin α sin β : sin γ . \end{matrix}

(A*)

Ha pl.

n

húr van adva, melyekkel szemben fekvő kerületi szögek közt

m

összefüggés van adva

(m < n + 1)

, akkor fennáll a következő

(n + m)

egyenlet:

\begin{matrix} a_{i} = 2 r sin a_{i}, (i = 1,2, ..., n) \end{matrix}

\begin{matrix} f_{k} (a_{1}, a_{2}, ..., a_{n}) = 0, (k (1. 2, ..., m) \end{matrix}

Eme

n + m

egyenlet

2 n + 1

adatot tartalmaz, tehát általában

n - m + 1

alkatrész megadása után a hiányzó

n + m

adat kiszámítható. Érdekes az az eset, ha

\begin{matrix} a = 2 r sin α, b = 2 r sin β, c = 2 r sin γ és α + β + γ = 180^{\circ} . \end{matrix}

Ez a négy egyenlet használható a háromszögek megoldásánál. Hogy a sinustétel hogyan nyerhető, már láttuk, még csak a Carnot-tételt akarom levezetni,

\begin{matrix} sin α = sin [180^{\circ} - (β + γ)] = sin (β + γ,) \end{matrix}

tehát

\begin{matrix} sin^{2} α = {[sin β cos γ + cos β sin γ]}^{2} = sin^{2} β (1 - sin^{2} γ) + \end{matrix}

\begin{matrix} + 2 sin β sin γ cos β cos γ + (1 - sin^{2} β) sin^{2} γ = \end{matrix}

\begin{matrix} = sin^{2} β + sin^{2} γ + 2 sin β sin γ (cos β cos γ - sin β sin γ) \end{matrix}

vagy

\begin{matrix} sin^{2} α = sin^{2} β + sin^{2} γ + 2 sin β sin γ cos (β + γ) \end{matrix}

és így

\begin{matrix} sin^{2} α = sin^{2} β + sin^{2} γ - 2 sin β sin γ cos α \end{matrix}

(B)

Ebböl ismét

4 r^{2}

-tel minden tagot szorozva:

\begin{matrix} a^{2} = b^{2} + c^{2} - 2 b c cos α . \end{matrix}

(B*)

Valójában tehát a Carnot-féle tétel három ‐együttvéve

180^{\circ}

-t kitevő ‐ szög szögfüggvényeinek összefüggését fejezi ki.
Derékszögű háromszög esetén a következő öt egyenlet áll rendelkezésünkre:

\begin{matrix} a = 2 r sin α, b = 2 r sin β, c = 2 r sin γ, \end{matrix}

\begin{matrix} α + β + γ = 180^{\circ}, γ = 90^{\circ}, \end{matrix}

tehát

\begin{matrix} c = 2 r \end{matrix}

és így az ismert tételek:

\begin{matrix} a = c sin α, b = c sin β = c cos α . \end{matrix}

Ezekből ismét

\begin{matrix} c = a \frac{1}{sin α}, c = b \frac{1}{cos α}, \end{matrix}

\begin{matrix} a = b \frac{sin α}{cos α}, b = a \frac{cos α}{sin α} . \end{matrix}

Szimmetria kedveért szokásos bevezetni a következő új szögfüggvényeket:

\begin{matrix} cosec α = \frac{1}{sin α}, \end{matrix}

\begin{matrix} sec α = \frac{1}{cos α}, \end{matrix}

\begin{matrix} tg α = \frac{sin α}{cos α}, \end{matrix}

\begin{matrix} ctg α = \frac{cos α}{sin α}, \end{matrix}

mely esetben derékszögű háromszögekben:

\begin{matrix} c = a \end{matrix}

A rendelkezésemre álló szűk hely miatt csak e vázlatot közölhettem és így csak azok tanulhatnak belőle, kik a trigonometriával már amúgy is foglalkoztak. Célom az volt, hogy a goniometriát és trigonometriát, mint a húrtan alkalmazásait mutassam be és közben az alapfogalmakat egész szigorúsággal állítsam oda.