Kezdőlap


Cím:	A sík és a gömb geometriájának megegyeztetése 2.
Szerző(k):	Lukhaub Gyula
Füzet:	1904/február, 117 - 120. oldal	PDF \| MathML
Témakör(ök):	Szakmai cikkek

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

$4^{\circ} .$ Hasonlítsuk össze a sík- és gömbháromszögtan sinus-tételét. A gömb-háromszögtan sinus-tétele:

\begin{matrix} sin a : sin b : sin c = sin α : sin β : sin γ . \end{matrix}

Ha a síkháromszög oldalait és szögeit a megfelelő betűkkel jelöljük, akkor:

\begin{matrix} a : b : c = sin α : sin β : sin γ . \end{matrix}

Hogy ezen két tételt megegyezésbe hozzuk, fogalmazzuk a sík-háromszögtan sinus-tételét más alakban.
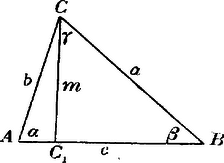
Ha az

A B C

háromszöget az

A B = c

oldal körül forgatjuk, akkor a

B C = a

oldal

C

végpontja ugyanazon kört írja le, mint a

C_{1} C = m

magasság

C

végpontja.
De

\begin{matrix} m = a sin β és 2 π m = 2 π a sin β . \end{matrix}

Ha bevezetjük a következő jelölést:

\begin{matrix} ◯ m = 2 π m, \end{matrix}

akkor

\begin{matrix} ◯ m = ◯ a \cdot sin β . \end{matrix}

Hasonlóképpen

\begin{matrix} ◯ m = ◯ b \cdot sin α; \end{matrix}

tehát

\begin{matrix} ◯ a : ◯ b = sin α : sin β . \end{matrix}

A sinus-tételt ennélfogva így is írhatjuk:

\begin{matrix} ◯ a : ◯ b : ◯ c = sin α : sin β : sin γ . \end{matrix}

Most térjünk át a gömbi sinus-tételre. Szorozzuk meg a baloldalt

2 π

-vel. Ekkor

\begin{matrix} 2 π sin a : 2 π sin b : 2 π sin c = sin α : sin β : sin γ . \end{matrix}

Ha a gömb sugara az egység, akkor

C O A ∢ = b

.
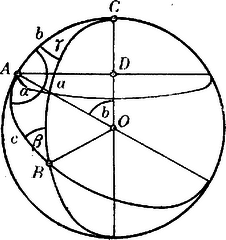
Bocsássunk

A

-ból a

C O

-ra az

A D

merőlegest.

\begin{matrix} A D = sin b . \end{matrix}

Forgassuk a gömböt a

C O

tengely körül, akkor az

A

pont egy párhuzamos vagy szélességi kört ír le, melynek sugara:

A D = sin b

.
Ugyanezen körnek gömbi sugara pedig

b

.
Tehát

\begin{matrix} 2 π sin b = ◯ b, \end{matrix}

hasonlóképpen

\begin{matrix} 2 π sin a = ◯ a, 2 π sin c = ◯ c . \end{matrix}

Ebből következik, hogy a gömbi sinus-tétel ilyen alakban formulázható:

\begin{matrix} ◯ a : ◯ b : ◯ a = sin α : sin β : sin γ, \end{matrix}

vagyis a sík- és gömb-trigonometriai sinus-tétel ilyen átalakítás mellett egymással megegyezik.

5^{\circ} .

Most térjünk át a sík- és gömb-trigonometria projekció-tételének összeegyeztetésére.
A projekció-télel a gömbön így szól:

\begin{matrix} cos b sin c = cos c sin b cos α + sin a cos β . \end{matrix}

Vizsgáljuk meg, hogy milyen jelentése van a

cos b

-nek és

cos c

-nek.
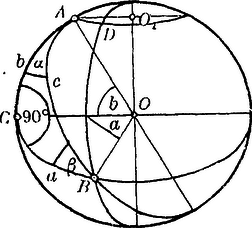
Rajzoljunk az

A

-ból kis kört, melynek síkja merőleges az

A C O

síkra. A

C B O

sík is merőleges az

A C O

síkra, úgy hogy az

A B C

háromszög derékszögű:

γ = \frac{π}{2}

Messük a gömböt egy a

B O

-n átmenő s a

C B O

síkra merőleges síkkal, mely a legnagyobb kört vágja ki, hol

D

ezen körnek és az

A

-ból rajzolt körnek metszéspontja.
Világos, hogy:

C O B ∢ = A O_{1} D ∢ = a

.
Határozzuk most meg az

\frac{{A D}_{}^{⌢}}{{C B}_{}^{⌢}}

viszonyt.
A kis kör sugara

\begin{matrix} A O_{1} = A O cos b = r cos b . \end{matrix}

Tehát

\begin{matrix} \frac{{A D}_{}^{⌢}}{{C B}_{}^{⌢}} = \frac{r cos b}{r} = cos b . \end{matrix}

Ebből láthatjuk, hogy egy tetszés szerinti általános gömbháromszög egyik oldalának cosinusa egyenlő az ezen oldal síkjára merőleges síkban fekvő kis kör ívdarabjának és az ezzel párhuzamos legnagyobb kör ugyanazon nyílású ívdarabjának a viszonyával, mely viszonyt a továbbiakban

v_{b}

akarjuk jelölni.
Tehát

\begin{matrix} v_{b} = cos b; \end{matrix}

éppen így:

\begin{matrix} v_{c} = cos c, v_{a} = cos a . \end{matrix}

Ennélfogva az általános gömbháromszögre vonatkozó projekció-tételt így is írhatjuk:

\begin{matrix} v_{b} sin c = v_{c} sin b cos α + sin a cos β . \end{matrix}

2 r π

-vel szorzunk, akkor, mint a sinus-tételnél:

\begin{matrix} ◯ c \cdot v_{b} = ◯ b \cdot v_{c} cos α + ◯ a \cdot cos β . \end{matrix}

Hasonlóképpen kapjuk, hogy

\begin{matrix} ◯ a \cdot v_{c} = ◯ c \cdot v_{a} cos β + ◯ b \cdot cos γ . \end{matrix}

\begin{matrix} ◯ b \cdot v_{a} = ◯ a \cdot v_{b} cos γ + ◯ c \cdot cos α . \end{matrix}

A síkban a projekció-tétel így szól:

\begin{matrix} c = b cos α + a cos β \end{matrix}

2 π

-vel szorozva:

\begin{matrix} ◯ c = ◯ b cos α + ◯ a cos β . \end{matrix}

Itt nem lép fel a

v_{b}

és

v_{c}

viszony. Ennek oka az, hogy a síkban

C B

és

A D

párhuzamos egyenesek, továbbá

A C

és

B D

az ezen egyenesekre merőleges egyenesek, s így
Ugyanezen oknál fogva :

\begin{matrix} v_{a} = v_{c} = 1. \end{matrix}

Tehát a síkbeli projekció-tételt szintén írhatjuk ezen alakban:

\begin{matrix} ◯ c \cdot v_{b} = ◯ \cdot cos v_{c} cos α + ◯ a \cdot cos β, stb . \end{matrix}

6^{\circ} .

Egyeztessük össze most azokat a képleteket a két geometriában, melyeket a félszögekre nyerünk, ha a háromszög három oldala van megadva.
Ismeretes, hogy

\begin{matrix} sin \frac{α}{2} = \sqrt[]{\frac{sin (s - b) sin (s - c)}{sin b sin c}}, \end{matrix}

\begin{matrix} cos \frac{α}{2} = \sqrt[]{\frac{sin s sin (s - a)}{sin b sin c}}, \end{matrix}

hol

\begin{matrix} 2 s = a + b + c . \end{matrix}

Hogy e képleteket összeegyeztethessük a sík-geometria megfelelő képleteivel, szorozzuk meg a jobboldalak számlálóit és nevezőit

4 r^{2} π^{2}

-tel, hol

r

a gömb sugara. Ekkor:

\begin{matrix} sin \frac{α}{2} = \sqrt[]{\frac{2 r π sin (s - b) sin (s - c)}{2 r π sin b \cdot 2 r π sin c}}, \end{matrix}

vagyis:

\begin{matrix} sin \frac{α}{2} = \sqrt[]{\frac{◯ (s - b) ◯ (s - c)}{◯ b \cdot ◯ c}}, \end{matrix}

\begin{matrix} cos \frac{α}{2} = \sqrt[]{\frac{◯ s \cdot ◯ (s - a)}{◯ b \cdot ◯ c}}, \end{matrix}

Hasonlóképpen járunk el a többi ilynemű képletekkel is.
A sík-geometriában az ezeknek megfelelő képletek a következők:

\begin{matrix} sin \frac{α}{2} = \sqrt[]{\frac{(s - b) (s - c)}{b c}}, \end{matrix}

\begin{matrix} cos \frac{α}{2} = \sqrt[]{\frac{s (s - a)}{b c}}, \end{matrix}

A jobb oldalt mindenütt

4 π^{2}

-tel szorozva és osztva, a következő alakban írhatjuk e formulákat:

\begin{matrix} sin \frac{α}{2} = \sqrt[]{\frac{◯ (s - b) ◯ (s - c)}{◯ b \cdot ◯ c}}, \end{matrix}

\begin{matrix} cos \frac{α}{2} = \sqrt[]{\frac{◯ s \cdot ◯ (s - a)}{◯ b \cdot ◯ c}}, \end{matrix}

Látjuk, hogy ezen formulák is alakilag teljesen megegyeznek a két geometriában.