Cím: A sík és a gömb geometriájának megegyeztetése 1.
Szerző(k):  Lukhaub Gyula 
Füzet: 1903/december, 57 - 62. oldal  PDF  |  MathML 
Témakör(ök): Szakmai cikkek

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

(I)

 
Ha összehasonlítjuk a sík- és gömbgeometria tételeit, azt találjuk, hogy némelyek teljesen megegyeznek a két geometriában, mások pedig nagyon hasonlók egymáshoz. A következőkben kimutatjuk, hogy e két geometria hasonló tételei a kellő fogalmazásban teljes megegyezésbe hozhatók.
1∘. Tudjuk, hogy a gömbháromszöget három legnagyobb kör határolja. Ha egység-sugarú gömböt veszünk alapul, akkor a gömbháromszög oldalainak mérőszámai ama testszöglet élszögeinek abszolut mérőszámai, melynek csúcsa a gömb középpontjában van, és melynek oldallapjai éppen a gömbháromszög három oldalát metszik ki. Ebből következik, hogy mindama tételek, melyek a háromélű testszöglet élszögeire érvényesek, helyesek a gömbháromszög oldalaira nézve is.
Tehát egyszerűen idézhetjük a következő ismert tételeket:
1. A gömbháromszög két oldalának összege nagyobb a harmadik oldalnál.
2. Egyenlő oldalakkal egyenlő szögek feküsznek szemben és viszont.
3. Nagyobb oldallal nagyobb szög fekszik szemben.
4. A szögek összege nagyobb π-nél, de kisebb 3π-nél.
Ha ezen tételeket összehasonlítjuk a síkgeometria megfelelő tételeivel, akkor azt találjuk, hogy a 1.2. és 3. tétel teljesen megegyezik a síkháromszög megfelelő tételével, míg a 4. nem egyezik meg, mert a háromszög szögeinek összege egyenlő π-vel. De ha a gömb sugara végtelen nagy lesz, akkor a gömbből sík, a gömbháromszögből síkháromszög lesz s ekkor a szögek összege: π.
Legyen ABC egy gömbháromszög. Fektessünk az A,B és C pontokon át síkot, mely a gömböt körben metszi. Ez a kör az ABC gömbháromszög köré írt kör. Határozzuk meg ennek a körnek a középpontját a gömbön.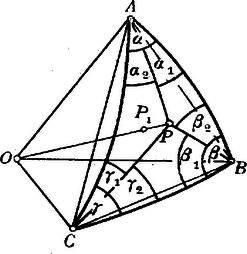
 
 

Evégből bocsássunk a gömbnek O középpontjából merőlegest az ABC síkra. E merőleges a síkot P1-ben, a gömböt P-ben döfi át. Az ABC síkháromszög köré írt kör középpontja: P1. Kimutatjuk, hogy e körnek középpontja a gömbön: P. Ugyanis:
OAP1≅OBP1Δ≅OCP1Δ,
tehát
AOP1∢=BOP1∢=COP1∢
s így az ezen szögekkel szemközt fekvő ívek is egyenlők, vagyis
AP⌢=BP⌢=CP⌢.
Tehát P egyenlő távolságra van az A,B és C pontoktól s így P az ABC köré írt kör középpontja, s AP⌢ ezen kör gömbi sugara. Ebből láthatjuk, hogy a gömbháromszög is éppen úgy bontható fel három egyenlőszárú gömbháromszögre, mint a síkháromszög három egyenlőszárú síkháromszögre.
Tegyük fel, hogy az A és B pontok szilárdak maradnak, de a C csúcs a köré írt kör kerületén mozog. Vajon állandó marad-e a C csúcsnál levő szög?
Legyenek a gömbháromszög szögei: α,β,γ; továbbá:
a2=CAP∢=ACP∢=γ1;γ2=BCP∢=CBP∢=β1;
β2=ABP∢=BAP∢=α1.
Ekkor:
α+β-γ=α1+α2+β1+β2-γ1-γ2,α+β-γ=α1+β2=2α1
állandó, mert a C változásával az α1 szög nem változik.
Itt azt látjuk, hogy ha a gömbháromszög egyik C csúcsa mozog, akkor nem változik az α+β-γ kifejezés.
A sík-geometriában a csúcsnál lévő szög állandó marad. De ha α',β',γ' egy síkháromszög szögei, akkor egyszersmind: α'+β'=π-γ' is állandó s így:
α'+β'-γ'=π-2γ'=állandó.
Tehát látjuk, hogy a sík-geometriában is érvényes az előbbi tétel.
Ez a tétel azért vezethető vissza a sík-geometriának ama tételére, hogy a csúcsnál levő szög állandó, mert itt tekintetbe vettük, hogy a szögek összege =π.
Hasonló tételt nyerünk akkor, ha a gömbháromszög egyik oldala változtatja helyzetét úgy, hogy a gömbháromszögbe írt kört folyton érintse.
Tegyük fel, hogy az ABC gömbháromszög AB=c oldala úgy mozog, hogy a beírt kört mindig érinti.
 
 

Ekkor:
a+b-c=CX+BX+CY+AY-AZ-BZ.
De:
CX=CY;BX=BZ;AY=AZ,
mert az egy pontból húzott érintők egyenlők. Ennélfogva:
a+b-c=CX+CY=2CX
állandó, minthogy c helyzetváltozásával a CX nem változik. Ez a tétel a síkháromszögre is érvényes s a bizonyítása is ugyanaz.
 
2∘. A gömbi négyszöget négy legnagyobb kör határolja.
Megvizsgáljuk, hogy a körbe és a kör köré írt négyszög szögeire, illetőleg oldalaira érvényesek-e a sík-geometriából ismert tételek.
Foglalkozzunk először a körbe írt gömbi négyszöggel.
Osszuk fel az ABCD gömbi négyszöget a BD legnagyobb körrel két gömbháromszögre.
 
 

Ekkor felírhatjuk mindegyik gömbháromszögre a következő egyenletet:
β'+δ'-α=2β2;β''+δ''-γ=-2β2;
az utóbbi egyenlet jobb oldalát negatív jellel vesszük, mert a BCD háromszög köré írt kör középpontja a háromszögön kívül fekszik.
Adjuk össze e két egyenletet:
β'+β''+δ'+δ''-α-γ=0,
de
β'+β''=βésδ'+δ''=δ,
tehát
β+δ=α+γ.

Ebből látjuk, hogy ha a gömbi négyszög körbe írható, akkor a szemben fekvő szögek összege egyenlő, éppen úgy mint a síknégyszögeknél. Csakhogy a gömbön ez az összeg nem egyenlő π-vel.
Hasonló tétel érvényes a kör köré írt gömbi négyszögre, csakhogy itt a szögek helyett az oldalak szerepelnek.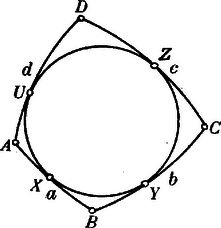
 
 

Ugyanis:
a+c=AX+BX+CZ+DZ=
=AU+BY+CY+DU=b+d.
Tehát a gömbi érintőnégyszögre is érvényes az ismert síkgeometriai tétel, hogy a szemközt fekvő oldalak összege egyenlő.
 
3∘. A Lexell-féle kör az olyan kör, mely a gömbháromszög egyik csúcsán és a másik két csúcs ellenpontján megy keresztül.
Legyen ABC az adott gömbháromszög. Ha A és B ellenpontjai A' és B', akkor a Lexell-féle kör az A'B' és C pontokon megy át.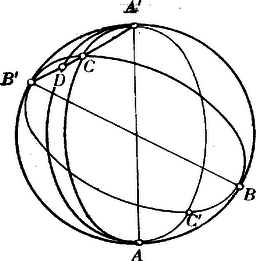
 
 

Legyen e kör gömbi átmérője A'D. Legyenek az ABC háromszög szögei α,β,γ; az A'B'C háromszög szögei α',β',γ'. Ekkor α'=π-α,β'=π-β,γ'=γ. Ha C a Lexell-féle kör kerületén mozog, akkor:
α'+β'-γ'=2α1=állandó.
De
α'+β'-γ'=π-α+π-β-γ=
=2π-(α+β+γ).

Vizsgáljuk meg ezen egyenlet geometriai értelmét.
Tudjuk, hogy a gömbháromszög területe:
T=r2(α+β+γ-π).
De 2π-(α+β+γ)=állandó, s így állandó ez a kifejezés is:
α+β+γ-π,
amiből következik, hogy ha az ABC gömbháromszög C csúcsa a Lexell-féle körön mozog, akkor e háromszög területe állandó.
A Lexell-féle kör felhasználásával kereshetjük azt a háromszöget, melynek két oldala adva van és melynek területe a legnagyobb.
Legyen az ABE gömbháromszög AB és AE oldala állandó hosszúságú. Legyen az AB szilárd s forogjon AE az A pont körül. Kérdés, hogy az AE milyen helyzete mellett lesz az ABE háromszög területe a lehető legnagyobb?
Az ABE háromszög területe:
T=r2(α+β+ϵ-π).
Szerkesszük meg az A'B'E Lexell-féle kört. Akkor:
2π-α-β-ϵ=2α1,α+β+ϵ-π=π-2α1
T maximum, ha ezen egyenlet baloldala a legnagyobb, vagyis ha α1 a legkisebb. Minthogy α1 negatív nem lehet, azért α1=0 mellett lesz T maximum. EkkorE összeesik a Lexell-féle kör A'D átmérőjének D végpontjával. Tehát annak a háromszögnek a területe a legnagyobb, melynek mozgó csúcsa a Lexell-féle kör A'-n keresztülmenő átmérőjének másik végpontjába esik.
Legyen ez a maximális területű háromszög ABD; hol: AD=AE.
Ekkor A'B'D a Lexell-féle körbe írt háromszög, melynek A'D, oldala a kör átmérője. Tehát:
α'+δ-β'=0;
vagyis:
π-α+δ-π+β=β+δ-α=0.
Ezen egyenlet pedig azt bizonyítja, hogy a maximális területű A'B'D háromszög olyan, hogy a köré írt kör átmérője BD, vagyis a harmadik változó oldal.
Vizsgáljuk most meg, hogy milyen tételek felelnek meg ezeknek a síkon.
Tegyük fel, hogy a gömb sugara a végtelenig nő, de úgy hogy az ABC pontok a végesben maradjanak. Az A',B' pontok a végtelenbe jutnak.
A Lexell-féle kör az AB oldal folytatását azonban az A',B' pontokban metszi s így a Lexell-féle kör olyan egyenessé lesz a végtelen sugarú gömbön, vagyis a síkon, mely az AB egyenest a végtelenben metszi, miből következik, hogy a Lexell-féle körnek a síkon az AB-vel párhuzamos és a C csúcson átmenő egyenes felel meg. Világos, hogy ha C ezen a párhuzamos egyenesen mozog, akkor az ABC háromszög területe állandó marad.
 
 

Ha AB és AC állandó, akkor az ABC háromszög területe akkor lesz a legnagyobb, ha: AB⊥AC, vagyis, ha az ABC háromszög köré írt kör átmérője a harmadik változó oldal BC.