Cím: A trieder
Szerző(k):  Lakner József, Petrozsény 
Füzet: 1904/április, 149 - 152. oldal  PDF  |  MathML 
Témakör(ök): Szakmai cikkek

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Egy P ponton átmenő 3 sugarat, melyek nem feküsznek egy síkban, a P pont 6 félsugárra osztja. Bármely ilyen 3 félsugár triédert alkot. A P pont a triéder csúcsa, a félsugarak a triéder élei. Két‐két él meghatároz egy élszöget és a triéder egy lapját, két lap pedig egy lapszöget. Az élszögek és lapszögek a triéder alkotórészei.
Ha a,b,c jelenti a triéder 3 élét, a∢,b∢,c∢, az a,b, ill. c élekhez tartozó 3 lapszöget, (ab)∢=γ,(ac)∢=β,(bc)∢=α a megfelelő 3 élszöget, akkor a térmértan ismert tételei szerint

0<α+β+γ<4R(1)
α+β>γ,α+β>β,β+γ>α.(2)
Minden triéderhez tartozik egy kiegészítő triéder, úgy, hogy
a+α1=2R,b+β1=2R,c+γ1=2R(3)
és
α+a1=2R,β+b1=2R,γ+c1=2R(4)
hol a1b1c1, ill. α1,β1γ1 a kiegészítő triéder lapszögeit ill. élszögeit jelenti.
Az (1) és (4) ill. (2) és (4)-ből a lapszögekre a következő határokat kapjuk:
2R<a1+b1+c1<6R(5)
hol természetesen az indexek el is hagyhatók. A triéder meg van határozva, ha alkotórészeiből három ismeretes. Így tehát a következő 6 eset különböztethető meg a triéderek megoldásánál.
(1). Ismeretes a három élszög: α,β,γ; meghatározandó a,b,c lapszög. Rajzoljuk egymás mellé a három élszöget. A két szélső élszöget ilyenkor úgy tekinthetjük, mintha le volnának forgatva a β síkjába az a ill. a c él körül. A b él tehát kétszer van leforgatva, egyszer a γ síkjával az a él körül, másodszor pedig az α síkjával a c él körü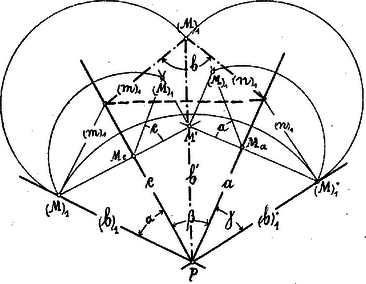l.
 
 

Válasszunk a kétszeresen leforgatott b élen egy tetszőleges M pontot, ill. ennek lefordításait (M)1 és (M)1+, és állítsuk elő M-nek képét a β síkon. M képe az (M)1-ból c-re és (M)1+-ből a-ra bocsátott merőlegesek metszőpontjában lesz. Ezek után, mint ismeretes, a c∢-et az M'Mc¯ befogóból és Mc(M1)¯ átfogóból szerkesztett derékszögű háromszögnek M1Mc¯ befogó mellett fekvő hegyes szöge adja. Épp így határozhatjuk meg az M'Ma¯ és Ma(M)1+¯ távolságok segélyével az a lapszöget. Hátra van még a b szög meghatározása. Ha tekintetbe vesszük, hogy a b∢-et az α ill. γ síkban fekvő és a b élre merőleges m,n egyenesek metszik ki, akkor ezeknek leforgatásait megkapjuk, ha (M)1-ben (b)1-re, ill. (M)1+-ben (b)1+-re merőlegest állítunk. Most már könnyen meghatározható az (mn) síknak nyomvonala és ezzel az m,n egyenesek alkotta b szög valódi nagysága.
(2). Ismeretes két élszög: α,β és az általuk bezárt lapszög. c él körül β síkjába forgatjuk az ismert α élszöget és a (b1)-en tetszőlegesen választott (M)1 pontnak c lapszög segítségével meghatározzuk M' képét; a P pontból, mint középpontból, P(M)1 távolsággal húzott körívnek és M'-ből a élre bocsátott merőlegesnek metszőpontja adja (M)1+-t. A további eljárás megegyezik az ismertetett elvekkel.
(3). Ismeretes két élszög: α és β és a nagyobbikkal átellenes lapszög a. β síkjába forgatjuk α-t és c élre merőleges segédképsíkot választunk, melyet 2-ik képsíknak fogunk tekinteni. Az ismert a lapszög segítségével meghatározzuk a γ sík második nyomvonalát és az α síknak c él mint első nyomvonal körül való felállításával meghatározhatjuk b él második nyompontját és ezzel b-nek első és második képét. Ezek után a többi alkotórészek meghatározása nem ütközik nehézségbe.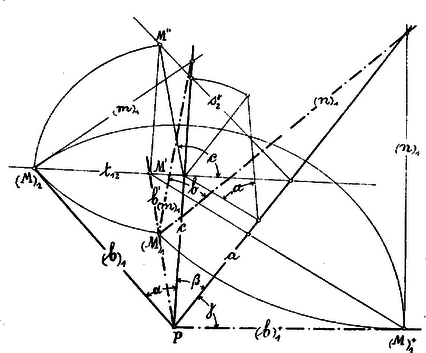
 
 

(4). Ismeretes két lapszög: a és c és ezen élek által bezárt β élszög; meghatározandók a többi alkotórészek. A b élen tetszőlegesen választott M pontnak M' vetületéből, mint középpontból, r1=MM'¯ctga és r2=MM'¯ctgc radiusszal két koncentrikus kört rajzolunk. Az r1 sugarú körhöz vont érintő lesz a triéder a éle; a élt adott β szög alatt metsző és r2 sugarú kört érintő egyenes lesz a c él. Az a,c élek metszőpontja meghatározza a triéder 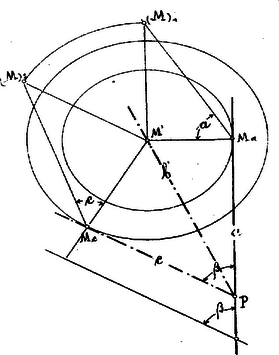P csúcsát.
 
 

(5). Ismeretes két lapszög: a és b és az egyikkel szemben fekvő α élszög; meghatározandó a triéder többi alkotórésze. γ síkjába b él körül leforgatjuk az a oldallapot és b lapszög segítségével c él M pontjának meghatározzuk a képét a γ síkon, M' pontból, mint középpontból, r=MM'ctga radiusszal kört rajzolunk; P pontból e körhöz vont érintője adja az 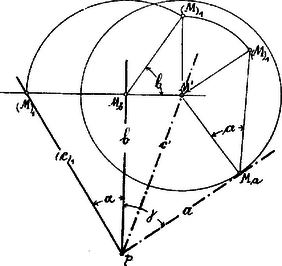a élt.
 
 

(6). Ismeretes a három lapszög; meghatározandó a triéder három élszöge. E feladat a kiegészítő triéder segítségével az (1)-ben ismertetett elvek alapján oldható meg, mit az olvasóra bízok.
A most tárgyalt feladatoknak bizonyos esetekben két megoldásuk van, de ezek fejtegetésére a jelen alkalommal nem szándékozom kiterjeszkedni.
Triéder megoldások körébe számos példa tartozik; ezek közül nehányat gyakorlásul közlök:
 
XCIV. Adva van két sík első nyomvonala: s'1,s12; és azon két szög, melyet a két sík metsző egyenese s'1 ill. s12-vel alkot; meghatározandó a két sík második nyomvonala.
 
XCV. Adva van egy egyenes körkúp; tengelye merőleges az első képsíkra és egy L pont; meghatározandó az L-en átmenő két érintősík (φ) hajlásszöge.
 
XCVI. Adva van g és l torzegyenespár; meghatározandó azon transzverzális, mely g-vel α, l-el β szögöt zár be.
 
XCVII. Adva van g általános helyzetű egyenes és kívüle P pont; meghatározandó azon t egyenes, mely t12-vel és g-vel adott szögeket zár be.
 
XCVIII. Adva van egy sík; meghatározandó e síkban oly l egyenes, mely egy az első képsíkban fekvő g egyenest adott α szögben metsz.
 
XCIX. Adva van az első felező síkban fekvő P pont; meghatározandó a P-n átmenő s sík úgy, hogy első képsíkszöge α és első és második nyomvonala által képezett szöge β legyen.
Petrozsény.