Kezdőlap


Cím:	Vázlatok a mathematika történetéből (Ptolemaios) 3.
Szerző(k):	Baumgartner Alajos
Füzet:	1903/február, 149 - 152. oldal	PDF \| MathML
Témakör(ök):	Egyéb írások

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Ptolemaios 3.

Az "Almagest".

A X. fejezet egy nagyon egyszerű készüléket ír le, mely a Nap magasságának meghatározására szolgál annak delelésekor. A XI. fejezet, melynek czíme körülbelül ez: "Bevezető tételek a gömbi tárgyalásokhoz" ismét kiválóan fontos és érdekes tételeket vezet le. Az első ezek közül így szól: ha két (

A B

és

A Γ)

egyeneshez más kettőt

(B E

és

Γ Δ)

húzunk, melyek egymást

Z

pontban metszik, akkor

Γ A

és

A E

aránya

Γ Δ

és

Z Δ

meg

Z B

és

B E

arányából tevődik össze.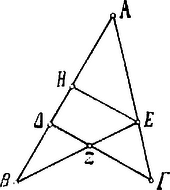

Ez azt jelenti, hogy

\begin{matrix} \frac{Γ A}{A E} = \frac{Γ Δ}{Z Δ} \cdot \frac{Z B}{B E}, \end{matrix}

(1)

a miből:

\begin{matrix} A E \cdot Γ Δ \cdot Z B = Γ A \cdot Z Δ \cdot B E . \end{matrix}

Ptolemaios a tétel bizonyítását is adja.
Meghúzza a

Γ Δ

-val párhuzamos

E H

segédvonalat, miáltal ezeket az aránylatokat kapja: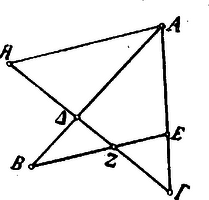

\begin{matrix} Γ A : E A = Γ Δ : E H \end{matrix}

és

\begin{matrix} B Z : B E = Z Δ : E H . \end{matrix}

Ez aránylatokból

\begin{matrix} E H = \frac{E A \cdot Γ Δ}{Γ Δ} \end{matrix}

és

\begin{matrix} E H = \frac{B E \cdot Z Δ}{B Z}, \end{matrix}

\begin{matrix} \frac{E A \cdot Γ Δ}{Γ Δ} = \frac{B E \cdot Z Δ}{B Z} \end{matrix}

a miből rendezés után máris megkapjuk a bebizonyítandó tételt.

Ptolemaios ugyanezekre az egyenesekre hasonló módon (ez esetben az

A

pontból a

B E

-vel párhuzamosan vont

A H

segédvonal révén) egy másik tételt vezet le:

\begin{matrix} \frac{Γ E}{E A} = \frac{Γ Z}{Δ Z} \cdot \frac{Δ B}{B A} \end{matrix}

(2)

vagy:

\begin{matrix} E A \cdot Γ Z \cdot Δ B = Γ E \cdot Δ Z \cdot B A . \end{matrix}

Egy harmadik levezetése a következő: legyen egy kör középpontja

Δ

és a kör kerületén három pont:

A, B

és

Γ

. Kössük össze

A

és

Γ

pontokat és vonjuk meg

B

és

Δ

pontokon át az átmérőt. E két vonal

E

pontban metszi egymást. Rajzoljuk meg az

A

és

Γ

pontokból az átmérőre bocsátott

A Z

és

Γ H

merőlegeseket; ekkor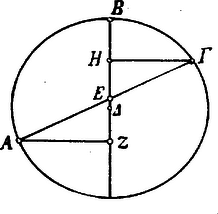

\begin{matrix} A Z : Γ H = A E : E Γ . \end{matrix}

"De ugyanaz az arány van

A Z

és

Γ H

között, mint az

A B

kétszeres ívéhez tartozó húr és a

B Γ

kétszeres ívéhez tartozó húr között. Mert a merőlegesek e húrok e. Tehát az arány

A E

és

E Γ

között ugyanaz, mint az

A B

kétszeres ívéhez tartozó húr és a

Γ

kétszeres ívéhez tartozó húr között". (3)
Nem szabad többé elsiklanunk e kifejezés fölött, mellyel a mathematika történetében immár másodszor találkozunk: a kétszeres ívhez tartozó húr; első ízben a Menelaos-féle tételnek gömbháromszögre való kiterjesztésénél tűnt fel (K. M. L. IX. évf. 222. l.). Tudjuk, hogy a kör sugarához viszonyítva ennek a húrnak a fele nem egyéb, mint a húrhoz tartozó középponti szög felének a sinusa. Ennélfogva nem túlságos merész az az állítás, hogy a goniometria lényege már a görögök mathematikájában bukkan fel és hogy inkább csak a szavak, az elnevezések hiánya miatt nem ismerjük fel rögtön, első pillantásra. A legutóbb tárgyalt aránylat mai jelöléseinkkel tehát ez: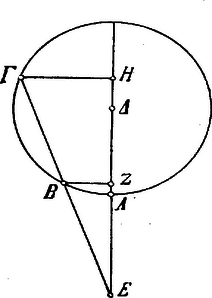

\begin{matrix} A E : E Γ = sin \hat{A B} : sin \hat{B Γ} . \end{matrix}

A következő tételt arra az esetre bizonyítja be, a mikor az

E

pont a körön kívül esik: ekkor "a

Γ A

kétszeres ívéhez tartozó húr úgy aránylik az

A B

kétszeres ívéhez tartozó húrhoz. mint

Γ E

E B

-hoz" ...

(4)

vagyis:

\begin{matrix} sin \hat{Γ A} : sin \hat{A B} = Γ E : E B . \end{matrix}

Ezekkel a tételekkel most már követhetjük Ptolemaiost gömbháromszögtani fejtegetéseibe is. Ezeket így vezeti be: rajzoljunk egy gömb felületére különböző íveket (ld. ábra), melyek legnagyobb körökhöz tartoznak; legyenek ezek

A B

és

A Γ

ívek, melyek a

B E

és

Γ Δ

íveket metszik;

B E

és

Γ Δ

ívek

Z

pontban metszik egymást.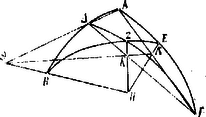

Ekkor "a

Γ E

kétszeres ívéhez tartozó húr aránya az

E A

kétszeres ívéhez tartozó húrhoz összetevődik a

Γ Z

kétszeres ívéhez tartozó húrnak meg a

Z Δ

kétszeres ívéhez tartozó húrnak arányából és a

Δ B

kétszeres ívéhez tartozó húrnak meg a

B A

kétszeres ívéhez tartozó húrnak arányából."
"Mert legyen

H

a gömb középpontja és húzzuk meg e pontból a

B, Z

és

E

pontokhoz, melyek ugyanegy körön feküsznek, az

H B, H Z

és

H E

egyeneseket. Húzzuk meg az

A Δ

egyenest, a mely meghosszabbítva

H B

meghosszabbítását

Θ

pontban metszi. Húzzuk meg a

Δ Γ

és

A Γ

húrokat, melyek megfelelően

H Z

-t

K

pontban és

H E

-t

A

pontban metszik. A

Θ

K

és

A

pontok egy egyenesben feküsznek. Ugyanis mind a három egyidejűleg két síkban fekszik: az

A Γ Δ

háromszög és a

B Z E

kör síkjában. Így azután a

Θ Δ

és

Γ Δ

egyenesek

K

pontban metszik egymást. Ennélfogva:

\begin{matrix} \frac{Γ Δ}{Δ A} = \frac{Γ K}{K Δ} \cdot \frac{Δ Θ}{Θ A} . \end{matrix}

De a miképpen

Γ A

aránylik

Δ A

-hoz, úgy aránylik

Γ E

kétszeres ívéhez tartozó húr az

E A

kétszeres ívéhez tartozó húrhoz.^{$^{*}$} És

Γ K

úgy aránylik

K Δ

-hez, mint a

Γ Z

kétszeres ívéhez tartozó húr a

Z Δ

kétszeres ívéhez tartozó húrhoz. De még

Δ Θ

úgy aránylik

Θ

-hoz, mint a

Δ B

kétszeres ívéhez tartozó húr a

B A

kétszeres ívéhez tartozó húrhoz."^{$^{*}$} Ezekből pedig már következik az a tétel, melyet Ptolemaios e gömbháromszögtani fejtegetés elején kimondott és a mely mai goniometriai jelöléseinkkel ily alakú:

\begin{matrix} \frac{sin Γ E}{sin E A} = \frac{sin Γ Z}{sin Z Δ} \cdot \frac{sin Δ B}{sin B A} \end{matrix}

(5)

A fejezet végén még egy hasonló összefüggés van:

\begin{matrix} \frac{sin Γ A}{sin E A} = \frac{sin Γ Δ}{sin Δ Z} \cdot \frac{sin Z B}{sin B E} \end{matrix}

(6)

^*A(2)egyenletalapján;l.150.lap.

^{$^{*}$} A (3) tétel alapján; l. 151. lap.

^{$^{*}$} A (4) tétel alapján; l. 151. lap.