Cím:	Vázlatok a mathematika történetéből (Ptolemaios) 2.
Szerző(k):	Baumgartner Alajos
Füzet:	1902/december, 82 - 88. oldal	PDF  |  MathML
Témakör(ök):	Egyéb írások

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. Ptolemaios.   Az ,,Almagest".   A IX. fejezet czíme: A körbe írt egyenesek értékéről. Rendkívül érdekes és fontos fejezet ez, mert nem egyéb, mint egy rendszeres goniometriai táblázat, melyet a kiszámításához szükséges elméleti vonatkozások előznek meg. Minden hosszadalmas magyarázat helyett legczélszerűbb magát a szerzőt megszólaltatni: ,,A gyakorlat könnyebbsége végett egy táblázatot állítunk össze ez egyenesek értékéről, miközben a kerületet $360$ fokra osztjuk fel. Táblázatunknak összes ívei fél fokkal növekednek, állandóan, és mi megadjuk ez ívek mindegyikéhez a húr értékét, azzal a föltevéssel, hogy az átmérőt $120$ részre osztottuk fel. A használat révén látni fogjuk, hogy ez a szám a legkényelmesebb, melyet választani lehet. Megmutatjuk előbb, miképpen készül oly tételek lehető legkisebb számának segítségével, melyek mindig ugyanazok, általános és pontos módszer amaz értékek meghatározására. Nem szorítkozunk azonban erre a táblázatra, a melyből ez értékeket kivehetjük, az elmélet ismerete nélkül, de megkönnyítjük az eszközöket, hogy azokat kipróbáljuk és igazoljuk, megadva a szerkesztési módszereket. Általánosságban a hatvanas számozást használjuk, hogy elkerüljük a törtek bonyodalmasságát; és a szorzásokban és osztásokban mindig a legmegközelítőbb eredményeket vesszük, oly módon, hogy az, a mit elhanyagolunk, nem zavarja meg azok pontosságát." Ezek után minden átmenet nélkül meghatározza a körbe írt szabályos ötszög és szabályos tízszög oldalát, oly módon, hogy a kör sugarának $E$ felező pontjából ($1$. ábra) az $EB$ hosszúságot az átmérőre leforgatja $EZ$-be és kimutatja, hogy $Z\Delta$ a szabályos tízszög és $ZB$ a szabályos ötszög oldala. 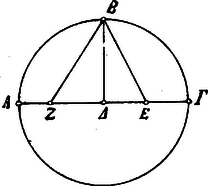    Most következik a legérdekesebb részek egyike: a goniometriai értékek kiszámítása. Ez a rész mindenekfölött arra érdemes, hogy szó szerint ismertessük e helyen: ,,Miután, mint mondottam, a kör átmérőjét felosztottuk 120 részre, $\Delta E$, mely a sugár fele, $30$ résznyi és négyzete $900$. A $B\Delta$ sugár, $60$ résznyi és négyzete $3600$; de $EB$, vagyis $EZ$ négyzete $4500$: következőleg ennek az $EZ$ vonalnak hossza $\xi \overline{\zeta }\delta \text{'}\epsilon \text{'}\text{'}(67$ egész $\frac{4}{60}$ és $\frac{55}{3600}$ rész) és így $\Delta Z$-nek a hossza $\lambda \overline{\zeta }\delta \text{'}\nu \epsilon \text{'}\text{'}(37$ egész $\frac{4}{60}$ és $\frac{55}{3600}$ rész). Továbbá, mivel $\Delta Z$ maga $3\overline{7}4\text{'}55\text{'}\text{'}$, négyzete $137\overline{5}4\text{'}15\text{'}\text{'}$; de $\Delta B$ négyzete $3600$ és e két négyzet összege egyenlő $BZ$ négyzetével, mely ennélfogva $497\overline{5}4\text{'}15\text{'}\text{'}$, tehát $BZ$ maga $7\overline{0}32\text{'}3\text{'}\text{'}$. Nyilvánvaló, hogy a szabályos hatszög oldala, mely ${60}^{\circ }$-ú ívet befog és mely a sugárral egyenlő, $60$ részt foglal magában. Éppen így a négyzet oldalának, mely a kerületnek ${90}^{\circ }$-ját fogja be, a négyzete kétszerese a sugár négyzetének; és a háromszög oldalának, mely ${120}^{\circ }$ -ot fog be, a négyzete háromszorosa a sugár négyzetének. De a sugár négyzete $3600$ és így a négyzet oldalának négyzete $7200$, a háromszög oldaláé pedig $10800$. Ennélfogva az az oldal, mely a kerületnek ${90}^{\circ }$-ját fogja be, $8\overline{4}51\text{'}10\text{'}\text{'}$ és az az oldal, mely ${120}^{\circ }$ -ot fog be, $10\overline{3}55\text{'}23\text{'}\text{'}$ résznyi hosszú." Ezek után hasonló módon kiszámitja még a ${144}^{\circ }$-ú ívhez tartorzó húrt, melyet $11\overline{4}7\text{'}37\text{'}\text{'}$ hosszúnak talál, azután egyéb húrok kiszámítása czéljából áttér a körbe írt négyszög tárgyalására és ennek folyamán levezeti azt a nevezetes tételt, mely Ptolemaios nevével kapcsolatosan ismeretes. E tétel is arra érdemes mathemtikai fontosságánál és történeti érdekességénél fogva, hogy levezetését egész terjedelmében közöljük: ,,Legyen a körbe írt tetszőleges négyszög $AB\Gamma \Delta$; húzzuk meg az átlóit: $A\Gamma$ és $B\Delta$. Be kell bizonyítani, hogy az $A\Gamma$ és $B\Delta$ vonalokkal megszerkesztett téglalap egyenlő az $AB$ és $\Gamma \Delta$ meg az $A\Delta$ és $B\Gamma$ szembenfekvő oldalakkal megszerkesztett téglalapokkal (mai kifejezéseinkkel: 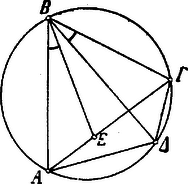$A\Gamma \cdot B\Delta =AB\cdot \Gamma \Delta +A\Delta \cdot B\Gamma )$.     Legyen $ABE$ szög akkora, mint $\Delta B\Gamma$. Ha mindegyikhez hozzácsatoljuk a közös $EB\Delta$ szöget, az $AB\Delta$ szög akkora lesz, mint az $EB\Gamma$ szög. De $B\Delta A$ és $B\Gamma E$ szögek egyenlők egymással, mert ugyanazon az íven nyugvó kerületi szögek. Tehát az $AB\Delta$ és $B\Gamma E$ háromszögek egyenlő szögűek. Ennélfogva $B\Gamma$ úgy aránylik a $\Gamma E$-hoz, mint $B\Delta$ a $\Delta A$-hoz. Így $B\Gamma A\Delta$ (értsd: $B\Gamma \cdot A\Delta$) annyi, mint $B\Delta \cdot \Gamma E$. Továbbá, mivel $ABE$ szög egyenlő $\Delta B\Gamma$ szöggel és $BAE$ szög egyenlő $B\Delta \Gamma$ szöggel, az $ABE$ és $B\Gamma \Delta$ háromszögek is egyenlő szögűek; ennélfogva $BA$ úgy aránylik az $AE$-hez, mint $B\Delta$ a $\Delta \Gamma$-hoz. Így $BA\cdot \Delta \Gamma$ annyi, mint $B\Delta \cdot AE$. Kimutattuk tehát, hogy $B\Gamma \cdot A\Delta$ akkora, mint $B\Delta \cdot \Gamma E$. Következőleg az egész $A\Gamma B\Delta$ négyszög akkora, mint az $AB\Delta \Gamma$ és $A\Delta B\Gamma$ négyszögek. Ezt kellett kimutatni." Hogy mi czélból volt szüksége Ptolemaiosnak erre a tételre, az a következőkből derül ki. A körbe írt négyszög egyik oldalának a kör átmérőjét $(A\Delta$) veszi, másik két oldalának pedig oly húrokat, melyeket már ismer, pl. $AB$ és $A\Gamma$ húrokat. Mivel tehát most már az $AB\Gamma \Delta$ húrnégyszögnek két átlóját és három oldalát ismeri, kiszámíthatja a $B\Gamma$ ívhez tartozó $B\Gamma$ húr hosszát is. Így egyebek között a $72{}^{\circ }$-ú és $12{}^{\circ }$-ú ívekhez tartozó húrokból a $12{}^{\circ }$-ú ívhez tartozó húrt. 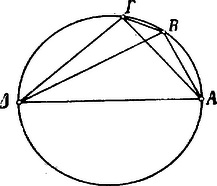 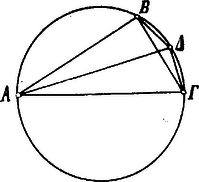     Továbbá meg tudja határozni egy kis segédszerkesztéssel a $B\Gamma$ ívhez tartozó ismert $B\Gamma$ húrból a $\frac{B\Gamma }{2}$ ívhez tartozó $\Delta \Gamma$ húr nagyságát is. ,,Így például a $12{}^{\circ }$-ú szöghöz tartozó húrból megtaláljuk a $6^{\circ }$-ú, a $3^{\circ }$-ú, az $1{\frac{1}{2}}^{\circ }$-ú és a ${\frac{3}{4}}^{\circ }$-ú ívhez tartozó húrokat. A számítás által azt találjuk, hogy az $1{\frac{1}{2}}^{\circ }$-ú ívhez tartozó húr $\overline{1}34\text{'}15\text{'}\text{'}$ és a ${\frac{3}{4}}^{\circ }$-hoz tartozó húr $047\text{'}8\text{'}\text{'}$." Végre pedig, miután két szöghöz tartozó húrokból kiszámította az e szögek összegéhez tartozó húr nagyságát, a nagyon kis szögekhez: az $1^{\circ }$‐ és ${\frac{1}{2}}^{\circ }$-ú szögekhez tartozó húrokat határozza meg, ez esetben már egyszerű arányosság révén. És most mindezek után következik maga a táblázat, az ókori mathematikai munkálkodásnak egyik legérdekesebb és legbecsesebb gyümölcse. Mivel az Almagest kiadásához meglehetősen ritkán lehet csak hozzá férni, a táblázat pedig nagyon is arra érdemes, hogy megismerjük, nem tartom fölösleges dolognak, hogy egyes töredékeit e helyen bemutassam. Itt közlöm a táblázat kezdetét, mellette a magyar fordítását, illetőleg mai számainkkal való értelmezését: 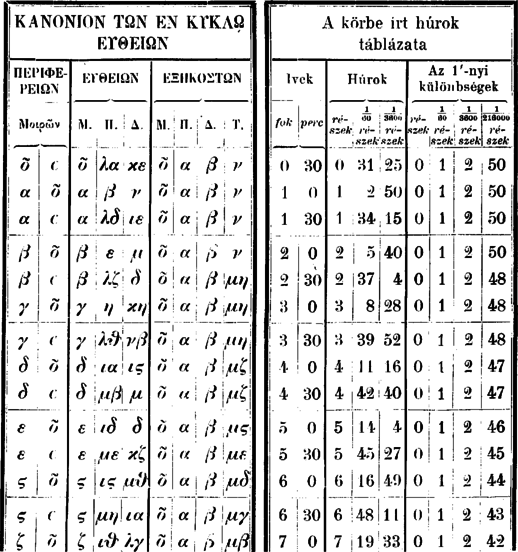    A második rovatban találhat $c$ jel, mint a görög $\alpha$ betű fele, $\frac{1}{2}$ fokot jelent. Nem tartjuk érdektelen vagy hiábavaló dolognak, ha kissé mélyebben bocsátkozunk e táblázat fejtegetésébe és egy-egy adatának utána számításába. A táblázat első sora megadja a $0^{\circ }30\text{'}$-nyi ívhez tartozó húr nagyságát az átmérő $\frac{1}{120}$ részeiben kifejezve, mint a hogy minden sor az általános $\phi$ szöghöz tartozó húr: $\begin{array}{c}{\displaystyle a=2r\cdot \text{sin}\frac{\phi }{2}=120\cdot \text{sin}\frac{\phi }{2}}\end{array}$ nagyságát adja meg. Ennélfogva az első sorbeli húr értéke: $\begin{array}{c}{\displaystyle a={120}^{\circ }30\text{'}\text{sin}{}^{\circ }15\text{'}=120\cdot \mathrm{0,0043635}=}\end{array}$ $\begin{array}{c}{\displaystyle =\mathrm{0,52362}=31\left(\frac{1}{60}\right)+25\left(\frac{1}{36000}\right)\mathrm{,}}\end{array}$ tehát csakugyan $\delta \lambda \alpha \text{'}\chi \epsilon \text{'}\text{'}$, a mint Ptolemaios a szövegben jelölte. Mivel pedig látja, hogy kis szögekhez tartozó húrok korlátolt pontossággal arányosak a szögekkel (hiszen még a $2^{\circ }$-ú szöghöz tartozó húr $\overline{2}5\text{'}40\text{'}\text{'}$ is kétszer akkora, mint az $2^{\circ }$-ú szöghöz tartozó húr: $\overline{1}2\text{'}50\text{'}\text{'}$), bátran térhet át a $0^{\circ }30\text{'}$-nél kisebb szögekhez tartozó húrokra egyszerű arányosság útján. Ha tehát a $0^{\circ }30\text{'}$-nyi szöghöz tartozó húr: $\overline{0}31\text{'}25\text{'}\text{'}=\mathrm{0,52362}$ értékét elosztja $30$-cal, megkapja az $1\text{'}$-nyi szöghöz tartozó húr nagyságát ez értékben: $\begin{array}{c}{\displaystyle \mathrm{0,017454}=1\left(\frac{1}{60}\right)+2\left(\frac{1}{3600}\right)+50\left(\frac{1}{216000}\right)\mathrm{,}}\end{array}$ a mint azt a táblázatban csakugyan így meg is találjuk. Ugyane rovat többi sorai pedig szintén arányos részek, melyek szerint a kis szögkülönbségekhez tartozó húrkülönbségek korlátolt pontossággal változnak. Ezek tehát egyszerűen az $1\text{'}$-hez tartozó arányos részek, mint a milyeneket a mi logarithmus-könyveinkben is találunk. Ptolemaios táblázatát tovább kísérve, még a következő nevezetesebb szögekhez tartozó húrokat említhetjük meg:   ${\displaystyle \begin{array}{|ccccccccc|}\hline \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>ξ</mi></math>}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>δ</mi></math>}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>ξ</mi></math>}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>δ</mi></math>}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>δ</mi></math>}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>δ</mi></math>}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>δ</mi></math>}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>ν</mi><mi>δ</mi></math>}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>ϰ</mi><mi>α</mi></math> }}\hfill \\ \hline\end{array}}$  ${\displaystyle \begin{array}{|ccccccccc|}\hline \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mn>60</mn></math>}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mn>0</mn></math>}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mn>60</mn></math>}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mn>0</mn></math>}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mn>0</mn></math>}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mn>0</mn></math>}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mn>0</mn></math>}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mn>54</mn></math>}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mn>21</mn></math> }}\hfill \\ \hline\end{array}}$   mert a ${60}^{\circ }$-ú szöghöz tartozó húr akkora, mint a sugár, tehát $60$ egység; érdekesebb sor továbbá ez:   ${\displaystyle \begin{array}{|ccccccccc|}\hline \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>ζ</mi></math>}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>δ</mi></math>}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>π</mi><mi>δ</mi></math>}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>ν</mi><mi>α</mi></math>}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>ι</mi></math>}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>δ</mi></math>}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>δ</mi></math>}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>μ</mi><mi>δ</mi></math>}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>ϰ</mi></math> }}\hfill \\ \hline\end{array}}$  ${\displaystyle \begin{array}{|ccccccccc|}\hline \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mn>90</mn></math>}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mn>0</mn></math>}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mn>84</mn></math>}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mn>51</mn></math>}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mn>10</mn></math>}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mn>0</mn></math>}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mn>0</mn></math>}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mn>44</mn></math>}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mn>20</mn></math> }}\hfill \\ \hline\end{array}}$ mert a ${90}^{\circ }$-ú szöghöz tartozó húrnak, vagyis a körbe irt négyzet oldalának nagysága $\begin{array}{c}{\displaystyle r\sqrt[]{2}=60\cdot \mathrm{1,414213}=84+51\left(\frac{1}{60}\right)+10\left(\frac{1}{3600}\right)\mathrm{.}}\end{array}$ Végre pedig a táblázat utolsó sora ez:   ${\displaystyle \begin{array}{|ccccccccc|}\hline \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>ϱ</mi><mi>π</mi></math>}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>δ</mi></math>}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>ϱ</mi><mi>ϰ</mi></math>}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>δ</mi></math>}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>δ</mi></math>}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>δ</mi></math>}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>δ</mi></math>}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>δ</mi></math>}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>δ</mi></math> }}\hfill \\ \hline\end{array}}$  ${\displaystyle \begin{array}{|ccccccccc|}\hline \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mn>180</mn></math>}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mn>0</mn></math>}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mn>120</mn></math>}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mn>0</mn></math>}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mn>10</mn></math>}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mn>0</mn></math>}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mn>0</mn></math>}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mn>0</mn></math>}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mn>0</mn></math> }}\hfill \\ \hline\end{array}}$ mert a ${180}^{\circ }$-ú szöghöz tartozó húr maga az átmérő, vagyis $120$ egység. Mindezekből azt látjuk, hogy Ptolemaios táblázatának tartalma nem egyéb, mint a szögek sinusai, melyeknek értékei az iskolai logarithmus-könyvekben rendesen a II. táblázatban megvannak. Hiszen a Ptolemaios-féle táblázatból minden szög sinusát lehet kiszámitani: Ptolemaios-féle adatot csak el kell osztani $120$-szal és megvan az illető szög felének a sinusa.