Kezdőlap


Cím:	A kúpnak metszése az alappal nem párhuzamos síkokkal
Szerző(k):	Szimányi Samu
Füzet:	1902/április, 200 - 203. oldal	PDF \| MathML
Témakör(ök):	Szakmai cikkek

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Ha egy egyenes kúpot az alappal nem párhuzamos síkkal úgy metszünk, hogy a metszet ellipsis és ha $p$ és $q$ a nagy tengely távolságai a kúp csúcsától, $α$ a kúp oldalvonalai áltat bezárt szög; ha továbbá az ellipsis fél nagy tengelye $a$ , a fél kis tengelye 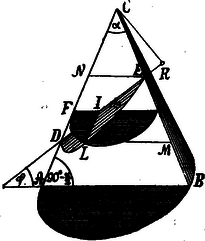$b$ , akkor

\begin{matrix} b = \sqrt[]{p q \cdot sin \frac{α}{2}}, \end{matrix}

az excentricitás

\begin{matrix} e = \frac{p - q}{2} \end{matrix}

és a lemetszett darab köbtartalma:

\begin{matrix} k = \frac{π {(p q)}^{\frac{3}{2}} sin^{2} \frac{α}{2} cos \frac{α}{2}}{3} . \end{matrix}

Legyen

A B C

a kúp tengelymetszete,

\begin{matrix} A C = s; \end{matrix}

Felezzük

D E

-t úgy, hogy

D I = I E

és fektessünk

I

ponton át az alappal párhuzamos síkot, akkor ezen sík az

A B C

síkon merőlegesen áll; ennélfogva

\begin{matrix} I L ⊥ D E \end{matrix}

továbbá

\begin{matrix} C D : D M = A C : A B vagy p : D M = s : 2 r \end{matrix}

miből

\begin{matrix} D M = \frac{2 p r}{s} hasonlóképpen E N = \frac{2 q r}{s}, \end{matrix}

továbbá

\begin{matrix} I L^{2} = b^{2} = I G \cdot I F = \frac{p q r^{2}}{s^{2}}, \end{matrix}

tehát

\begin{matrix} b = \frac{r}{s} \sqrt[]{p q}, de \frac{r}{s} = sin \frac{α}{2} \end{matrix}

s így

\begin{matrix} b = \sqrt[]{p q} \cdot sin \frac{α}{2} . \end{matrix}

Carnot tételét alkalmazva:

\begin{matrix} 4 a^{2} = p^{2} + q^{2} - 2 p q cos α = {(p - q)}^{2} + 2 p q (1 - cos α) \end{matrix}

\begin{matrix} 4 a^{2} = {(p - q)}^{2} + 4 p q sin^{2} \frac{α}{2}) \end{matrix}

és

\begin{matrix} a^{2} = {(\frac{p - q}{2})}^{2} + p q sin^{2} α = {(\frac{p - q}{2})}^{2} + b^{2}, \end{matrix}

ennélfogva

\begin{matrix} \sqrt[]{a^{2} - b^{2}} = e = \frac{p - q}{2} . \end{matrix}

Számítsuk ki az elvágott darab köbtartalmát:

\begin{matrix} k = \frac{a b π}{3} \cdot C R, de C R = p sin C D E, \end{matrix}

továbbá

\begin{matrix} q : 2 a = sin C D E : sin α, \end{matrix}

miből

\begin{matrix} sin C D E = \frac{q sin α}{2 a}, \end{matrix}

ennélfogva:

\begin{matrix} C R = \frac{p q sin α}{2 a}, \end{matrix}

tehát

\begin{matrix} k = \frac{a b π}{3} \cdot \frac{p q}{2 a} sin α = \frac{b p q π sin α}{6}, \end{matrix}

s így

b

értékét helyettesítve:

\begin{matrix} k = \frac{p q \sqrt[]{p q} π}{6} \cdot sin α sin \frac{α}{2} = \frac{π \cdot {(p q)}^{\frac{3}{2}} sin \frac{α}{2} cos \frac{α}{2}}{3} . \end{matrix}

Ezek után fektessünk

D

ponton át egy síkot, mely a kúpot úgy osztja, hogy a lemetszett kúp köbtartalma csonka kúpéhoz úgy aránylik, mint

m : n

.
Legyen

K

az egész kúp köbtartalma,

k

a lemetszett darabé, akkor

\begin{matrix} k = \frac{m}{m + n} K = \frac{m}{m + n} \frac{r^{2} π h}{3}, \end{matrix}

\begin{matrix} r = s \cdot sin \frac{α}{2}, h = s \cdot cos \frac{α}{2} \end{matrix}

s így

\begin{matrix} k = \frac{π {(p q)}^{\frac{3}{2}}}{3} sin^{2} \frac{α}{2} cos \frac{α}{2} = \frac{m}{m + n} \frac{π s^{3} sin^{2} \frac{α}{2} cos \frac{α}{2}}{3} \end{matrix}

\begin{matrix} {(p q)}^{\frac{3}{2}} = s^{3} \frac{m}{m + n}, p^{3} q^{3} = s^{6} {(\frac{m}{m + n})}^{2} \end{matrix}

\begin{matrix} p q = s^{2} \sqrt[3]{{(\frac{m}{m + n})}^{2}} és q = \frac{s^{2}}{p} \sqrt[3]{{(\frac{m}{m + n})}^{2}} . \end{matrix}

A feladat megoldhatására szükséges, hogy

\begin{matrix} s ≧ \frac{s^{2}}{p} \sqrt[3]{{(\frac{m}{m + n})}^{2}} \end{matrix}

legyen, vagyis

\begin{matrix} p ≧ s \sqrt[3]{{(\frac{m}{m + n})}^{2}}; \end{matrix}

m = n

, azaz

D

ponton át a kúp két egyenlő részre bontandó, akkor

\begin{matrix} q = \frac{s^{2}}{p} \sqrt[3]{\frac{1}{4}} . \end{matrix}

Ha a kúpot az alappal párhuzamos síkkal metsszük, azaz

p = q

, akkor

\begin{matrix} b = p sin \frac{α}{2}, e = 0, p = s \sqrt[3]{\frac{m}{m + n}} . \end{matrix}

Egy az alap kerületén fekvő ponton át síkok fektetendők, melyek a kúpot

μ

egyenlő részre osztják.
Ekkor

\begin{matrix} p = s, q = s \sqrt[3]{{(\frac{m}{m + n})}^{2}}, m + n = μ, m = 1, \end{matrix}

\begin{matrix} q_{1} = s \sqrt[3]{\frac{1}{μ^{2}}}, q_{2} = s \sqrt[3]{\frac{4}{μ^{2}}}, q_{3} = s \sqrt[3]{\frac{9}{μ^{2}}}, ... q_{μ - 1} = s \sqrt[3]{\frac{{(μ - 1)}^{2}}{μ^{2}}} . \end{matrix}

A kúp az alappal

φ

szöget bezáró sík által metszendő úgy, hogy a részek köbtartalmainak aránya legyen

m : n

.
Ekkor

\begin{matrix} C D E = 90^{\circ} (φ + \frac{α}{2}), C E D = 90^{\circ} (φ - \frac{α}{2}), \end{matrix}

továbbá:

\begin{matrix} p : q = cos (φ - \frac{α}{2}) : cos (φ + \frac{α}{2}), \end{matrix}

miből

\begin{matrix} q = \frac{p \cdot cos (φ + \frac{α}{2})}{cos (φ - \frac{α}{2})} \end{matrix}

és

\begin{matrix} p q = s^{2} \sqrt[3]{{(\frac{m}{m + n})}^{2}}, \end{matrix}

vagy

\begin{matrix} \frac{p^{2} cos (φ + \frac{α}{2})}{cos (φ - \frac{α}{2})} = s^{2} \sqrt[2]{{(\frac{m}{m + n})}^{2}} \end{matrix}

és

\begin{matrix} p = s \sqrt[]{\frac{cos (φ - \frac{α}{2})}{cos (φ + \frac{α}{2})}} \sqrt[3]{\frac{m}{m + n}} . \end{matrix}