Kezdőlap


Cím:	Vázlatok a mathematika történetéből 6. (Geminus, Serenus)
Szerző(k):	Baumgartner Alajos
Füzet:	1902/március, 173 - 175. oldal	PDF \| MathML
Témakör(ök):	Egyéb írások

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Geminus.

(Kr. e. I. század.)

Geminus valószínűleg Rhodoshan élt, talán ott is született. Életéről semmi adat nincsen és az az egy adat is, melyből tevékenységének idejét akarták kiszámítani, elég nagy zavart okozott. Írt ugyanis egy csillagászati művet (Ei

ρ α γ ω γ η

ε

ζ

τ α

φ α

ν

μ ε ν α

), melynek egyik helyén azt mondja: "A görögök az egyiptomiakra és Eudoxusra támaszkodva, azt veszik fel, hogy Isis ünnepe a legrövidebb nappal esik össze. Így volt ez egy alkalommal

120

évvel ezelőtt, de az eltérés minden négy évben egy nappal növekedik és ma már egy hónapot tesz ki".
A XVII. század egy jeles tudósa, Denis Petau (Petavius) franczia jezsuita abból indult ki, hogy Isis ünnepe Osiris megtalálásának emlékezete volt és mint ilyen a Kr. e. 197. év legrövidebb napjára esett. Ennélfogva Geminus Kr. e. 77 évvel írta művét.
A XVII. század alkonyán egy másik tudós, Bonjour egy római hagyományos adatot használt fel, mely szerint Isis ünnepe a Kr.-e. 257. év legrövidebb napján volt. Ez adat szerint tehát Geminus csillagászati művének kelete a Kr. e. 137. év.
A kérdést újabb időben Cantor döntötte el meggyőző bizonyítékokkal és a Kr. e. 77. évet jelentette ki helyes adatnak.
Geminus csillagászati művéből elegendő e helyen csak annyit megemlíteni, hogy magában foglalja Hipparchos elméletét a Napról (IX. évf. 54. lap), továbbá azt a feltevését, hogy az álló csillagok különböző távolságokban vannak tőlünk.
Írt Geminus még egy mathematikai művet is, mely azonban elveszett és melynek czíme és tartalma is majdnem ismeretlen. Pappus (Kr. u. III. századbeli író) egyik adata szerint a mű czíme ilyesféle lehetett: A mathematika elrendezéséről. Proklus (Kr. u. V. századbeli mathematikus) kommentárjából pedig azt olvassuk ki, hogy Geminus művében nevek és egyes történeti adatok fordultak elő, a nélkül azonban, hogy e mű ezért igazi mathematika-történeti munka lett volna, mint azt régebben hitték. Úgy látszik különben, hogy Geminus inkább filozófiai író volt, mert szívesebben foglalkozik geometriai magyarázatokkal, alapelvekkel és tételekkel, semmint mathematikai problémákkal. Erre és stílusára vonatkozólag álljon itt példának az a felfedezése, melyet Proklus őrzött meg: "A testekre szerkesztett vonalak közül némelyek részeikben egyenlők és hasonlók, mint a henger csavarvonalai; mások ellenben nem azok, mint az összes többi vonal. Kitetszik tehát e különbségekből, hogy csak három vonal van, melyek összes részeikben egyenlők és hasonlók: az egyenes vonal, a kör és a henger csavarvonala; ezek közül kettő a síkban fekszik és egyszerű, a harmadik azonban vegyes és testen van....... Ha ilyen, minden részében egyenlő és hasonló, vonalhoz egy külső pontból két egyenest húzunk, melyek vele egyenlő szögeket zárnak be, e két egyenes egyenlő hosszú."

Serenus.

(Kr. u. I. század.)

Serenus a Lesbos szigetén fekvő Antissa városában élt; egyéb adatunk nincs róla. Életének ideje sem ismeretes; Cantor csak úgy hozzávetőleg helyezi el a Kr. sz. u. I. századba.
Két értekezése maradt azonban reánk. ,,A kúp metszése" a jelentéktelenebb irat czíme. Annyiban érdemes róla megemlékezni, mert benne Serenus azokra a metszésekre is figyelmeztet, melyeket a kúp csúcsán átmenő síkok alkotnak. E metszési háromszögeket semmiféle elődje még nem vette figyelembe. Serenus továbbá e háromszögek maximális területével foglalkozik.
,,A henger metszése" czímű iratában már érdekesebb kérdésekkel foglalkozik Serenus. Az egyik feladat ez: adott kúphoz oly henger (és megfordítva: adott hengerhez oly kúp) keresendő, hogy ugyanaz a sík hasonló ellipsiseket messen ki mind a két testen. Két tétele a henger és kúp érintési viszonyairól szól.
Végre legérdekesebb az a tétele, mely (mai elnevezéseinkkel) harmonikus metszésekről szól.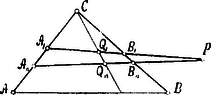

Serenus tétele ez: ha az

A B C

háromszöget (1. ábra) metsző és egy külső

P

ponton keresztülmenő egyenesen oly pontot:

Q_{1}

-et határozunk meg, hogy:

\begin{matrix} P A_{1} : P B_{1} = Q_{1} A_{1} : Q_{1} B_{1}, \end{matrix}

akkor a

C Q_{1}

egyenes a

P

pontból kiinduló bármelyik szelőnek részei között ezt az aránylatot állapítja meg:

\begin{matrix} P A_{n} : P B_{n} = Q_{n} A_{n} : Q_{n} B_{n} . \end{matrix}