|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. A projektív geometria egy érdekes tételéről, a Desargues-féle tételről óhajtok e helyen néhány szóval megemlékezni. E tétel, melyet egyrészt geometriai tartalma, másrészt czélszerű alkalmazásai tesznek egyaránt érdekessé és nevezetessé, a következő:
Két perspektiv fekvésű háromszög megfelelő oldalainak metszéspontjai egy egyenesen fekszenek.
Perspektívnek két háromszöget, egyáltalában két idomot, akkor mondunk, ha megfelelő csúcsaiknak összekötő egyenesei egy pontban metszik egymást. Az idézett tétel legegyszerűbben bizonyítható be a projektív geometria elveivel. Bonyolultabb az analytikai bizonyítás és a planimetriai. (K. M. L. IV. évf.) E helyen legczélszerűbbnek a következő bizonyítást tartjuk; egyrészt, mert a tételnek térben való fennállását is egyidejűleg igazolja, másrészt, mert mindjárt átvezet e tétel egy alkalmazására.
Messünk egy tetszőleges háromoldalú testszögletet (1. ábra), melynek élei , két tetszőleges és síkkal, és legyen a két sík metszésvonala . A keletkezett két metszési idom természetesen háromszög: és , melyek helyzetüknél fogva perspektívek.
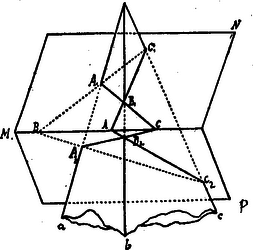 1. ábra
A és egyenesek mindketten ugyanazon síkban fekszenek és így egymást okvetlenül egy pontban metszik. De másrészt az , pedig az síkon fekszik és így a két egyenes közös pontja , csak a két sík közös egyenesén -en feküdhetik.
Ugyanígy mutatható ki, hogy a és egyenesek metszéspontja és a és egyenesek metszéspontja szintén egyenesen fekszik s ezzel a tétel a térben igazolva van.
Minthogy minden helyzet geometriai tétel, mely a térben érvényes, helyes a síkban is, mert a térben fennálló helyzeti vonatkozások vetítés által nem változnak, e tétel természetesen érvényes a síkban is. A háromszögekre kimondott tétel érvényes tetszőleges perspektív fekvésű síksokszögekre; hiszen háromoldalú testszöglet helyett oldalút is metszhettünk volna síkokkal.
A tétel fennáll természetesen akkor is, ha a perspektivitás középpontja a végtelenben van, azaz, ha a testszögletből (gúlából) prizma lesz.
Valamely gúla (v. kúp) illetőleg prizma (v. henger) két tetszőleges síkmetszete között fennálló ezen viszonyt, geometriai rokonságát az ábrázoló mértan centrális collineatió, illetőleg prizmák vagy hengerek esetében affinitás név alatt igen előnyösen alkalmazza gúlák (ill. kúpok) és prizmák (ill. hengerek)l síkmetszeteinek és e síkmetszetek valódi alakjának meghatározására. Ennek fejtegetésébe azonban olvasóink nagy részére való tekintettel mélyebbre hatolni nem kívánunk, hanem áttérünk az alkalmazását tekintve nem kevésbé fontos megfordítására a tételnek, mely így fogalmazható:
Ha két háromszög megfelelő oldalainak metszéspontjai egy egyenesen fekszenek, akkor a megfelelő csúcsokat összekötő egyenesek egy ponton mennek át.
E tételt külön bizonyítanunk nem is kell, a mennyiben a helyzet geometriai tételek között fennálló dualitás elve alapján van képezve az előbbiből.
E tétel néhány alkalmazását mutatják következő feladatok.
Két egyenesnek a rajzlapból kieső metszéspontjába rajzoljunk csak vonalzóval adott pontból egyenest.
A megoldás tételünk felhasználásával így történhetik:
A megadott pontból (2. ábra) két tetszőleges egyenest rajzolunk és ezeknek a megadott egyenesekkel való ill. metszéspontjait összekötjük.
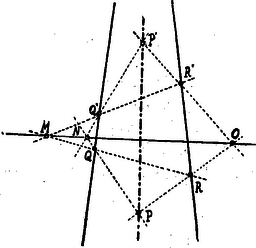 2. ábra
A -et tetszőleges egyenessel metszve, az így nyert metszéspontok bármelyikéből pl. -ből tetszőleges egyenest rajzolok, mely a két adottat ill. pontokban metszi. Az és egyenesek metszéspontját -vel összekötve kapcsoljuk a keresett egyenest.
Tökéletesen ezt az eljárást alkalmazzuk a következő feladatnál:
Adva két párhuzamos egyenes; rajzoljunk adott pontból csupán vonalzóval az adott egyenesekkel párhuzamosat.
Az eljárás ez esetben is teljesen azonos az előbbi esetben alkalmazottal, a mint az a 3. ábrából is kitűnik.
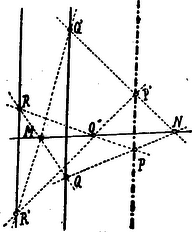 3. ábra
Az eljárás az, hogy e feladatot az előbbire visszavezetjük oly módon, hogy előbb oly pontot szerkesztünk, mely szintén rajta van a keresett egyenesen, de a rajzlapon belül esik. A (4. ábra) ugyanis oly háromszögnek tekinthető, melynek egyik csúcsa a végtelenben van.
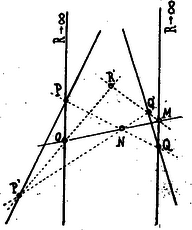 4. ábra
Ezt messük most tetszőleges egyenessel és szerkesszünk az előbbi szerint vele perspektív fekvésű háromszöget, melynek csúcsán megy majd át a keresett párhuzamos, a mivel ez az eset az előbbire van visszavezetve.
Gérard Desargues 1594‐1662. |
 PDF | MathML
PDF | MathML