| Cím: | Adva van két kör: keressünk olyan harmadikat, mely az adottakat érintse | ||
| Szerző(k): | Szirtes Ignácz | ||
| Füzet: | 1900/szeptember, 9 - 13. oldal |  PDF | MathML PDF | MathML |
|
| Témakör(ök): | Szakmai cikkek | ||
|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. Eme érintési föladat határozatlan, azaz végtelen sok oly kör van, melyek az adottakat érintik. Mindeme körök középpontjainak elhelyezkedésénél kell, hogy bizonyos szabályszerűség létezzék. Keressük e középpontok mértani helyét. 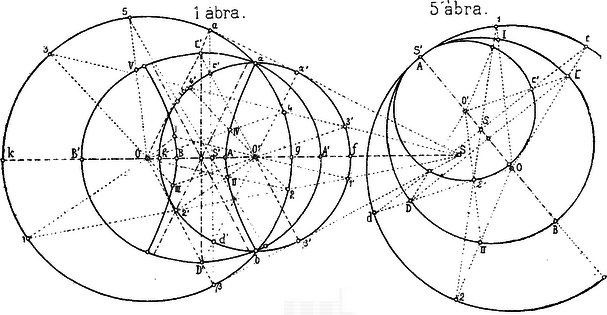 Vizsgáljuk a föltüntetett két mértani hely egymáshoz való viszonyát, tulajdonságait és jellemző részeit. Az ábra egyszerű megtekintéséből következik, hogy De
Az (1) alatt levő egyenlet azt jelenti, hogy mindazok a pontok, melyeket az adott körök külső hasonlósági pontjának segítségével állíthatunk elő, ama szerkesztés útján, mint a hogy az pontot nyertük, oly szabályszerűségnek hódolnak, hogy a két adott kör középpontjaitól mért távolságaiknak különbsége mindíg egy és ugyanazt az állandó mennyiséget adja. A (2) alatt levő egyenletnek meg az a jelentősége, hogy a belső hasonlósági pont segítségével szerkesztett minden pont ‐ mint a milyen az pont ‐ távolságainak összege az adott körök középpontjaitól egy állandó mennyiséggel egyenlő. E szerint az első mértani hely, melynek egyik pontja , hyperbola, melynek és a gyújtó pontjai és valós tengelye . A másik mértani hely pedig, melynek egyik pontja , oly ellipsis, melynek gyújtópontjai és és nagy tengelye . Vagyis e két mértani hely confocalis kúpszeletek. E kúpszeletek csúcspontjait még így is nyerhetjük: minthogy a hyperbola valós, illetőleg az ellipsis nagy tengelye a gyújtópontokat tartalmazza, azért a és , illetőleg és távolságok felezése által a hyperbola, illetőleg ellipsis csúcspontjait nyerjük ‐ és ‐. Az ellipsis kis tengelye végső pontjainak ‐ , ‐ szerkesztésénél vegyük az ponton áthaladó hasonló irányú segédegyenest szemügyre. A hyperbola assymptotáinak szerkesztésénél gondoljuk meg, hogy az adott köröknek a külső hasonlósági ponton áthaladó külső érintői oly egymással párhuzamos és egyenespárakra vezetnek, melyeknek a végtelenben levő metszéspontjai is az illető mértani helyen feküsznek. Vagyis: a hyperbola assymptotáit az egyenespárakkal párhuzamosan meghúzhatjuk a kúpszelet középpontján át. Megjegyezzük még, hogy ama körök középpontjai, melyek az adottak mindegyikét belülről érintik, az hyperbola ágon fekszenek ; az érintési pontok az és köríveken vannak. Az és pontokon túl az adott körök közös terén kívül levő pontjai e hyperbola ágnak a végtelenig oly körök középpontjai, melyek az adottakat az és köríveken, de kívülről érintik. A hyperbola másik ága oly körök középpontjainak mértani helye, melyek az adottakat az és íveken, de kívülröl, érintik. Ama körök, melyeknek középpontjai az ellipsisen vannak, mint már említettük, az adottak egyikét kívülről, másikát belülről érintik. A mértani helyek a köröknek és közös pontjain is átmennek. Az szöget felező egyenes a hyperbolának érintője ; mig a szöget felező egyenes ugyane pontban az ellipsist érinti. Következőleg: ha két confocalis kúpszelet közös pontokkal bír (metszés esetében az egyik ellipsis, a másik hyperbola), akkor egymást derékszög alatt metszik. (b) 2. ábra. Az adott körök nem metszik egymást és egymáson kivül vannak. 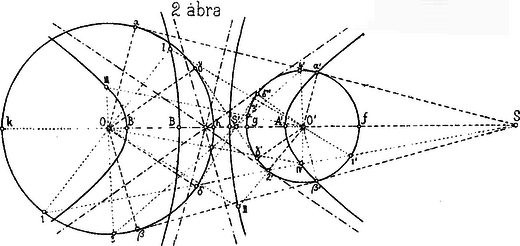 Ez esetben a két mértani hely mindegyike hyperbola. A közös gyújtópontokra, assymptotákra és valós tengelyekre tett megjegyzések itt is, valamint a még következö eseteknél is érvényesek. Itt valamennyi kör az adottakat kivülről érinti, de a viszonyok másképpen alakulnak, mint az (a) esetben. Ugyanis az külső hasonlósági pontnak megfelelő hyperbola assymptotái párhuzamosak és -hoz, a valós tengely. Az ág oly körök középpontjait (egy ilyen pont az középpont) foglalja magában, melyek az adottakat egészen körülfogják és az érintési pontok az és köríveken vannak. E hyperbola másik ága pedig mértani helye ama körök középpontjainak, melyek az adott körök egyikét sem fogják körül és őket az és köríveken érintik (egy ilyen pont a II. középpont). Az belső hasonlósági pontnak megfelelő hyperbola assymptotái párhuzamosak az és -hoz ( és az adott körök közös belső érintőinek érintéspontjai), valós tengelye . ágban találjuk ama körök középpontjait (egy ilyen a . pont), melyek a közelebbi középpontú kört körülfogják, míg a távolabbi középpontú kört nem fogják körül; az érintési pontok e szerint a és , köríveken vannak. E hyperbola másik ága pedig ama körök középpontjainak képezi mértani helyét (pl. IV. pont), melyek a közelebbi kört körülfogják és a kört nem fogják körül; az érintési pontok a és köríveken vannak. (c) 3. ábra. Az adott körök nem metszik egymást (és egyik kör a másikon belül van. Ebben az esetben egyik hasonlósági pontból sem lehet a körökhöz érintőket szerkeszteni, tehát mind a két mértani hely ellipsis. Az hasonlósági pont segítségével előállítható ellipsis tengelyei és . Ama körök, melyeknek középpontjait (ilyen az pont) ez az ellipsis tartalmazza, az középpontú kört a homorú, az középpontút pedig a domború oldalon érintik. Az érintési viszonyok ugyanilyenek a másik körrendszernél is. 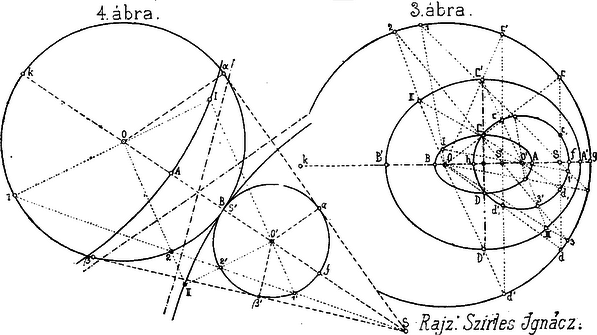 (d) 4. ábra. Az adott körök úgy érintkeznek, hogy egyik kör a másikon kívül marad. A külső hasonlósági pontnak megfelelő hyperbola egyik csúcspontja a körök közös érintési pontja. Ama körök középpontjai, melyek az adottakat az és körívek pontjaiban érintik, a hyperbola ágban vannak, e körök az adottakat nem fogják körül. A hyperbola másik ágában pedig oly körök középpontjai vannak, melyek az adottakat körülfogják; az érintési pontok az és köríveken vannak. A másik mértani hely, az egyenes és a megfelelő körök az adottakat a közös pontban érintik. mert az és -ból kiinduló megfelelő sugarak ez esetben párhuzamosak egymással. (e) 5. ábra. Az adott körök érintkeznek és egyik a másikon belül marad.  Az hasonlósági pontnak megfelelő kúpszelet az AB és CD tengelyekkel bíró ellipsis. A másik mértani hely ismét az egyenes. |