Cím: Coordináta rendszerekről 2.: Coordináta rendszerek a síkban 1.
Szerző(k):  Dr. Horti Henrik 
Füzet: 1901/február, 153 - 161. oldal  PDF  |  MathML 
Témakör(ök): Szakmai cikkek

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. Coordinata rendszerek a síkban.

 
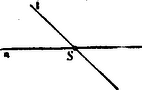
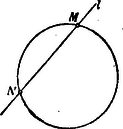
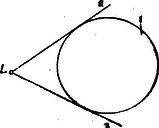
A)Parallel pontcoordináták.
 
1. A derékszögű rendszer. Ha a síkban két egymást derékszög alatt metsző XX1 és YY1 egyenes vonalnak a helyzetét ismerjük, akkor a két egyenes alapján biztos következtetést vonhatunk a sík bármely pontjának helyzetére.
A P pont helyzetét ugyanis meghatározzák a pontnak az egyenesektől mért PM és PN merőleges távolságai (1. ábra.).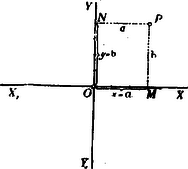
 

 

1. ábra
 

A síkban derékszög alatt rajzolt XX1 és YY1 egyenesek derékszögű (orthogonális) parallel-coordináta tengelyrendszert alkotnak.
A PN=OM=a távolság a P pont abscissája; a PM=ON=b, a pont ordinátája. Az XX1-vonal az abscissák, az YY1 az ordináták tengelye; O metszőpontjuk a rendszer kezdőpontja. Az abscissát röviden x, az ordinát y betűvel jelöljük.
Hogy a parallel-coordináta-rendszerben bizonyos pont helyzetének meghatározására csakugyan két adat kivántatik, könnyen beláthatjuk, ha megfontoljuk, hogy az x=a, vagyis OM távolság (2. ábra.) egymagában nemcsak egy, hanem a sík végtelen sok, t.i. az M ponton áthaladó és az ordináta tengellyel párhuzamos egyenes összes pontjainak közös abscissája.
 

 

2. ábra
 

Viszont, egymagában az y=b sem elegendő, mert ez közös ordinátája az N ponton áthaladó és az abscissa tengellyel párhuzamos helyzetű egyenes bármely pontjának (3. ábra.).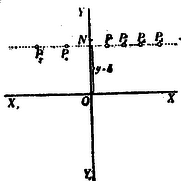
 

 

3. ábra
 

Ezért a sík egyetlen egy pontjának biztos megjelölésére az x=a-t és egyidejűleg y=b-t kell ismerni. Parallel rendszerben tehát két coordinata egy pontot határoz meg, és viszont a sík minden pontjához két coardinata tartozik.
Ha az a és a b távolságok adva vannak, akkor a pontot közvetlenül meg lehet szerkeszteni; ha azonban a-nak és b-nek csak mérőszámait ismerjük (pl. x=3,y=4) akkor még valamely mérőegységre van szükségünk, melyet a kezdőpontból kiindulva az x tengelyre a-szor és az y tengelyre b-szer fölrakunk. Csak ennek megtörténte után szerkeszthetjük meg azt a parallelogrammal, melynek egyik csúcsában a keresett P pontot nyerjük (1. ábra.). Ama körülményre való tekintettel, hogy az XX1 és YY1 tengelyek az egész síkot négy részre osztják, a P pont teljes (egyértelmű) meghatározására még az sem elegendő, ha két coordinátájának csak absolut értékét ismerjük. Minden kétség elkerülése végett tehát a coordinata tengelyek részeit (és velük együtt a coordinatákat) a kezdő ponttól számítva irány szerint előjellel különböztetjük meg. Hogy a pontot a sík melyik negyedében kell keresnünk, azt tehát coordinatáinak előjelei mutatják. (Lásd a 4. ábrát.)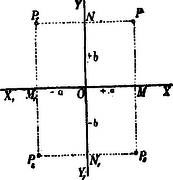
 

 

4. ábra
 

Általában azonban mondhatjuk, hogy az x=a és y=b két egyenlet algebrai módon fejezik ki a pont helyzetét a coordinata tengelyek között. A pont helyzetének megjelölésére azonban más algebrai relatiókat is találhatunk. Azok az algebrai egyenletek, melyek megoldásképpen az x=a és y=b alakú egyenleteket szolgáltatják, a pontnak algebrai representansai.
Így mondhatjuk, hogy két elsőfokú, két ismeretlent (a coordinátákat) tartalmazó egyenlet egy pontot határoz meg.
Mert, ha
{f(x,y)=ax+by+c=0φ(x,y)=a1x+b1y+c1=0
egyenletrendszert megoldjuk, akkor x=bc1-b1cab1-a1b és y=a1c-ac1ab1-a1b azaz x-re és y-ra nézve egy-egy értéket nyerünk, melyekből a pontot megszerkeszthetjük. Pl.
{2x+5y=193x-7y=-15
Megoldás:  x=2;y=3.

A belőlük megszerkesztett M pontot az 5. ábrában látjuk.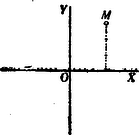
 

 

5. ábra
 

A geometriai hely. Egészen más a dolog, ha csak egy egyenletünk van. Egyetlen-egy két ismeretlent tartalmazó egyenlet már nem egy, vagy esetleg csak néhány pontot, hanem a pontoknak egész sorozatát képviseli. Valahányszor ugyanis az y=f(x) algebrai egyenletben x-nek bizonyos értéket adunk, mindannyiszor y-nak is bizonyos érték felel meg. Ezért mondhatjuk, hogy x-hez és y-hoz a különböző értékek egész rendszerei tartoznak. Ha ama értékekben sorban +∞-től -∞-ig haladunk, és x-nek és y-nak együvé tartozó értékeiből a megfelelő pontokat megszerkesztve képzeljük, akkor a pont geometriai helyét nyerjük; az eredmény vonal lesz.
A geometriai hely egyenes- vagy görbe-vonal lehet; hogy milyen lesz, az az egyenlettől függ (6. és 7. ábra.).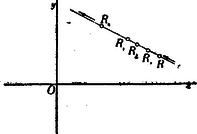
 

 

6. ábra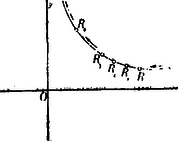
 

 

 

7. ábra
 
Vannak algebrai és transcendens egyenletek. Minden egyenlet geometriai helyet képvisel, azért vannak algebrai és transcendens vonalak. Csakis két ismeretlent tartalmazó algebrai egyenleteket tartván szem előtt, mondhatjuk, hogy a Descartes-féle pontcoordinatákban az elsőfokú egyenlet egyenes vonalat jelent és könnyű szerrel viszont kimutatható, hogy az egyenes vonalnak az egyenlete mindenkor elsőfokú.
Már a másodfokú és azon túl minden magasabb fokú egyenlet görbe vonalat képvisel. Nevezetesen, a másodfokú egyenlet másodrendű, a harmadfokú, harmadrendű stb. az n-edfokú n-edrendű sík görbét representál.
A sík-görbéket egyszerű görbületű görbéknek nevezzük, szemben a térbeli görbékkel, melyeket kettő-görbületűeknek mondunk. Habár szorosan véve nem tartozik e cikksorozat keretébe, mellékesen megjegyzem, hogy az egyszerű görbületű görbék rendszáma alatt ama pontok számát értjük, mely pontokban valamely egyenes vonal az illető görbét metszi.
Mivel az egyenes vonalat más egyenes csak egyetlenegy pontban metszheti, azért az egyenest elsőrendűnek mondjuk. A másodrendűeket (a kört, a kúpszeleteket), az egyenes két, a harmadrendűeket három, általában az n-edrendűeket n pontban metszi.
Vajon valósak- vagy képzetesek-e a metszőpontok és ha valósak, a véges térben feküsznek-e vagy a végtelenben, az a metsző egyenes helyzetétől és a görbe vonal természetétől függ. Érdekes, hogy, mint a metsző egyenesről, a sík úgynevezett végtelenben fekvő egyeneséről is szólhatunk.
Az Ax+By+C=0 elsőfokú egyenlet az egyenes egyenletének legáltalánosabb alakja. Benne A,B és C állandó mennyiségek és ezek határozzák meg az egyenes helyzetét a síkban (t.i. a coordinata tengelyek között). Az x és y pedig ama pontnak a coordinatái, mely pont az egyenest leírja. Más szóval az egyenes egyik pontjának változó coordinatái. Az egyenes egyenletének leggyakrabban használt alakjai: y+mx+n;xa+yb=0;xcosα+ysinα-p=0; ahol az állandóknak az egyenletek mindegyikében más-más jelentősége van.
Az xa+yb=1; alakú egyenletben a és b alatt azt a két metszéket értjük, melyeket az egyenes a tengelyeken meghatároz (9. ábra.).
Ha az Ax+By+C=0 általános alakú egyenletben C=0; akkor az Ax+By+C=0 egyenlet olyan egyenest képvisel, mely a rendszer kezdőpontján áthalad. Ebben az esetben az egyenest meghatározza az yx=-AB=tgα; ahol α alatt ama szöget értjük, melyet az egyenes az abscissák tengelyével alkot.
Ha A=0 akkor By+C=0. Ez olyan egyenesnek az egyenlete, mely az x tengellyel párhuzamos. Az x-től való merőleges távolságát y=-CB mutatja
Ha B=0; akkor Ax+C=0. Ez az y tengellyel párhuzamos egyenesnek az egyenlete. Belőle x=-CA, meghatározza az y-tól való távolságát.
Ha továbbá az Ax+By+C=0 egyenletet -C-vel elosztjuk, az egyenletet -ACx-BCy-1=0 alakra hozzuk, és ezt, az xa+yb=1 alakúval összehasonlítjuk, nyerjük: a=-CA és b=-CB. Ebből láthatjuk, hogy a (-CA) és (-CB) törtek értékei az egyenes vonal általános egyenletében ama metszékeket határozzák meg, melyeket az egyenes a tengelyekkel alkot.
Minél kisebbek a nevezők, annál nagyobbak a törtek értékei. Ha A=0 és B=0, akkor (C-nek változatlan értéke mellett) a két metszék végtelen nagy és az egyenlet olyan egyenest képvisel, melynek minden pontja a végtelenben van; más szóval az egyenlet végtelenben fekvő egyenest jelent.
A másodfokú egyenlet legáltalánosabb alakja:
ax2+2bxy+cy2+2dx+2ey+f=0.
Ez általános képviselője az összes másodrendű görbéknek. Hogy minő fajtájú, alakú és helyzetű másodrendű görbével van dolgunk, azt az egyenlet állandóiból tudhatjuk meg. Főleg attól függ, vajon vannak-e az egyenletben egyenlő és nulla értékű együtthatók és melyek azok.
A magasabb rendű algebrai síkgörbék egyenletei általában a másodrendűekéhez hasonló alakúak ugyan, de a fokszámra való tekintettel complikáltabb szerkezetűek.
2. Ferdeszögű (klinogonális) parallel coordinata-rendszer. Habár az egyszerűség és kényelem szempontjából az analytikai számításokban többnyire derékszögű coordinatákat alkalmazunk, azért használunk némelykor olyan rendszereket is, melyekben az ordinata tengely az abscissa tengelyt hegyes, illetőleg tompa szög alatt metszi (8. ábra.).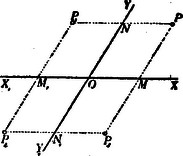
 

 

8. ábra
 

Azokat a rendszereket ferdeszögűeknek (klinogonálisoknak) nevezzük. Mint az orthogonalis, úgy a klinogonális rendszer is parallel-coordinata rendszer, és a kettő közül bizonyára a klinogonális az általánosabb jellegű.
A ferdeszögű rendszerben a P pont coordinatait nyerjük, ha a ponttól az abscissa, illetőleg ordinata tengelyhez párhuzamosokat húzunk. Természetes, hogy az előjelet itt is figyelembe vesszük, nemkülönben a számításokban tekintettel vagyunk a tengelyek alkotta szög nagyságára.
 
B)Vonalcoordináták.
 

Nemcsak a pontnak, hanem az egyenes vonalnak a helyzetét is a síkban két adat teljesen meghatározza. Meghatározzák ama a és b távolságok, melyeket az l egyenes a tengelyekből (az O ponttól számítva) lemetsz (9. ábra.).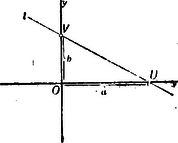
 

 

9. ábra
 

Jelöljük a-nak és b-nek negatív reciprok értékeit u-val és v-vel,(t.i-1a=u és -1b=v); akkor az u és a v értékeket az egyenes a vonal coordinatáinak, röviden vonalcoordinatáknak nevezzük.
Könnyen beláthatjuk, hogy valamely két ismeretlent tartalmazó elsőfokú egyenletnek nemcsak abban az esetben van geometriai jelentősége, ha a benne lévő ismeretleneket valamely pont változó coordinatáinak vesszük, hanem akkor is, ha ama ismeretleneket valamely egyenes vonal változó meghatározó adatainak (coordinatáinak) tekintjük.
Ha ugyanis valamely f(u,v)=0 alakú egyenletünk van, akkor u különböző értékeinek egész rendszeréhez ‐ az egyenlet kapcsán ‐ v különböző értékeinek egész rendszere is tartozik. Ha az u-nak tulajdonított értékekben rendre+∞-től -∞-ig haladunk, a v-ket meghatározzuk és az u-nak és v-nek együvé tartozó értékeiből a különböző egyeneseket rendre megszerkesztve képzeljük, akkor a vonalcoordinatákban ugyanazzal a joggal szólhatunk az egyenes vonal geometriai helyéről, a mellyel a pontcoordinatákban a pont geometriai helyét hangoztattuk. Közvetetlen egymásután következő (végtelen közel egymás mellett fekvőnek képzelt) 1,2,3,4... metsző helyzeteivel az egyenes valamely görbe vonalat beburkol, úgy hogy mindegyik egyenes érintője a görbének (10. és 11. ábra.).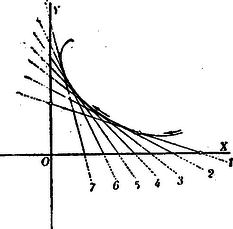
 

 

10. ábra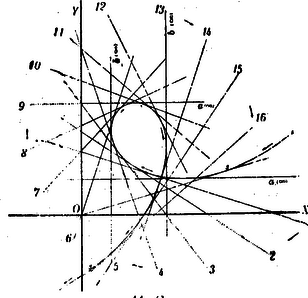
 
 

 

11. ábra
 

A görbe enveloppja az egyeneseknek. Ha az egyenes valamelyik helyzetében a coordinata tengelyek egyikével párhuzamos, akkor az illető tengelyen lévő metszéke természetesen végtelen nagy (11. ábra.).
Ebben az egyenletben ux+vy-1=0 az u és v vonalcoordinaták; x és y pontcoordinaták. Ennek az a magyarázata, hogy a pont, melynek coordinatáit x-szel és y-nal jelöltük, rajta van ama egyenesen, melynek coordinatáit u-val és v-vel jelöljük. Minthogy ebben az egyenletben tulajdonképpen négy változó mennyiséget látunk, azért az egyenletnek kettős értelme van. ‐ Nevezetesen, ha u és v adva van, akkor az egyenletben csak az x és y változó mennyiségek maradnak. Ha ebben az esetben x-nek különböző értékeihez az y-okat megszerkesztjük, akkor ‐ geometriailag fejezvén ki a dolgot ‐ az (x,y) pont leírja azt az egyenest, melynek u és v a coordinatái. (Ez tehát az egyenletnek az értelme pontcoordinatákban.) Ha ellenben x-t és y-t adottnak (pl. x=ξ és y=η), ellenben u-t és v-t változóknak képzeljük, akkor az egyenlet ilyen alakot ölt ξu+ηv-1=0, és geometriai interpretálásban azt jelenti, hogy mind ama egyeneseknek egyenlete, melyek a ξ,η ponton áthaladnak. Más szóval az u és v coordinatákkal bíró egyenesek, a (ξ,η) pontot beburkolják. (Ez az egyenletnek az értelme vonalcoordinatákban.)
A ξu+ηv-1=0 egyenlet tehát vonalcoordinatákban mindenkor a pontnak az egyenlete
Ha a ξu+ηv-1=0 egyenletben η=0; akkor a ξη-1=0, az abscissa tengely ama pontjának az egyenlete, melynek távolságát a rendszer kezdüpontjától a ξ érték mutatja.
Ha ξ=0, akkor ηv-1=0, az ordinata tengely ama pontjának az egyenlete, mely a kezdőponttól η távolságban van. Ha az egyenletből az állandó tag hiányzik, az egyenlet ξu+ηv=0 alakú. Belőle vu=-ξη. Ez jelenti mind ama egyeneseknek közös metsző pontját, mely egyenesek coordinatái állandó értékű viszonyt alkotnak. Tekintettel arra, hogy olyan helyzetű egyenesek okvetetlenül párhuzamosak, az egyenlet párhuzamos egyenesek metsző pontjának az egyenlete. Párhuzamos egyeneseknek a metsző pontja a végtelenben van, azért a ξu+ηv=0 a végtelenben fekvő pontnak az egyenlete. Irányát a -ξη viszony mutatja.
Fölötte tanulságos az a körülmény, hogy pontcoordinatákban a pont, vonalcoordinatákban pedig az egyenes vonal ama alapelem, melyből a sík összes (egyenes- és görbe vonalú) idomai alakíthatók. A planimetriában tehát a pont és az egyenes egyenlő jogosultságú ‐ úgynevezett duális ‐ elemek. A vonalcoordinaták elmélete a dualitás elvén alapszik.
 
*
 
Másod- és magasabb fokú egyenletek vonalcoordinatákban is görbe vonalú geometriai helyeket (görbéket) képviselnek.
Vonalcoordinatákban a görbéket osztályszámaik szerint különböztetjük meg. A görbe vonal osztályszáma megegyezik (vonalcoordinatákra vonatkoztatott) egyenletének fokszámával.
A görbe vonal osztálya alatt azt a számot értjük, mely megmutatja, hogy a görbe vonal síkjának egyik pontjából hány érintőt lehet a görbéhez húzni.
Vajon az érintők valósak- vagy képzetesek-e és ha valósak, érintő pontjaik a véges térben vagy a végtelenben vannak-e, mind az, az érintő helyzetétől és a görbe vonal természetétől függ.
 
*
 

Vonalcoordinatákban a másodfokú egyenletnek általános alakja
au2+2βuv+γv2+2δu+2εv+ϰ=0.
Ez képviselője minden másodosztályú görbének. Hogy minő fajtájút, alakút és helyzetűt jelent, az, az egyenlet együtthatóitól (α,β,γ,... állandóitól) és egyéb körülményektől függ.
A magasabb osztályú algebrai síkgörbék egyenletei a másodrendűekéhez általában hasonló, de a magasabb fokszámra való tekintettel bonyolódottabb szerkezetűek.
 
*
 

Hogy a pont- és vonalcoordinaták között a dualitás elvén nyugvó szoros kapcsolat van, közvetlenül láthatjuk, ha a talált nehány eredményt a rend-és osztályszám szempontjából párhuzamba állítjuk.

 Pontcoordinatákban: Vonalcoordinatakban:  1. az  ux+vy-1=0  elsőfokú egyenlet  egyenes vonalat  1. az  xu+yv-1=0  elsőfokú egyenlet  pontot  jelent,  jelent, ha benne  x  és  y  változó;  u  és  v  állandó  ha benne  u  és  v  változó;  x  és  y  állandó mennyiségek.  mennyiségek. Az egyenes  első-rendű,  mert valamely  A pont  első-osztályú, mert valamely pontból egy  egyenest egy másik egyenessel csak egyetlen egy pontbanmásik ponthoz csak egyetlen egy egyenes vonalat    metszhetünkhúzhatunk.  Más szóval, mert két egyenesnek csak egyetlenMás szóval, mert két pontot csak egyetlen egy  egy metsző pontja van (12. ábra.).egyenes vonallal lehet összekötni (13. ábra.).

 
12. ábra
 
13. ábra

Tehát minden lineáris egyenlet pontcoordinatákhan egyenesnek, és vonalcoordinatákban pontnak az egyenlete.

  2. Az  ax2+2bxy+...+f=0  másodfokú egyenlet2. Az  au2+2βuv+...+x=0  másodfokú egyenlet  a  másodrendű görbéknek (körnek,  a  másodosztályú görbéknek (körnek,  kúpszeletnek) általános egyenlete. Az egyenes  kúpszeletnek) általános egyenlete.  a másodrendű görbét két pontban metszi  Egy pontból a másodrendű görbéhez két érintőt(14. ábra.).  lehet húzni (15. ábra.)

 
14. ábra
 
15. ábra