Cím: Vázlatok a mathematika történetéből 5. (Nikomedes)
Szerző(k):  Baumgartner Alajos 
Füzet: 1901/január, 129 - 133. oldal  PDF  |  MathML 
Témakör(ök): Egyéb írások

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

N i k o m e d e s.
 
(Kr. e. II. század.)
 
A Kr. e. III. század három óriásának működése után nem igen lehetett szó újabb eredményekről, további fejlődésről a mathematika terén. Euklides, Archimedes és Apollonius a lehető legmagasabb fokra emelték tudományukat bámulatos lángelméjükkel; kisebb tehetségek csakis az esetleg továbbra is megoldás nélkül maradt kérdésekkel foglalkozhattak vagy olyanokkal, melyeket amazok vetettek fel. Azért is ne csodálkozzunk, a mikor e nagy eredmények után ismét csak a delosi problema, a triszekczió, esetleg egy-egy körmérési feladat lép fel és a Kr. e. II. század mathematikusai összes munkásságukat csak ily kérdésben fejtik ki. Hiszen mi magunk, kik pedig mathematikai módszerben nevelve, néhány évi tanulás után megismerhetjük mindazt, a mit e nagy elmék 2000 évvel ezelőtt tudtak, nemcsak bámulva csodáljuk ez eredményeket, hanem egyszerűen érthetetlen rejtélynek tartjuk azt a körülményt, hogy ők tulajdonképpen rendszeres mathematikai iskolázottság híján annyi tudomány birtokába tudtak jutni és e tudományhoz még módszert is adni. Szinte természetesnek tűnik fel, hogy ekkora haladás után bizonyos stagnálás álljon be: a haladás oly rohamos volt, hogy az elmék nem is voltak eléggé érettek és elkészültek arra, hogy ez óriási anyaggal megküzdjenek. Nem csoda tehát, hogy a nagy mathematikusokat közvetlenül követők nem bírtak arra a magaslatra fellépni, melyen azok voltak és nem gyarapították a tudományokat nagyszabású munkálatokkal, sem módszert nem dolgoztak ki, hanem megelégedtek az előbb említett, szinte már konvenczionális kérdésekkel.
Elsőnek Nikomedest említjük meg azok közül, kiknek neve e problémákhoz fűződik. Személyéről egyebet nem tudunk, mint azt, hogy Kr. e. 200 körül szerkeszthette meg azt a görbe vonalat, mellyel a következőkben részletesebben foglalkozunk.
 

 

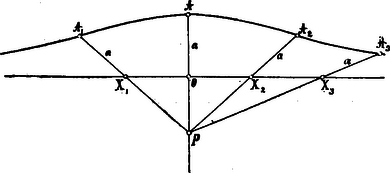
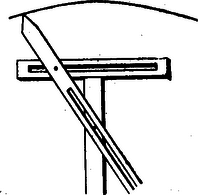
E görbe neve: kagylóvonal (conchois) és úgy keletkezik, hogy egy egyenesnek (1. ábra) állandó P pontjából sugarakat húzunk az ezen egyenesre merőleges OX egyenesnek egyes pontjaihoz: O,X1,X2,X3,... és e pontokból a sugarakra állandó a távolságot rakunk fel A,A1,A2,A3,... felé, úgy hogy:
a=OA=X1A1=X2A2=X3A3=...
Nikomedes maga ezt a P pontot pólusnak (πóλoσ) nevezte, a görbét pedig egy eszköz segélyével rajzolta meg. Ez eszköz szerkezetét a mellékelt ábra teljesen megérteti: bővebb magyarázatra nincs szükség.
 

 
Nikomedes azt mutatta ki e vonalról, hogy az mindinkább közeledik az állandó egyeneshez és hogy minden egyenes vonal, mely az állandó egyenes és a kagylóvonal között fekszik, ez utóbbit metszi, végre pedig felhasználta a görbét a delosi probléma megoldására, a miben páratlan mathematikai éleslátást tanúsított. Nikomedes eredeti szerkesztése a következő: legyen a két egyenes a és b, melyeknek kétszeresei közé két középarányos: x és y ékelendő, úgy hogy a következő aránylat legyen:
2a:x=x:y=y:2b.
Szerkesszünk oly derékszögű háromszöget, melynek egyik befogója: OA=a és átfogója: OB=b (1. ábra).
 

 

Vigyünk fel továbbá a befogó meghosszabbítására O ponttól jobbra és balra OC és OD távolságokat, melyeknek mindegyike 2a-val egyenlő. Húzzuk meg a BD egyenest és ezzel a C ponton keresztül CX párhuzamost. Mármost legyen ez a CX egyenes oly kagylóvonalnak állandó egyenese, melynek polusa a B pont és melynek állandó távolsága b legyen. E kagylóvonal a DOC egyenest E pontban metszi; kössük össze az E pontot B-vel egyenes vonallal, mely a CX egyenest F pontban metszi. Mivel DB és CF párhuzamosak, a következő aránylat áll fönn:
DE:CE=BE:FE;
ha CE-t y-nal és BF-et x-szel jelöljük, így írhatjuk az aránylatot:
(4a+y):y=(x+b):b.
Vonjuk ki az utótagokat az előtagokból, lesz :
4a:y=x:b,
miből:
xy=4ab;
ezt az egyenletet ismét más aránylatban fejezhetjük ki :
2a:x=y:2b.

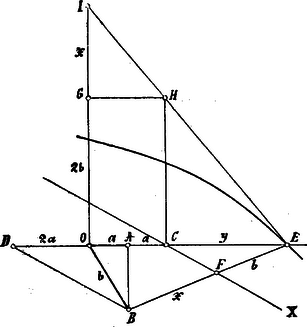
Most még csak az x és y közötti arányt kell megtalálnunk. E végből vegyük tekintetbe, hogy az AB egyenes az OAB és EAB derékszögű háromszögek közös befogója és mint ilyen, négyzete a Pythagoras tétele által kifejezhető:
OB2¯-OA2¯=EB2¯-EA2¯;
az egyszerűbb jelzéseket behelyettesítve:
b2-a2=(x+b)2-(a+y)2;
miből:
x(x+2b)=y(y+2a);
tehát:
x:y=(y+2a):(x+2b).

Ezt az utóbbi: (y+2a):(x+2b) arányt azonban még máshonnan is meg kell határoznunk. Szerkesszünk az OC=2a oldalra OCHG téglalapot, melyben OG=2b és kössük össze az E pontot a H ponttal, úgy hogy ez az egyenes meghosszabbítva I pontban messe az OG oldal meghosszabbítását. Mivel IGH és HCE hasonlók egymáshoz, azért:
GH:GI=CE:CH,
vagyis:
2a:GI=y:2b
Mert azonban már egy
2a:x=y:2b
aránylatunk volt, azért tehát GI=x. Végre pedig IOE és HCE háromszögek is hasonlók; e miatt:
OR:OI=CE:CH,
vagyis:
(y+2a):(x+2b)=y:2b.
Mivel pedig már egy
x:y=(y+2a):(x+2b)
aránylatunk volt, ez a most nyerttel egybevetve, lesz:
x:y=y:2b
s így végre:
2a:x=x:y=y:2b.
Nikomedes a kagylóvonalat valamely szögnek megharmadozására is igen ügyesen felhasználta.
 

 

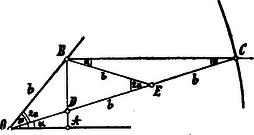
E czélból a φ szög egyik szárára AB merőlegest állítunk (l. ábra); ezt a vonalat felhasználjuk oly kagylóvonal állandó egyeneséül, melynek polusa az O pont és melynek állandó távolsága: az OB=b átfogónak a kétszerese; a kagylóvonal C pontban metszi a B ponton keresztül, az OA-val vont párhuzamost; kössük össze még a C pontot O-val, akkor a COA∢=α máris a φ szögnek harmadrésze. Ezt könnyen bebizonyíthatjuk: legyen az OC metszési pontja az AB-vel: D, akkor a feltétel szerint CD=2b; ha pedig e CD egyenes középpontját E-vel jelöljük, akkor azt látjuk, hogy a BCE és OBE háromszögek egyenlőszárúak; a BCE háromszögben a két egyenlő szög: BCE∢=CBE∢=α; mivel pedig a BED∢ a BEC∢ mellékszöge, azért az OBE háromszögben a két egyenlő szög: BED∢=BOD∢=2a. Végre pedig BCE∢=AOD∢=α, mint belváltószögek s így csakugyan φ=3α.