Cím: Pascal tétele egyenes pár esetében
Szerző(k):  Kürschák József 
Füzet: 1900/január, 93 - 96. oldal  PDF  |  MathML 
Témakör(ök): Szakmai cikkek

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

1. Pascal* tétele a kúpszeletbe írt hatszögre vonatkozik, de mi arra az esetre szorítkozunk, mikor a kúpszelet két egyenesből áll. Ekkor a tétel így szól:
Legyen adva egy sík két e és e' egyenesén három-három pont

A,B,Cill.A',B',C',
de úgy, hogy egyikök sem essék a két egyenes metszéspontjába. Ekkor az AB'CA'BC' hatszögnek egymással átellenes
a=B'Césa'=BC'
b'=CA'ésb=C'A
c=A'Bésc'=AB'
oldalainak P,Q és R metszéspontjai egy egyenesen vannak. (1. ábra.)
 

 

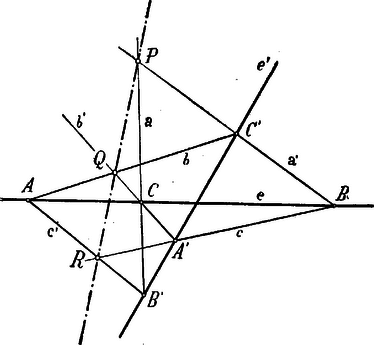1. ábra
 

2. Hogy a tétel az adott pontok bármely helyzetére alkalmazható legyen, két párhuzamos egyenesnek is tulajdonítunk közös pontot. Ezt a pontot e két egyenes végtelen pontjának mondjuk. Továbbá a sík végtelen pontjainak geometriai helyét egyenesnek tekintjük. Ezt az egyenest az illető sík és minden vele párhuzamos sík végtelen egyenesének mondjuk. A tér összes végtelen pontjainak geometriai helyét síknak tekintjük, és ezt a végtelen síknak mondjuk. 3. Bizonyítsuk be Pascal tételét először arra az esetre, midőn e' a síknak végtelen egyenese. (2. ábra.)
 

 

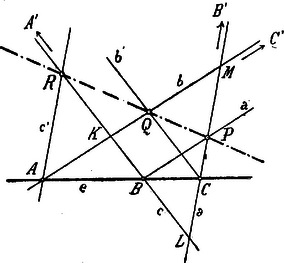2. ábra
 

Ekkor A',B' és C' a végtelenben vannak és úgy adandók meg, hogy (nyilakkal) kijelöljük, mily irányú egyeneseken vannak a végtelenben. Az a,b,c egyeneseket úgy rajzoljuk meg, hogy e-nek adott C,A,B pontjain keresztül a kijelölt irányokban vonjuk meg. Az a',b',c' egyeneseket pedig úgy kapjuk meg, hogy B,C ill. A-n keresztül b,c ill. a-val párhuzamosokat húzunk.
Ha az a,b és c egyenesek által meghatározott háromszög csúcsait K,L és M-mel jelöljük, akkor Menelaos tétele (K.M.Lapok IV. évf. 148. l.) szerint
CLCM⋅AMAK⋅BKBL=1.
Ámde b' és c,c' és a, végre a' és b párhuzamossága miatt
CL:CM=QK:QM
AM:AK=RL:RK
BK:BL=PM:PL.

Ennélfogva
RLRK⋅QKQM⋅PMPL=1,
tehát Menelaos tételének megfordítása szerint P,Q és R valóban egy egyenesen vannak.
4. Legyen most e és e' a síknak két véges egyenese. Ezt az esetet vetíttéssel, még pedig ú. n. czentrális projekczióval, visszavezetjük az előbbire.
E végből vegyünk fel a síkon kívül, melyben a vizsgálandó ábra van, egy másik síkot, a képsíkot, továbbá a térben egy S pontot, a czentrumot (az utóbbit úgy, hogy sem a vetítendő ábrának síkjába, se a képsíkba ne essék). A vetítendő ábra egy tetszőleges pontjának, pl. A-nak vetületét vagy képét úgy kapjuk, hogy e pontot egyenes vonallal összekötjük a czentrummal, és az így nyert AS vetítő sugárnak meghatározzuk a képsíkkal való metszéspontját. Egy vonal vetületét vagy képét az egyes pontok vetületeinek geometriai helye adja. E szerint az egyenes vonalnak képe megint egyenes, t. i. a vetítendő egyenesen és S-en keresztül fektetett síknak a képsíkkal való metszésvonala.
A vetített sík három pontja akkor és csak akkor van egy egyenesben, ha képeik egy egyenesben vannak.
Mi a képsíkot úgy fogjuk választani, hogy párhuzamos legyen az S czentrumon és a vetítendő ábra e' egyenesén keresztül fektetett síkkal. Ekkor e' vetülete a képsíknak végtelen egyenese.
AB'CA'BC' hatszög vetülete tehát oly hatszög, a milyent 3. alatt vizsgáltunk, és az ott mondottaknál fogva P,Q és R képei egy egyenesbe esnek. De ez csak úgy lehetséges, hogy P,Q és R maguk is egy egyenesben vannak.
*Blaise Pascal franczia mathematikus és philosphus szül. Clermontban 1623. jun. 19., megh. Párisban 1662 aug. 19.