Kezdőlap


Cím:	A kör derékszögű projekcziója
Szerző(k):	Klug Lipót
Füzet:	1899/december, 65 - 69. oldal	PDF \| MathML
Témakör(ök):	Szakmai cikkek

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A következőkben két különböző bizonyítást mutatunk be arról a tételről, hogy a kör derékszögű projekcziója egy síkra ellipsis.

I. bizonyítás.

Kiindulunk abból a tételből, hogy egy pont polárisa egy körre vonatkozólag, a ponton keresztül fektetett szelőnek a körben fekvő részét ugyanolyan viszony szerint osztja, mint maga a pont az egész szelőt, azaz ha (1. ábra) a

H

pontnak

P Q

polárisa a

k

körre vonatkozólag a

H

ponton keresztül menő szelőt a

P'

pontban metszi, és a

H P'

szelőnek metszőpontjai a

k

körrel

D, E,

akkor

\begin{matrix} D P' : P' E = D H : E H . \end{matrix}

(1)

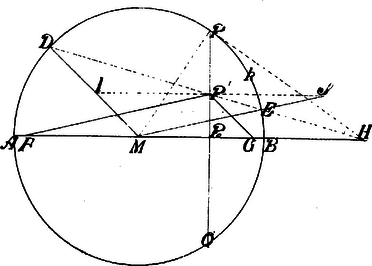1. ábra

Jelöljük a

k

körnek sugarát

a

-val, középpontját

M

-mel; az

M H

egyenes metszőpontjait a

k

körrel

A, B

-vel; az

M D, M E

körsugarak metszőpontjait a

P'

ponton keresztül menő és az

A B

átmérővel párhuzamos egyenessel

I, J

-vel, végre az

A B, P Q

egyenesek metszőpontját

P_{0}

-sal.
Minthogy

P' D I \sim H D M, P' E J \sim H E M

, azért

\begin{matrix} P' I : D P' = H M : D H \end{matrix}

(2)

\begin{matrix} P' E : J P' = H E : H M \end{matrix}

(3)

\begin{matrix} P' I : D I = H M : D M \end{matrix}

(4)

\begin{matrix} J E : J P' = M E : M H . \end{matrix}

(5)

Az (1), (2) és (3) aránypárok szorzatából következik

\begin{matrix} P' I = J P', \end{matrix}

ebből és a (4) és (5) aránypárok szorzatából következik

\begin{matrix} J E = D I . \end{matrix}

Ezen eredményeket tekintve

\begin{matrix} I M + J M = D M - D I + E M + J E = D M + E M = 2 a; \end{matrix}

ha a

P'

ponton keresztül menő és az

M I, M J

-vel párhuzamos egyenesek az

A B

átmérőt a

G, F

pontokban metszik, úgy hogy

\begin{matrix} G P' = M I, P' F = J M, P I' = G M, J P' = M F, \end{matrix}

akkor

\begin{matrix} G P' + P' F = 2 a . \end{matrix}

(6)

Ha a (2) és (3) aránypárt ekkép felírva

\begin{matrix} P' I : D P' = H M : D H \end{matrix}

\begin{matrix} J P' : P' E = H M : H E \end{matrix}

tagonként egymással szorozzuk a következő

\begin{matrix} P' I \cdot J P' : D P' \cdot P' E = {\bar{H M}}^{2} : D H \cdot H E \end{matrix}

(7)

aránypárt nyerjük.
És mert

\begin{matrix} D P' \cdot P' E = P P' \cdot P' Q = (P P_{0} - P' P_{0}) (P P_{0} + P' P_{0}) = {\bar{P P_{0}}}^{2} - {\bar{P' P_{0}}}^{2} \end{matrix}

\begin{matrix} D H \cdot H E = {\bar{P H}}^{2}, P' I = J P' \end{matrix}

\begin{matrix} H M : P H = M P : P P_{0}, \end{matrix}

azért (7)-ből származik

\begin{matrix} {\bar{P' I}}^{2} : {\bar{P P_{0}}}^{2} - {\bar{P' P_{0}}}^{2} = {\bar{M P}}^{2} : {\bar{P P_{0}}}^{2} \end{matrix}

vagy

\begin{matrix} {\bar{M F}}^{2} = {\bar{P' I}}^{2} = {\bar{M P}}^{2} [1 - {(\frac{P' P_{0}}{P P_{0}})}^{2}] . \end{matrix}

A nyert eredményből látható, hogy az

F, G

pontok helyzete az

A B

átmérőn csak a kör sugarától és azon viszonytól függ, mely szerint a

P'

pont a

P P_{0}

vonaldarabot osztja, azaz: ha a

k

kör pontjaiból az

A B

átmérőre bocsátott merőlegeseket állandó viszony szerint osztjuk, akkor az osztópontoknak az

F, G

pontoktól mért távolságai, (6) folytán, a kör átmérőjével egyenlő összeget adnak. Az osztópontok tehát oly ellipsisen feküsznek, melynek gyújtópontjai

F, G

és főtengelye

A B

.
Ha ezután a

k

kört az

A B

tengely körül tetszőleges szög alatt forgatjuk, a forgatott kör pontjait az eredeti síkra derékszög alatt vetítjük, akkor a nyert projekcziók az eredeti

k

kör pontjaiból az

A B

átmérőre bocsátott merőlegeseket állandó viszony szerint osztják és ezért a forgatott kör pontjainak projekcziói egy ellipsisen feküsznek.

II. bizonyítás.

Kiindulunk abból az ismert tételből, hogy egy forgáshenger síkmetszése ellipsis. Ennek bizonyítása a következő:
Egy forgáshengerbe (2. ábra)

F

gömböt írunk be, mely a hengert

φ

kör szerint és a metszősíkot

F

pontban érinti, azonkívül egy

G

gömböt, mely a hengert

γ

kör szerint, a metszősíkot

G

pontban érinti.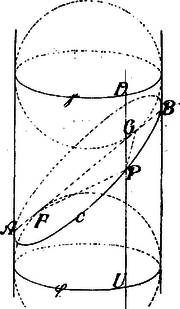

2. ábra

P

a metszősík és a henger

c

metszővonalának egy tetszés szerinti pontja, akkor

P

egy hengeralkotón fekszik, mely a

φ

kört

U

pontban, a

γ

kört

V

pontban metszi.
Minthogy egy pontból egy gömbhöz húzható érintők egyenlők, azért:

\begin{matrix} P F = P U, P G = P V \end{matrix}

és

\begin{matrix} P F + P G = P U + P V . \end{matrix}

U V

vonaldarab azonban a

P

ponttól független és egyenlő a

φ

és

γ

körök párhuzamos síkjainak távolságával, tehát a metszősík és a henger metszésgörbéje minden pontjának az

F, G

pontoktól mért távolságai állandó összeget adnak s mint ilyenek oly ellipszisen feküsznek, melynek gyújtópontjai az

F, G

pontok.
E segédtételt (mely Dandelin-től származik 1822-ből) így fejezhetjük ki:
Oly síkgörbe, melynek derékszögű projekcziója egy síkra kör, szükségképp ellipsis.
Ha kimutatható, hogy

k

kör derékszögű projekcziója

k'

egy síkra oly görbe, melynek derékszögű projekcziója bizonyos síkra egy

k''

kör, akkor a segédtétel alapján

k'

-nek ellipsisnek kell lennie.
E végből jelöljük (3. ábra)

k

kör sugarát

a

-val, középpontját

M

-mel, egy tetszés szerinti vonaldarabot

b

-ve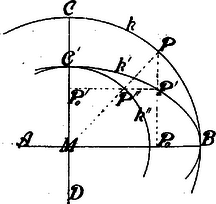l.

3. ábra

Bocsássunk a

k

kör

P

pontjából az

A B

átmérőre

P P_{0}

merőlegest és vegyünk fel ezen egy

P'

pontot akképpen, hogy

P P_{0} : P' P_{0} = a : b

. Bocsássunk a

P'

pontból az

A B

-re merőleges

C D

átmérőre egy

P' P'_{0}

merőlegest és határozzuk meg ezen a

P''

pontot akképpen, hogy

\begin{matrix} P' P'_{0} : P'' P'_{0} = P P_{0} : P' P'_{0} = a : b . \end{matrix}

E proporczióból következik (mert

P'_{0} M

párhuzamos és egyenlő

P' P_{0}

, továbbá

P' P'_{0}

párhuzamos és egyenlő

P_{0} M

\begin{matrix} P'_{0} M : P'' P'_{0} = P P_{0} : P'_{0} M = a : b, \end{matrix}

ebből az

M P P_{0}, P'' M P'_{0}

derékszögű háromszögek hasonlósága, tehát még

\begin{matrix} M P : M P'' = a : b, \end{matrix}

végre

\begin{matrix} M P'' = b . \end{matrix}

Ez eredményt ekképp fejezhetjük ki: ha

A B, C D

k

körnek két egymásra merőleges átmérője, és a

k

pontjaiból az

A B

-re bocsátott merőlegeseket állandó viszony szerint osztjuk, akkor az osztópontok egy

k'

görbén feküsznek; ha a

k'

pontjaiból a

C D

-re bocsátott merőlegeseket az előbbi állandó viszony szerint osztjuk, akkor az új osztópontok egy

k''

körön feküsznek.
Forgassuk ezek után a

k

kört az

A B

átmérő körül egy tetszés szerinti

φ

szöggel és projicziáljuk a forgatott

k

-t az eredeti síkra. A projekcziónak,

k'

-nek, pontja az eredeti

k

körnek pontjaiból az

A B

átmérőre bocsátott merőlegeseket állandó viszony szerint osztják. Ha a

k'

görbét az

A B

-re merőleges körátmérő körül szintén

φ

szög alatt forgatjuk és a forgatott görbét az eredeti síkra projicziáljuk, akkor a projekcziónak,

k''

-nek, pontjai a

k'

pontjaiból a

C D

-re bocsátott merőlegeseket szintén ugyanazon és az előbbivel egyenlő viszony szerint osztják. S mert a

k''

görbe az előbbiek szerint kör, azért a

k'

görbének, a segédtétel folytán, ellipsisnek kell lennie. A

k

kör derékszögű projekcziója

k'

, tehát ellipsis.
E bizonyításból következik még: ,,ha az

A

és a

B

sík a

C

síkhoz egyenlő szög alatt hajlik, a mellett az

A C, B C

síkok metszővonalai egymásra merőlegesek, és az

A

síkban fekvő kört a

C

síkra derékszög alatt projicziáljuk, akkor e projekcziónak derékszögű projekcziója a

B

síkra szintén kör".