Cím: Vázlatok a mathematika történetéből: Archimedes 2.
Szerző(k):  Baumgartner Alajos 
Füzet: 1899/november, 41 - 44. oldal  PDF  |  MathML 
Témakör(ök): Egyéb írások

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

(Folytatás.)
 

Archimedes tudományosan foglalkozott az arithemtikával, geometriával és mechanikával, főleg e két utóbbival. Nagyszámú kutatásait le is írta, s így eredeti műveiből teljesen biztos adatokat szerezhetünk munkálkodásairól. Művei azonban nem alkotnak valami összefüggő egészet vagy mathematikai rendszert, hanem inkább egyes értekezések. Teljesség kedvéért ugyan felemlítjük műveit, de nem taglaljuk azokat egyenkint, hanem inkább csak összefoglalásképpen ismertetjük működésének eredményeit. Még meglevő művei ezek: 1. Két könyv a síkok egyensúlyáról (súlypontmeghatározások), ezek közé van ékelve egy értekezés a parabola négyszögesítéséről. 2. Két könyv a gömbről és a hengerről. 3. A körmérés. 4. A csigavonalak. 5. A konoidok és szferoidok. 6. A homokszámítás. 7. Két könyv az úszó testekről. 8. Tételek.
Geometriai szempontból talán épp az utoljára említett műve a legérdekesebb; ez 15 tételt tartalmaz és arab feldolgozásban maradt meg, melyet később latinra fordítottak (Liber assumptorum). A 4. 5. és 6. tétel egy arbelus nevű idommal foglalkozik. Ez úgy keletkezik, hogy egy derékszögű háromszög átfogója és az átfogónak a magassága által képezett szeletei fölé ugyanazon oldalra eső félköröket rajzolunk. Az e három félkör által bezárt terület az arbelus, mely az átfogóhoz tartozó magasságra mint átmérőre rajzolt kör területével egyenlő.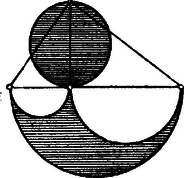
 

 

Az arbelus területe ugyanis:
T=πc28-(πx28+πy28),
ha c az átfogó és x meg y az átfogó szeletei; mivel:
x+y=c,
azért
x2+y2=c2-2xy;
ezt behelyettesítve a terület képletébe, lesz:
T=xyπ4.
De mivel az x és y szeleteknek az m magasság a mértani középarányosa s így:
xy=m2,
ennélfogva:
T=m2π4.
Az arbelus területe tehát csakugyan oly kör területével egyenlő, melynek átmérője a derékszögű háromszög átfogójához tartozó magasság.
A 8. tétel a triszekczióval áll kapcsolatban és így szól: ha egy AB húrt egy körön kívül meghosszabbítunk és meghosszabbítására BC=r vagyis a kör sugarával egyenlő darabot rámérünk és most a C pontot a kör O középpontjával egyenes vonallal összekötjük, mely a kört D és E pontokban metszi, akkor a BE ív harmadrésze az AD ívn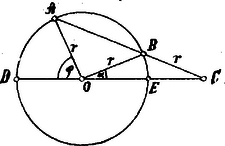ek.
 

 

Ugyanis OBC háromszög egyenlőszárú háromszög s így:
BCE∠=BOE∠=α,
ennélfogva e két szög külső szöge:
ABO∠=2α;
mivel azonban az AOB háromszög szintén egyenlőszárú háromszög, azért BAO∠ is =2α, az AOB középponti szög értéke pedig: 180∘-4α. Továbbá a φ, a 180∘-4α és az α szög összege a rajzból kitetszőleg 180∘, miből φ=3α, tehát csakugyan:
AD^=3BE^.
A szögnek három egyenlő részre való osztása már most eme tétel alapján a következő módon végeztetnék: a körbe illesztett szög egyik szárát (OD) a csúcson túl meg kell hosszabbítani a körön kívül is, a körív másik végpontjából pedig oly húrt beilleszteni, hogy ez a körön kívül a kör sugarával egyenlő távolságban messe az előbbi egyenest C pontban. Ez a feladat ismét példája annak az eljárásnak, melyet a görögök beillesztésnek, betolásnak neveztek és melyet akkor használtak, ha a feladatot vonalzó és körző nélkül nem bírták megoldani, szóval mikor a mai értelemben vett szerkesztést nem voltak képesek végezni.
Nevezetes tétel a 11. is: ha egy körben két húr egymásra merőleges, akkor a négy szelet négyzetének összege egyenlő a kör átmérőjének négyzetével. (K.M.L.VI.95.l.)
A 14. tétel tárgya egy salinon nevű különös idom. Ez úgy származik, hogy egy félkör középpontját egy másik kisebb és kifelé rajzolt félkör középpontjául felhasználjuk, a megmaradt átmérő szeletekre pedig mint átmérőkre befelé félköröket rajzolunk.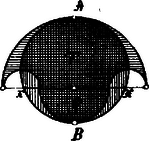
 

 

E salinon területe oly kör területével egyenlő, melynek átmérője az eredeti félkör és a kifelé rajzolt félkör sugarainak összege (AB). Legyen az eredeti félkör sugara r, a kifelé rajzolt félköré ρ, a külső szeletek pedig x, akkor a salinon területe:
T=r2π2+ρ2π2-x2π4;
de
x=r-ρ,
mit behelyettesítve, kapjuk:
T=π(r+ρ)24.

A salinon nevét némelyek a σαλoϱ (a tenger hullámzása) görög szóból származtatják, mert az idom határvonalai hullámvonalat alkotnak, de valószínűbb az, hogy a repkény görög nevével σελινoν, áll kapcsolatban, a mely növény leveléhez hasonlít némileg az idom.