Cím:	Vázlatok a mathematika történetéből: Euklides 7.
Szerző(k):	Baumgartner Alajos
Füzet:	1899/március, 113 - 117. oldal	PDF  |  MathML
Témakör(ök):	Egyéb írások

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. "Elemek": XI. XII. és XIII. könyv.   Euklides nagy művének utolsó főrészét a XI., XII. és XIII. könyv alkotja; tartalmuk a stereometria. A tárgyilag ismét összefüggő, mind a három könyvhöz tartozó definíciókat a XI. könyv tartalmazza. Az 1. definíció szerint: Test az, a minek hosszúsága, szélessége és mélysége van. A 3-8. definíció a síkok különféle helyzetét tárgyalja. A 9. és 10. definíció a hasonló és egybevágó testekről szól. A további definíciók a különböző testekre vonatkoznak, még pedig a 12. a gúlára, a 13. a hasábra, a 14-17. a gömbre, a 18-20. a kúpra, a 21-23. a hengerre, végre a 25-29. az öt szabályos testre. A XI. könyv 1-19. feladatai különböző stereometriai tételek az egyenesre és a síkra vonatkozólag. A 20-23. feladatok a testszögletről szólnak. A 29. feladat tartalma az a tétel, hogy egyenlő alapú és magasságú parallelepipedek egyenlők. A 33. feladat: Hasonló testek úgy aránylanak egymáshoz, mint megfelelő oldalaik köbei. A könyvben összesen 40 feladat van. A XII. könyv a testek köbtartalmát méri. Az 1. feladat kimondja ezt a planimetriai tételt: A körbe írt hasonló sokszögek úgy aránylanak egymáshoz, mint a körök átmérőinek négyzetei. Euklides ezt úgy bizonyítja be, hogy a hasonló sokszögek egy-egy megfelelő csúcspontját felhasználja az átmérő egyik végpontjául, a megfelelő szomszédos csúcspontokat pedig összeköti az átmérő másik végpontjával; azután kimutatja e háromszögek hasonlóságát és ezek révén jut el a tételhez. A 2. feladat annyiban nevezetes, a mennyiben Euklides egyik mathematikai módszerét világítja meg teljességében. A feladatban foglalt tétel, melyet különben már Hippokrates is ismert (V. évf. 25. lap), így szól. A körök úgy aránylanak egymáshoz, mint átmérőik négyzetei. A tétel levezetésében az előbbi feladat tételéből indul ki és a körök közé és a körökbe rendre szabályos négy-, nyolcz-, tizenhat-, stb. szögeket ír, minden esetben kimutatva, hogy a beírt sokszög oldalához tartozó körszelet kisebb, mint az ezen oldalra, mint alapra $\left(AB\right)$ rajzolt és a kör közé írt megfelelő sokszög oldala által határolt téglalap ($ABCD)$, de viszont nagyobb, mint e téglalap fele (az $AEB$ háromszög). 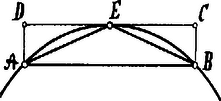    Ha ezt így folytatjuk, végre oly kis körszeleteket kapunk, melyek együttvéve kisebbek bármily kis felületnél. E helyen értjük csak meg, hogy miért fogalmazta meg Euklides a X. könyv 1. feladatát (VI. évf. 98. lap) oly módon, mint a milyenben ott megismertük. Nemcsak ez egy esetben és nem először találkozunk e helyen ily körülményes eljárással: a III. könyv 16. feladatánál (VI. évf. 61. lap) behatóan beszéltük meg a határátmenet módszerét; itt újra ráakadunk. Mindkét esetben a körvonal görbe volta idézte fel és okolta meg szükségét. Euklides maga ugyan nem e módszer megalapítója, de annak teljes mathematikai szigorúsággal operáló végrehajtója. A módszer csíráit már a Kr. e. V. században találtuk meg Antiphonnál és Brysonnál (V. évf. 4. és 5. lap), de a mathematikai meggondolás és szigorúság hiánya, meg elhamarkodottságuk, helytelen eredményre vezette őket. Euklides azonban biztosan halad előre, soha ugrást nem tesz, teljesen be nem bizonyított állítást nem kockáztat, hanem bizonyítás és meggyőzés dolgában inkább többet ad a jóból, semmint keveset. Euklides módszerét, mely tehát abban áll, hogy egyik mennyiségből egy másikra fokozatosan tér át, a XVII. században exhaustionak (kimerülés, kifáradás) nevezték el; magyarul még megközelítési módszernek is mondhatjuk. A 3-9. feladatok a gúláról szólnak; köztük legnevezetesebb a 7. feladat: Minden háromszögalapú hasáb három egymással egyenlő, háromszögalapú gúlára bontható fel. (Eudosxus tétele: V. évf. 119. lap). A 10.12. a kúp, a 13. a henger, a 14. és 15. feladatok pedig a kúp és henger köbtartalmi viszonyait tárgyalják. A 17. feladat tárgya a gömb és a beírt soklapú test, végre a 18. feladat ez: A gömbök úgy aránylanak egymáshoz, mint átmérőik köbei. Euklides természetesen e tételt is exhaustio segélyével bizonyítja be. A XIII. könyv a szabályos testeket tárgyalja; az ezeket határoló szabályos sokszögekkel a könyv első 12 feladata foglalkozik. Ezek között az első 5 feladat vonatkozással a szabályos ötszögre az aranymetszés számbeli viszonyait tárgyalja. Érdemes az egyik ily tételt szószerint bemutatni, pl. az 1. feladatét: Ha egyenest folytonos arányban metszünk: a nagyobbik darab megtoldva az egésznek felével, négyzetben öt akkora, mint az egésznek a fele. E definíciók tehát alapjukban véve tullajdonképpen szavakba fűzött képletek. E nevezett tételnek képlete ez: $\begin{array}{c}{\displaystyle {\left(x+\frac{a}{2}\right)}^2=5{\left(\frac{a}{2}\right)}^2\mathrm{,}}\end{array}$ miből $\begin{array}{c}{\displaystyle x+\frac{a}{2}=\frac{a}{2}\sqrt[]{5}\mathrm{.}}\end{array}$ Hasonló módon a további feladatok e képleteket magyarázzák: 3. $\begin{array}{c}{\displaystyle y+\frac{x}{2}=\frac{x}{2}\sqrt[]{5}\mathrm{.}}\end{array}$ 4. $\begin{array}{c}{\displaystyle a^2+y^2=3x^2\mathrm{.}}\end{array}$ 5. $\begin{array}{c}{\displaystyle a^2=x\left(a+x\right)\mathrm{,}}\end{array}$ hol $a$ az egészet, $x$ a nagyobbik, $y$ a kisebbik részt jelenti. A 12. feladat szerint a szabályos háromszög éle: $\begin{array}{c}{\displaystyle a=r\sqrt[]{3}\mathrm{,}}\end{array}$ ha $r$ a háromszög köré írt kör sugara. Ily szavakba fűzött képletek adják meg az összefüggést a szabályos testek élei ($a)$ és a körülírt gömb átmérője ($d)$ között a következő feladatokban. 13. a tetraëdernél: $d^2=\frac{3}{2}{a}^2$, 14. az oktaëdernél: $d^2=2a^2$, 15. a koczkánál: $d^2=3a^2$; a 16. feladat szerint az ikozaëder oldala egy ,,kisebb irracionalis" mennyiség; ez alatt Euklides olyanokat ért, melyekben a $\sqrt[]{\frac{5-\sqrt[]{5}}{2}}$ előfordul; a 17. feladat a dodekaëder oldalát apotom mennyiségnek mondja. Végre a könyvet befejező 18. feladat összehasonlítja az öt szabályos testet.   XIV. és XV. könyv.   E két könyv a XIII. könyvet egészíti ki, a mennyiben mindkettő a szabályos testeket tárgyalja. Mint már említettük, alexandriai Hypsiklest tartják a két könyv szerzőjének, ki azokat Kr. e. 180 körül írhatta és csatolta azokat Euklides művéhez; ámbár újabb vélemény is merült fel, mely szerint a két könyv közül csak az egyik lenne Hypsiklesé, a másik pedig egy a Kr. utáni VI. században élt író (Damascius) műve. A XIV. könyvnek majdnem mind a 7 feladata a dodekaëder és ikozaëder felületi és köbtartalmi viszonyait tárgyalja. A XV. könyvben végre a szabályos testek bizonyos kombinációi foglaltatnak, a mennyiben a feladatok ezek: 1. Adott koczkába tetraëdert írni;   2. "  tetraëderbe oktaëdert  "   3. adott koczkába oktaëdert írni;   4. "  oktaëderbe koczkát  "   5. "  ikozaëderbe dodekaëdert írni. A 6. feladat a szabályos testek éleinek és csúcsainak számát adja meg, végre a 7. feladat tárgya a szabályos testek lapszögeinek meghatározása szerkesztés útján.   Baumgartner Alajos.