Cím:	Vázlatok a mathematika történetéből: Euklides 4.
Szerző(k):	Baumgartner Alajos
Füzet:	1898/december, 61 - 64. oldal	PDF  |  MathML
Témakör(ök):	Egyéb írások

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. Euklides.   "Elemek": III. könyv.   A III. köny a kört tárgyalja; bevezetése 11 definíció, melyek a körök érintési viszonyaira és a kör részeire vonatkoznak. Az 1. feladat a kör középpontjának megkeresése; a következő feladatok tartalma külömböző tételek a kör húrjaira (2.3.4.), belső és külső pontokból vont egyenesekre (7.8.9.) körök érintkezésére (11.12.13) vonatkozólag. Érdekes a 16. feladat fogalmazása: A kör átmérőjére, annak végpontjában emelt merőleges kívül esik a körön, eme egyenes és a kerület közötti helyre más egyenes nem eshetik; az átmérő és a félkör által képezett szög minden egyenesvonalú helyes szögnél nagyobb, a maradéka pedig minden hegyes szögnél kisebb. E fogalmazást csak úgy érthetjük meg, ha visszatérünk Euklidesnek a szögre vonatkozó definícióira, melyek az I. könyvben a 8. és 9. számúak. A 8. definíció (K.M.L.VI. évf. 3. lap) szerint bárminő vonalak képeznek szögeket, tehát nemcsak egyenesek, melyekről külön a 9. definíció emlékezik meg: Ha a szöget képező vonalak egyenesek, a szöget egyenesvonalúnak mondjuk. A görbevonalú szögek méréséről azonban Euklides nem tesz említést, a III. könyv 7. definíciójában ismét érinti a dolgot ily módon: A körszelet szöge az a szög, melyet az egyenes (a 6. definíció értelméből kifolyólag: a húr) és a kör kerülete képez. A fentebb idézett 16. feladatban azonban előáll e szög mérésének szüksége, még pedig abban az esetben, mikor a húr átmegy az átmérőbe. Euklides csak úgy képes az átmérő és a körkerület által bezárt szöget tárgyalni, ha a húrt addig forgatja, míg ez az átmérővel esik össze és ily módon téríti el a szöget is a derékszögbe. Euklides érzi, hogy más módon nehézségei támadnak; ugyanis a görbe vonalú szög mérését teljesen elejti, mert nem említi fel, hogy a görbevonalú szöget is tulajdonképpen az az egyenesvonalú szög méri, melyet a görbék metszési pontjában a görbékhez vont érintők képeznek. E nehézség még jobban kitűnik az idézett feladat végpasszusában említett, az átmérőre merőleges egyenes és a körkerület által képezett szögnél: Euklides itt ugyanis nem mondhatja, hogy a körív összeesik az egyenessel, mert hiszen a körívnek csak egy közös pontja van az illető egyenessel, viszont a körívben e közös ponton kívül más pontot sem vehet fel, a melyből a közös ponthoz vont összekötő egyenes mérné a kérdéses szöget, mert ez az összekötő egyenes viszont nem esik egybe a körívvel és a szög is változik az illető pont helye szerint. Ha Euklides valamely definíciójában az általános görbe érintőjére támaszkodott volna, a feladat eme részét mindenesetre így fogalmazza: az átmérőre, annak végpontjában emelt merőleges vonal összeesik a kör érintőjével, így ellenben kénytelen volt a szög mérését úgy kifejezni, hogy az átmérőre merőleges egyenes és a körkerület által képezett szög ,,minden egyenesvonalú szögnél kisebb". E kifejezés azonban teljesen pontos és mathematikailag helyes; Euklides finom mathematikai érzéke a nehézségek közepette is a helyes úton vezette őt; különben emez eljárása nem is oly véletlenszerű, mint a hogy talán első pillanatra annak látszik, hanem egy egészen rendszeres mathematikai módszernek, a határátmenetnek egyik esete. Egyébiránt e feladat a XVI. és XVII. században még sok alkalmat nyújtott megvitatásokra, melyekben Clavius, Peletarius, Taquet, Vieta, Wallis és mások vettek részt. A 17. feladatban a körhöz egy külső pontból érintőt kell vonni; Euklides e szerkesztést igen érdekes módon végzi a kör szimmetrikus voltánál fogva: az adott kör $E$ középpontjából új kört rajzol, mely a külső $A$ ponton megy keresztül (1. ábra). 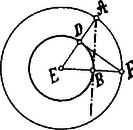    Az $AE$ sugár az adott kört $D$ pontban metszi; e pontban merőlegest emel a sugárra, mely merőleges a külső kört $F$ pontban metszi. Az $FE$ sugár az adott kört $B$ pontban metszi, mely $B$ pont lesz az $A$ pontból a körhöz vont érintőnek érintőpontja. A 18. és 19. feladat szintén az érintőre vonatkozó tételek. A 20. feladat az a nevezetes tétel, hogy a középponti szög kétszer akkora, mint az ugyanazon ívhez tartozó kerületi szög; ennek következményét pedig, hogy az ugyanazon íven nyugvó összes kerületi szögek egyenlők, a 21. feladat mondja ki. A 22. feladatnak az a tétele, hogy a körbe írt négyszög két-két átellenes szögének összege ${180}^{\circ }$. A 23. 24. és 25. feladat a körszeletekkel foglalkozik, a 26. 27. 28. és 29. pedig ismét az ívekkel és a hozzájuk tartozó szögekkel. Nevezetes tétel van ismét a 35. feladatban, mely szerint: Ha a körben két egyenes metszi egymást, az egyiknek szeletei által képezett téglalap egyenlő a másiknak szeletei által képezett téglalappal. E tételt, mint tudjuk, már Archytas ismerte és alkalmazta is (l. K.M.L. V. évf. 83. lap). A 36. és 37. számú utolsó feladat tárgya az a tétel, hogy egy külső pontból a körhöz vont szelők szeleteinek szorzata egyenlő az érintő négyzetével.   IV. könyv.   E könyv a körbe és a kör köré írt idomokat tárgyalja és így mintegy folytatását és kiegészítését képezi a III. könyvnek. A könyv elején 7 definíció van a körbe és a kör köré való írásról. A kis terjedelmű könyvből ezek az említésre méltó feladatok: 4. Adott háromszögbe kört írni. 5. Adott háromszög köré kört írni. 6. Adott körbe négyzetet írni. 7. Adott kör köré négyzetet írni. 8. Adott négyzetbe kört írni. 9. Adott négyzet köré kört írni. A 10. feladat ismét az aranymetszést alkalmazza, mert oly egyenlőszárú háromszöget kell szerkeszteni, melyben az alap mellett fekvő mindegyik szög két akkora legyen, mint a harmadik szög. Ez, mint tudjuk a ${72}^{\circ }\mathrm{,}{72}^{\circ }\mathrm{,}{36}^{\circ }$ szögekkel bíró háromszög, mely a szabályos ötszögnek alkotó eleme és úgy keletkezik benne, ha a szabályos ötszög egyik oldalának két végpontját összekötjük az oldallal szemben fekvő csúcsponttal. Eme összefüggés alapján végzi is Euklides a szabályos ötszög szerkesztését a 11. feladatban. A 12. 13. és 14. feladat is az ötszögre vonatkozik. A 15. feladatban a szabályos hatszöget, a 16. és utolsó feladatban pedig a szabályos ötszög és a szabályos háromszög csúcspontjainak segélyével a szabályos tizenötszöget szerkeszti.   Baumgartner Alajos.