Cím:	Vázlatok a mathematika történetéből: Euklides 3.
Szerző(k):	Baumgartner Alajos
Füzet:	1898/november, 41 - 45. oldal	PDF  |  MathML
Témakör(ök):	Egyéb írások

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. Euklides.   "Elemek": II. könyv.   A II. könyv terjedelemre nézve a legkisebb ugyan, de tartalom tekintetében egyike a mű legtanulságosabb részeinek, mert anyaga oly természetű, hogy bepillantást nyerünk az egész görög mathematikai felfogásba és módszerbe. Mielőtt e könyv részletes tárgyalásába belefognék, némi magyarázatot kell előrebocsátanom. Az eddigiekből láttuk, hogy az irrationális mennyiségek mily fontos szerepet játszottak már Pythagoras óta a mathematikusok tanulmányaiban. Nagyon korán vették észre, hogy e számok tulajdonképpen ki nem fejezhetők, "kimondhatatlanok" (IV. évf. 145. lap) és e miatt a velük való számítás is kivihetetlen. A görögök általánosítási törekvéseinek e mennyiségek tehát utjokban állottak: a mai értelemben vett általánosított mennyiségtan, algebra, nem fejlődhetett ki. Viszont figyelmen kívül sem lehetett hagyni e mennyiségeket, mert minduntalan felléptek. E "kimondhatatlan" mennyiségeknek ama tulajdonsága azonban, hogy geometriailag minden nehézség nélkül ábrázolhatók, mégis módot nyujtott arra, hogy velük foglalkozhassanak. A görög mathematikusok tehát teljesen elejtették e mennyiségek számbeli jellegét és tisztán geometriai jelentésükkel foglalkoztak. Miután minden ily "kimondhatatlan" mennyiség, mint pl. $\sqrt[]{2}\mathrm{,}\sqrt[]{3}\mathrm{,}\sqrt[3]{2}\mathrm{,}$ stb., geometriailag kifejezhető volt, az általános mennyiségek kifejezésére is a geometriai ábrázolás útjára tértek. Ha e "kimondhatatlan" mennyiségeket a görögök vagy még jobban vagy sehogysem ismerték volna, minden valószínűség szerint tisztán abstrakt algebra fejlődik ki náluk; így pedig, mivel azt találták, hogy minden mennyiségnek van geometriai értelme, minden mathematikai fejtegetésüknek geometriai mezt kölcsönöztek és megteremtették ez által a geometriai algebrát. Ily geometriai algebrát tartalmaz az "Elemek" II. könyve, melynek még egy gyakran előforduló kifejezésével kell megismerkednünk: ez a gnomon. A pythagoreusok azt a térdalakú idomot nevezték gnomonnak, mely fennmarad, ha egy négyzetből egy kisebb négyzetet kivágunk, de úgy, hogy a két négyzet egyik csúcsa és az ennél levő derékszög egymást födje. Ők leginkább azokkal a négyzetekkel foglalkoztak, melyek közül a nagyobbiknak oldala $1$ egységgel hosszabb, mint a kisebbiknek $n$ egységnyi oldala; ekkor a nagyobb négyzet tudvalevőleg $2n+1$ négyzetegységgel nagyobb a kisebbnél; innen ered az, hogy a pythagoreusok idejétől kezdve a páratlan számokat gnomon-számoknak is nevezték. Euklides a II. könyv 2. definícziójában a gnomon fogalmát kibővíti, a mennyiben ezt mondja: Minden prallelogrammban az átló körüli egyik parallelogrmmot két pótlékával együtt gnomonnak nevezzük. A fogalmazás kissé nehézkes; a mellékelt ábra alapján azonban minden nehézség és további magyarázat nélkül megértjük.     Még csak avval kell tisztában lennünk, hogy egy vonalra rajzolt négyzet általában egy számnak második hatványát, két vonal téglalapja pedig két számnak szorzatát jelenti; ezzel áttérhetünk a II. könyv részleteibe, mely könyv, mint már említettem, lényegében algebra, de formában geometria és melynek eszköze és módszere a területek alkalmazása, vetése $\left(\pi \alpha \rho \alpha \beta \text{o}\lambda \eta \text{'}\right)$. Az 1. feladat ez: Ha van két egyenes és az egyiket bárhány részre osztjuk: az adott két egyenes téglalapja egyenlő az osztatlan egyenes és a felosztott egyenes mindegyik szeletének téglallapjaival. A szövegezés ily geometriai formában kissé nehézkes; sokkal egyszerűbben érteti meg a tételt a mai modern algebrai jelölésünk: ha $\begin{array}{c}{\displaystyle b=p+q+r+\text{...}\mathrm{,}}\end{array}$ akkor $\begin{array}{c}{\displaystyle ab=ap+aq+ar+\text{...}}\end{array}$ A 2. feladat: Ha egy egyenest bárhol elmetszünk, az egész egyenes és mindegyik szeletének téglalapjai egyenlők az egésznek négyzetével. Modern jelöléssel: ha az $a$ szeletei $x$ és $a-x$, akkor $\begin{array}{c}{\displaystyle ax+a\left(a-x\right)=a^2\mathrm{.}}\end{array}$ A 3. feladat értelme ez: $\begin{array}{c}{\displaystyle ax=\left(a-x\right)x+x^2\mathrm{.}}\end{array}$ A 4. feladat szószerint ez: Ha egy egyenest bárhol elmetszünk: az egésznek négyzete egyenlő a szeletek négyzeteivel meg a szeletek által befogott kétszeres téglalappal. Rögtön ráismerünk a kéttagú összegre vonatkozó jól ismert képletünkre: $\begin{array}{c}{\displaystyle a^2=x^2+y^2+2xy\mathrm{,}}\end{array}$ ha $\begin{array}{c}{\displaystyle a=x+y\mathrm{.}}\end{array}$ Rendkívül fontos az 5. feladat: Ha egy egyenest megfelezünk és azonkívül még két nem egyenlő részre osztunk: a nem egyenlő szeletek által képezett téglalap meg a felező- és a másik osztási pont közötti távolság négyzete együttvéve annyi, mint az egész távolság felének a négyzete. Mai jelölésünkben ez: $\begin{array}{c}{\displaystyle \left(a-x\right)x+{\left(\frac{a}{2}-x\right)}^2={\left(\frac{a}{2}\right)}^2\mathrm{.}}\end{array}$ A régiek e feladatot ennek az alaknak: $\begin{array}{c}{\displaystyle {\left(\frac{a}{2}\right)}^2-{\left(\frac{a}{2}-x\right)}^2=ax-x^2=b^2}\end{array}$ az értelmében így fogalmazták: egy adott egyenesre annak részével téglalap szerkesztendő, úgy hogy a rész négyzetét belőle kivonva, adott négyzetet $\left(b^2\right)$ kapjunk. Ezt nevezték az elliptikus felületvetésnek $(\epsilon \lambda \lambda \epsilon \iota \varphi \iota \sigma$, hiány). A 6. feladatban kifejezett tétel viszont arra a szerkesztésre vonatkozik, hogy a nevezett téglalap egy négyzetalakú idommal meghaladja az adott egyenesre szerkesztett téglalalpot. Ez volt a hiyperbolikus felületvetés ($\nu \pi \epsilon \rho \beta \text{o}\lambda \eta \text{'}$, túldobás, fölösleg). A tétel mai írásmódunkban ez: $\begin{array}{c}{\displaystyle \left(a+x\right)x+{\left(\frac{a}{2}\right)}^2={\left(\frac{a}{2}+x\right)}^2\mathrm{.}}\end{array}$ Látnivaló tehát, hogy az 5. és 6. feladat az $ax-x^2=b^2$ és $ax+x^2=b^2$ alakú vegyes másodfokú egyenletek tárgyalását foglalja magában. A következő feladatoknál elégségesnek tartom csakis a feladatok értelmét a mai algebrai jelölésünk segélyével megadni: 7. feladat: $a^2+x^2=2ax+{\left(a-x\right)}^2;$ 8. feladat: $4ax+{\left(a-x\right)}^2={\left(a+x\right)}^2;$ 9. feladat: ${\left(a-x\right)}^2+x^2=2{\left(\frac{a}{2}\right)}^2+2{\left(\frac{a}{2}-x\right)}^2;$ 10. feladat: ${\left(a+x\right)}^2+x^2=2{\left(\frac{a}{2}\right)}^2+2{\left(\frac{a}{2}+x\right)}^2\mathrm{.}$ A 11. feladat az aranymetszést tárgyalja, valószínűleg abban az alakban, a melyet már Eudoxus (l. V. évf. 120. lap) adott e feladatnak. Fontosságánál és érdekességénél fogva szószerint közlöm egészen a bizonyításáig: Messünk egy adott egyenest úgy, hogy az egésznek és az egyik szeletnek téglalapja egyenlő legyen a másik szelet négyzetével. Legyen az adott egyenes $AB$; ezt úgy kell metszeni, hogy az egész és az egyik szelet által képezett téglalap egyenlő legyen a másik szelet négyetével.     Rajzoljuk $AB$ egyenesre $ABCD$ négyzetet és felezzük meg $AC$-t $E$ pontban, vonjuk meg $EB$-t, hosszabbítsuk meg $CA$-t $F$-ig úgy, hogy $EF$ egyenlő legyen $EB$-vel; rajzoljunk $AF$-re $AFGH$ négyzetet és hosszabbítsuk meg $GH$-t $K$-ig: azt mondom, hogy a $HBDK$ téglalap egyenlő az $AFGH$ négyzettel. Rendkívüli fontossága van a 12. és 13. feladatnak, mert ezek határozottan a Carnot-tételt tartalmazzák a tompa és a hegyesszögű háromszögekre nézve, természetesen a goniometriai kifejezések nélkül. Nem lesz érdektelen, legalább az egyik, pl. a 13. feladatot eredeti fogalmazásában megismerni: A hegyesszögű háromszögekben a hegyes szöggel szemközti oldal négyzete a hegyes szöget bezáró oldalok négyzeteinél a hegyes szöget bezáró egyik oldal és ennek a magasságvonal által elmetszett a hegyes szög melleti szelete által képezett kétszeres téglalappal kisebb. A II. könyv 14. és egyszersmind utolsó feladata ez: Szerkesszünk adott egyenes vonalú idommal egyenlő négyzetet. A megoldás menete az, hogy az idomot felosztjuk háromszögekre, melyek az I. könyv különböző feladatai alapján könnyen alakíthatók át téglalapokká; miután így tehát az eredeti idommal egyenlő téglalapot nyertünk, még csak a téglalappal egyenlő négyzetet kell szerkesztenünk, mely szerkesztést Euklides így végzi. 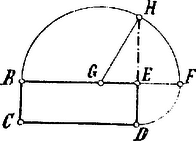    Legyen az adott téglalap $BEDC$; hosszabbítsuk meg $BE$ oldalát $F$-ig, úgy hogy $EF$ egyenlő legyen $ED$ oldallal; felezzük meg a $BF$ oldalt $G$ pontban, rajzoljunk e pontból mint középpontból félkört, hosszabbítsuk meg $DE$-t $H$-ig, akkor $EH$ lesz a $BEDC$ téglalappal egyenlő négyzet oldala.   Baumgartner Alajos.