| Cím: | Vázlatok a mathematika történetéből: Euklides 2. | ||
| Szerző(k): | Baumgartner Alajos | ||
| Füzet: | 1898/október, 25 - 28. oldal |  PDF | MathML PDF | MathML |
|
| Témakör(ök): | Egyéb írások | ||
|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. Euklides. "Elemek": I. könyv. (Folytatás.) A megfejtés vagy a bizonyítás igen beható, a legapróbb részletek felemlítésével. Euklides úgy ír, hogy a minden előtanulmány nélküli laikus is megérti; a levezetés lassú lépésekben halad előre, ugrások nélkül, biztosan, meggyőzően. Sok leírás helyett inkább példát mutatok be, a minek mindjárt az 1. feladat kínálkozik. Adott egyenesre szerkesszünk egyenlő oldalú háromszöget. Legyen az adott egyenes . Erre az egyenesre kell egyenlő oldalú háromszöget szerkeszteni. Az középpontból rajzoljunk távolsággal kört és középpontból távolsággal kört és a pontból, a melyben a körök egymást metszik, húzzunk az és pontokhoz és egyeneseket. 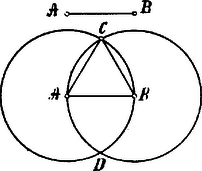 Minthogy az pont a körnek középpontja, egyenlő -vel; és mert a pont az körnek középpontja, egyenlő -val. Megmutattuk tehát, hogy egyenlő -vel, tehát mind , mind egyenlők -vel. De mivel ugyanavval egyenlők, egymással is egyenlők, egyenlő -vel; tehát mindhárman egyenlők egymással. Az háromszög tehát egyenlő oldalú és egyenesre van szerkesztve. Adott egyenesre tehát egyenlő oldalú háromszöget szerkesztettünk, a mit tenni kellett. Íme, szószerint az 1. feladat! Alaposság hiánya és gyors haladás miatt nincs okunk panaszkodni, de a miatt sem, hogy a feladatok elvégzése nagy szellemi megerőletetéssel járna; erre szolgáljon további például a 3. feladat: Két adott egyenes közül vágjunk el a nagyobbikból a kisebbikkel egyenlő darabot. Az első theoréma a 4. feladat: Ha két háromszögben egyiknek két oldala külön-külön egyenlő a másiknak két oldalával és az egyenlő oldalak által bezárt szög is egyenlő a másik szöggel, akkor a háromszögek harmadik oldalai is egyenlők egymással és a háromszögek is és a többi szögek is, melyeket az egyenlő aldalak bezárnak, egyenlők egymással. E feladat tárgyalja először a háromszögek egybevágóságát, ugyancsak erről szól még a 8. és a 26. feladat. A 9. feladat a szög, a 10. pedig az egyenes felezése. A 11. és 12. a merőleges emelése és bocsátása. A 15. a csúcsszögek egyenlősége. A 17. feladat: Minden háromszög bármely két szöge együttvéve kisebb két derékszögnél. A 20. feladat: Minden háromszög bármely két oldala együttvéve nagyobb a harmadiknál. A 27., 28., 29., 30. és 31. feladat a párhuzamos és az azokat metsző vonalakkal foglalkozik. A háromszög egyik legfontosabb tétele a 32. feladat. Minden háromszögben az egyik oldal meghosszabbíttatván, a külső szög egyenlő a másik két belső szöggel és a háromszög három belső szöge együttvéve két derékszöggel egyenlő. Mint tudjuk, ezt a tételt már Pythagoras ismerte (IV. évf. 125. lap) és bizonyítását is tőle vette át Euklides. A 33. és 34. feladat tárgya a parallelogramm. A 35. feladat ez: Egyenlő alapokon álló és ugyanazon párhuzamosok közötti parallelogrammok egymással egyenlők. E feladat megnyitja a területszámítási feladatok sorát a négyszögekre és háromszögekre vonatkozólag. (36.-46.) Az egész mű egyik legérdekesebb pontja végre a 47. feladat: a Pythagoras-féle tétel első bizonyítása, mely minden valószínűség szerint magától Euklidestől ered. A tételt kiváló mathematikai fontosságánál és történeti érdekességénél fogva teljességében közlöm. A derékszögű háromszögekben az átfogó négyzete egyenlő a befogók négyzeteink összegével. Legyen derékszögű háromszög, melynek szöge a derékszög: azt mondom, hogy a négyzete egyenlő a és négyzeteinek összegével. Mert írjunk -re -ra -re pedig négyzetet és vonjunk -n keresztül akár -vel, akár -vel párhuzamos egyenest és húzzuk meg az és az egyeneseket. 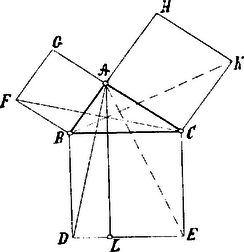 Minthogy mind a , mind a szögek derékszögek, de e mellékszögeket a egyenes és az pont különböző két oldalán fekvő meg egyenes teszi egyenlővé két derékszöggel: tehát és egy egyenesben fekszik. Ugyanezért és is egy egyenesben fekszik. És minthogy a szög egyenlő az szöggel, mivel mindkettő derékszög: adjuk hozzá mindegyikhez a közös szöget; e szerint az egész szög egyenlő az egész szöggel. És mivel egyenlő -vel, pedig -val, ennélfogva a és oldalak külön-külön egyenlők a és oldalakkal és a szög is egyenlő az szöggel: tehát az oldal is egyenlő az oldallal és az háromszög egyenlő az háromszöggel; de a téglalap kétszer akkora, mint az háromszög, mert közös alapjuk van és ugyanazon és párhuzamosok között vannak. négyzet pedig szintén kétszer akkora, mint az háromszög, mert közös alapjuk van és ugyanazon és párhuzamosok között vannak. Mivel pedig egyenlőknek kétszeresei egymással egyenlők: téglalap egyenlő négyzettel. Ha az és egyeneseket meghúzzuk, hasonlóképpen kimutathatjuk, hogy: téglalap egyenlő négyzettel; az egész négyzet tehát egyenlő a és négyzetekkel együttvéve. De négyzet -re van rajzolva, és négyzetek pedig -ra és -re, tehát a oldal négyzete egyenlő a és oldalak négyzeteivel. A derékszögű háromszögekben tehát az átfogó négyzete egyenlő a befogók négyzeteinek összegével, Q.E.D. A 48. feladat végre az előbbi feladat megfordítása: Ha a háromszög egyik oldalának négyzete egyenlő a másik két oldal négyzeteinek összegével, e két oldal derékszöget zár be. Ezzel az I. könyv be van fejezve.
|