Kezdőlap


Cím:	A háromszög ötödik nevezetes pontja
Szerző(k):	Rátz László
Füzet:	1898/szeptember, 5 - 7. oldal	PDF \| MathML
Témakör(ök):	Szakmai cikkek

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Ismeretes, hogy a háromszög magasságai, szögfelezői, középvonalai és az oldalak középpontjaiban emelt merőlegesek egy-egy pontban metszik egymást, mely pontokat a háromszög nevezetes pontjainak mondjuk.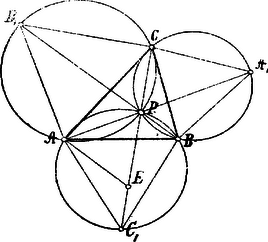
E négy ponton kívül van még egy, melyet érdekes tulajdonságai miatt a háromszög ötödik nevezetes pontjának szoktak nevezni. E pontnak -melyet $P$ -vel jelölünk- néhány nevezetesebb tulajdonságát a következőkben mutatjuk be.
$1^{\circ}$ E pontból a háromszög oldalai egyenlő szögek alatt látszanak, tehát $A P C ∢ = C P B ∢ = B P A ∢$ . Hogy $P$ -t megszerkeszthessük, rajzoljunk az $A B C$ háromszög oldalai fölé egyenlőoldalú háromszögeket; az ezen háromszögek csúcsain átmenő körök a keresett pontban metszik egymást.
Bizonyítás. $A C_{1} B P$ és $B A_{1} C P$ húrnégyszögek; $A C_{1} B ∢ = B A_{1} C ∢ = 30^{\circ}$ s így $A P B ∢ = B P C ∢ = 120^{\circ}$ . Ennélfogva $A P C ∢ = 120^{\circ}$ s minthogy $A B_{1} C ∢ = 60^{\circ}$ , azért $A P C B_{1}$ is húrnégyszög s így a harmadik kör is átmegy a $P$ ponton.

2^{\circ}

A A_{1}, B B_{1}

és

C C_{1}

egyenesek

P

pontban metszik egymást.
Bizonyítás.

A C A_{1} ▵ ≅ B C B_{1} ▵

; tehát

C B_{1} B ∢ = C A A_{1} ∢

s így

C B_{1} A P

húrnégyszög, melyben

A P C ∢ = 120^{\circ}

; hasonlóképp kimutathatjuk

A P B ∢ = B P C ∢ = 120^{\circ}

. E tételt is felhasználhatjuk a

P

pont megszerkesztésére.

3^{\circ}

A A_{1} = B B_{1} = C C_{1}

, mert

A C A_{1} ▵ ≅ B C B_{1} ▵

és

A B A_{1} ▵ ≅ C B C_{1} ▵

4^{\circ}

A A_{1} = B B_{1} = C C_{1} = A P + B P + C P

.
Bizonyítás. Minthogy

A P C_{1}

és

C_{1} P B

egyenlő húrokhoz

(A C_{1} = B C_{1})

tartozó kerületi szögek, azért

A P C_{1} ∢ = C_{1} P B ∢ = 60^{\circ}

. Ha

P

-ből

P C_{1}

-re rámérjük

A P

-t, úgy hogy

P E = A P

, akkor az

A P E

háromszög egyenlőoldalú s így

A E = A P

; de

A C_{1} = A B

és

A E C_{1} ∢ = A P B ∢ = 120^{\circ}

, tehát

A E C_{1} ▵ ≅ A P B ▵

, miért is

E C_{1} = P B

. Ennélfogva:

\begin{matrix} C C_{1} = C P + P E + E C_{1} = C P + A P + B P . \end{matrix}

5^{\circ}

A B C

háromszög síkjának összes pontjai közül a

P

pontnak a háromszög csúcsaitól való távolságainak összege a legkisebb. Ha tehát

X

A B C

síknak egy tetszés szerinti pontja, úgy

\begin{matrix} A P + B P + C P < A X + B X + C X . \end{matrix}

E tételt Riesz Frigyes, lapunk munkatársa, következőképpen bizonyítja:
Az

A, B, C

pontokban az

A P, B P

és

C P

egyenesekre emelt merőlegesek az

A' B' C'

szabályos háromszöget alkotják.
Jelöljük a tetszés szerint választott

X

pontnak

A' B' C'

háromszög oldalaitól való távolságait

x_{a}, x_{b}

és

x_{c}

-vel.
Minthogy az

A' B' C'

háromszög területe egyenlő a

B' X' C', C' X A'

és

A' X B'

háromszögek területeinek összegével, azért

\begin{matrix} \frac{a m}{2} = \frac{a}{2} (x_{a} + x_{b} + x_{c}), \end{matrix}

ha az

A' B' C'

háromszög alapja

a

, magassága

m

. Az egyenlet mindkét oldalát

\frac{a}{2}

-lel osztva, kapjuk hogy:

\begin{matrix} x_{a} + x_{b} + x_{c} = m = állandó \end{matrix}

s így

\begin{matrix} A P + B P + C P = x_{a} + x_{b} + x_{c} = m . \end{matrix}

X

A' B' C'

háromszög kerületén belül fekszik, úgy

\begin{matrix} X A ≧ x_{a}, X B ≧ x_{b}, X C ≧ x_{c} \end{matrix}

tehát

\begin{matrix} X A + X B + X C \geq x_{a} + x_{b} + x_{c} = A P + B P + C P . \end{matrix}

X A + X B + X C

összeg minimuma tehát

A P + B P + C P .

X

A' B' C'

háromszög kerületén kívül fekszik, úgy mindig találunk az

A B C

háromszög belsejében oly

X_{1}

pontot, melyre nézve

\begin{matrix} A X_{1} + B X_{1} + C X_{1} < A X + B X + C X . \end{matrix}

Legyen

X', X

pontnak tükörképe olyan oldalra, pl.

B C

-re, vonatkozólag, melytől távolsága negatív. (X távolsága

B C

-től positív, ha

X

pont a

B C

által két részre osztott síknak azon oldalán fekszik, melyen

A

; ellenkező esetben negatív.) Ekkor

B X' = B X, C X' = C X'

. Minthogy

A X X'

háromszög

A D

középvonala

X'

felé hajlik, azért

A X' < A X

, tehát

\begin{matrix} A X' + B X' + C X' < A X + B X + C X . \end{matrix}

X'

nem esik a háromszög belsejébe, ujbóli vagy többszörös transformatió után mindig nyerhetünk olyan

X^{(k)}

pontot, mely a háromszög belsejében fekszik s melyre nézve az

\begin{matrix} X^{(k)} + B X^{(k)} + C X^{(k)} \end{matrix}

kifejezésnek

k

növekedésével való folytonos kisebbedésénél fogva:

\begin{matrix} A X^{(k)} + B X^{(k)} + C X^{(k)} < A X + B X + C X . \end{matrix}

Minthogy pedig

\begin{matrix} A P + B P + C P < A X^{(k)} + B X^{(k)} + C X^{(k)}, \end{matrix}

egyszersmind

\begin{matrix} A P + B P + C P < A X + B X + C X, \end{matrix}

hol

X

A B C

sík tetszés szerinti pontja. Hogy pedig

X

a térnek is tetszés szerinti pontja lehet, abból következik, hogy

A X_{1} < A X, B X_{1} < B X, C X_{1} < C X,

X_{1}

vetülete

X

-nek az

A B C

síkra.