Kezdőlap


Cím:	Egy síkgeometriai tételről
Szerző(k):	Weisz Lipót
Füzet:	1898/június, 167 - 170. oldal	PDF \| MathML
Témakör(ök):	Szakmai cikkek

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

E czikkben egy általános síkgeometriai tétellel foglalkozunk, mely több, a háromszögekre, valamint az egymásra merőleges átlókkal bíró négyszögekre vonatkozó, ismeretes tételt foglal magában.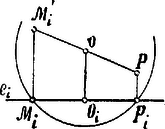
A tétel a következő:
Ha valamely $n$ -oldalú síkpoligon síkjában van olyan $P$ pont, melyből a poligon oldalaira a $P P_{1}, P P_{2}, ..., P P_{i}, ... P P_{n}$ merőlegeseket bocsátva, azoknak $P_{1}, P_{2}, ..., P_{i}, ... P_{n}$ talppontjain keresztül kör rajzolható, akkor e körnek a poligon oldalaival való újabb $M_{1}, M_{2}, ..., M_{i}, ... M_{n}$ metszéspontjaiban a megfelelő oldalakra emelt merőlegesek egy $M$ pontban találkoznak; a $P M$ egyenes keresztül megy ama kör $O$ középpontján és a $P O$ és $O M$ távolságok egyenlők.
A tétel a következőképpen bizonyítható:
Legyen $e i$ egyenes egy a kívánt tulajdonságú $P$ ponttal bíró poligon $i$ -edik oldala; az $O$ középpontú körnek az $e i$ egyenessel való metszéspontjai $P_{i}$ és $M_{i}$ ; $O_{i}$ az $O$ -ból $e_{i}$ -re bocsátott merőleges talppontja. Legyen végre az $M_{i}$ pontban $e_{i}$ -re emelt merőlegesnek $P O$ egyenessel való metszéspontja $M'_{i}$ .

O O_{i}

merőleges a

P_{i} M_{i}

húrra; tehát:

\begin{matrix} P_{i} O_{i} = O_{i} M_{i} \end{matrix}

De a

P P_{i}, O O_{i}

és

M'_{i} M_{i}

egyenesek merőlegesek lévén

e i

-re, párhuzamos egyenesek és így a párhuzamos szelők törvénye alapján:

\begin{matrix} P O : O M'_{i} = P_{i} O_{i} : O_{i} M_{i} \end{matrix}

vagyis

\begin{matrix} P O = O M'_{i} . \end{matrix}

i

-edik oldalra bemutatott eljárás minden oldalra érvényes lévén, az

M_{1}, M_{2}, ..., M_{i}, ... M_{n}

pontokban az

e_{1}, e_{2}, ..., e_{i}, ... e_{n}

oldalakra emelt merőlegesek valóban keresztül mennek azon

M

ponton, mely a

P O

egyenesen van és pedig úgy, hogy

P O = O M

.
A tétel a háromszögekre nézve következőképpen fogalmazható:
Ha valamely

A B C

háromszög síkjának egy tetszőleges

P

pontjából az oldalakra merőlegeseket bocsátunk, akkor e merőlegesek

A_{1}, B_{1}, C_{1}

talppontjain keresztül vezetett

O

középpontú körnek az oldalakkal való újabb metszéspontjain állított merőlegesek oly

M

pontban találkoznak, mely a

P O

egyenesen van és melyre nézve

M P = 2 M O

.
A tétel valóban érvényes a háromszög síkjának bármely pontjára nézve. Az általános fogalmazásnál előforduló

M_{1}, M_{2}, ..., M_{i}, ... M_{n}

poligon helyébe itt az

A_{1} B_{1} C_{1}

háromszög lép, mely köré ‐ mint minden háromszög köré ‐ mindig lehet kört rajzolni.
Itt megemlítjük, hogy a háromszögre speczializált tételnek van egy érdekes analogtétele, az ú. n. Reuschle-féle tétel, melyet e helyen bizonyítás nélkül közlünk:
Ha valamely

A B C

háromszög oldalain az

A_{1}, B_{1}, C_{1}

pontok úgy vannak választva, hogy az

A A_{1}, B B_{1}, C C_{1}

egyenesek egy pontban találkoznak, akkor az

A_{1} B_{1} C_{1}

háromszög köré írt körnek az

A B C

háromszög oldalaival való újabb metszéspontjai olyan

A_{2}, B_{2}, C_{2}

pontok, melyek a szemben fekvő csúcsokkal összekötve egy pontban találkozó

A A_{2}, B B_{2}, C C_{2}

egyeneseket adnak.
Alkalmazzuk már most tételünket arra a specziális esetre, midőn a tetszőlegesen választható

P

pont az

A B C

háromszög köré írható kör középpontja. Ekkor a

P A_{1}, P B_{1}, P C_{1}

merőlegesek

A_{1}, B_{1}, C_{1}

talppontjai a háromszög oldalait felező pontok és az ezeken átvezető

O

középpont kör az u. n. Feuerbach-féle kör. E körnek a háromszög oldalaival való újabb metszéspontjai ‐

A_{2}, B_{2}, C_{2}

‐ a magasságok talppontjai.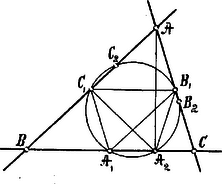

Valóban:

A_{1} B_{1} A C_{1}

négyszög parallelogramma lévén:

\begin{matrix} A_{1} B_{1} C_{1} ▵ ≅ A C_{1} B_{1} ▵ \end{matrix}

Másrészt

\begin{matrix} A_{1} B_{1} C_{1} ▵ ≅ A_{2} B_{1} C_{1} ▵ \end{matrix}

mert ugyanazon körben parallel húrok között feküsznek.
Tehát

\begin{matrix} A_{1} B_{1} C_{1} ▵ ≅ A_{2} B_{1} C_{1} ▵ \end{matrix}

és mert

A

pont

A_{2}

-nek tükörképe, azért.

\begin{matrix} A A_{2} ⊥ C_{1} B_{1} \end{matrix}

vagy

\begin{matrix} A A_{2} ⊥ C B \end{matrix}

A_{2}, B_{2}, C_{2}

pontok tehát valóban a magasságok talppontjai.
Tételünk értelmében az

A_{2}, B_{2}, C_{2}

pontokban az oldalakra emelt merőlegesek egy pontban találkoznak. De a merőlegesek a háromszög magasságvonalai, tehát a háromszög három magassága egy pontban találkozik.
Hasonló módon lehet a Reuschle-féle tétellel a három magasságnak egy pontban való találkozását bizonyítani.
De másrészt tételünk értelmében még szükséges, hogy a

P, O

és

M

pontok egy egyenesben legyenek, a mi a következő ismeretes eredményt tartalmazza:
A háromszög köré írható kör középpontja, a Feuerbach-féle kör középpontja és a magassági pont egy egyenesben feküsznek.
Végre ugyancsak tételünk következményeképpen:

\begin{matrix} P O = O M \end{matrix}

vagyis:
A Feuerbach-féle kör középpontja a háromszög köré írható kör középpontjától, valamint a magassági ponttól egyenlő távolságban van.
Mind ismeretes eredmények, melyeket külön szoktunk bizonyítani, holott látjuk, hogy azok elég könnyen bizonyítható tételünk egyszerű következményei.
Egymásra merőleges átlókkal bíró négyszögekre vonatkozólag ismeretes a következő tétel.
Ha

P

ilyen négyszög átlóinak metszéspontja, akkor

P

-ből az oldalakra bocsátott

P P_{1}, P P_{2}, P P_{3}

és

P P_{4}

merőlegesek

P_{1}, P_{2}, P_{3}

és

P_{4}

talppontjai, valamint e merőlegeseknek a szemben fekvő oldalakkal való

M_{3}, M_{4}, M_{1}

és

M_{2}

metszéspontjai egy kör kerületében feküsznek.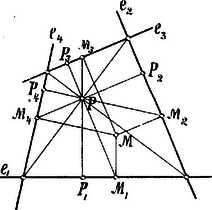

Tételünk alapján még azt is állíthatjuk, hogy az

M_{1}, M_{2}, M_{3}

és

M_{4}

pontokban a megfelelő oldalakra emelt merőlegesek egy pontban ‐

M

-ben ‐ találkoznak.

Budapest.

Weisz Lipót.