Kezdőlap


Cím:	Vázlatok a mathematika történetéből 8. (Dinostratos)
Szerző(k):	Baumgartner Alajos
Füzet:	1898/június, 165 - 167. oldal	PDF \| MathML
Témakör(ök):	Egyéb írások

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Dinostratos.

(Kr. e. IV. század.)

A platoi iskolában a delosi problemán kívül még a többi problémát is tanulmányuk tárgyává tették; ily módon Dinostratos, az iskola egyik tagja, Menaechmos testvére, a Hippias-féle görbét (V. évf. I. lap) tanulmányozva, annak igen érdekes új tulajdonságait fedezte fel, melyek a kör quadraturájára vonatkoznak s így ezek felhasználásával e problémát is egy lépéssel tovább vitte.
A Hippias-féle görbénél a következő arányokat találta (l. 1. ábra) a

D

pontból kiinduló körívekre és az

O

pontból kiinduló megfelelő sugárrészekre vonatkozólag: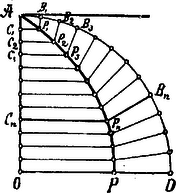

1. ábra

\begin{matrix} D B_{1} : O C_{1} = D B_{2} : O C_{2} = ... = D B_{n} : O C_{n}, \end{matrix}

a hol a

B_{1}

és

C_{1} B_{2}

és

C_{2} ..., B_{n}

és

C_{n}

pontok megfelelően a görbének

P_{1}, P_{2} ..., P_{n}

pontjához tartoznak. Ez arányok természetesen ama

B

és

C

pontokból kiinduló vonalakra is érvényesek, melyek a görbének

A

pontjához tartoznak; ez esetben a

B

és

C

pontok is az

A

ponttal esnek össze, úgy hogy az aránylat ez:

\begin{matrix} D A : O A = D B_{n} : O C_{n} \end{matrix}

és mivel

O A = r

, úgy:

\begin{matrix} D A : r = D B_{n} : O C_{n} . \end{matrix}

Ily módon Dinostratos a

D A

negyedkörívet és a sugarat hozta be az aránylatba; az általános

D B_{n} : O C_{n}

arányba pedig úgy hozott specziális értékeket, hogy a Hippias-féle görbének egy másik főpontját: a

P

pontot választotta. Itt azonban nehézség támad, mert a

P

ponthoz tartozó

D B_{n}

körív is meg az

O C_{n}

sugárrész is nullára fogy le és így e mennyiségek a nevezett arány megállapítására fel nem használhatók.
Hogy azonban mily finom mathematikai érzék fejlődött már ki e korban, azt Dinostratosnak ama ügyes eljárása bizonyítja, mellyel e nehézséget kikerüli. Ez eljárás a megközelítés módszere, mely később hasonló esetekben egész mathematikai disciplinává fejlődött ki. E módszer a jelen esetben abban állt, hogy a görbének általános

P_{n}

pontját nem helyezte rögtön a

P

pontba, hanem csak ahhoz igen közel (1.2. ábra), miáltal a

B_{n}

pont is igen közel jut a

D

ponthoz és a

C_{n}

pont is igen közel az

O

ponthoz, úgy hogy a

P P_{n}

körív mindinkább az

O D

sugárral merőleges és

O C_{n}

-nel egyenlő egyenes vonalnak és a

D B_{n}

körív is az

O D

sugárra merőleges egyenes vonalnak tekinthető és pedig annál inkább, minél közelebb jut a

P_{n}

pont a

P

pont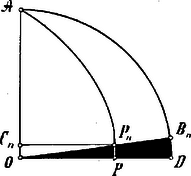hoz.

2. ábra

D B_{n} : O C_{n}

arány ennélfogva a

\begin{matrix} D B_{n} : P P_{n} \end{matrix}

arányhoz közeledik. De az

O D B_{n}

és

O P P_{n}

hasonló derékszögű háromszögekből:

\begin{matrix} D B_{n} : P P_{n} = O D : O P . \end{matrix}

Legyen

O P = ρ

és mivel

O D = r

, úgy

\begin{matrix} D B_{n} : P P_{n} illetőleg D B_{n} : O C_{n} = r : ρ . \end{matrix}

Ez aránylatnak a

\begin{matrix} D A : r = D B_{n} : O C_{n} \end{matrix}

aránylattal való összevetéséből származik végre:

\begin{matrix} D A : r = r : ρ, \end{matrix}

miből:

\begin{matrix} D A = \frac{r^{2}}{ρ} . \end{matrix}

Dinosrtratos tehát az előbbi aránylat alapján egy igen könnyű szerkesztésben és egy igen egyszerű képletben, melyekben csak a kör sugara és a Hippias-féle görbe

ρ

vonala szerepel, megadja a lehetőséget a negyedkör hosszának egyenes vonalban való meghatározására, végeredményben tehát a kör rektifikácziójára. A Hippias-féle görbe tehát a kör rektifikácziójára és ennélfogva az evvel összefüggésben álló (l. V. évf. 3-4. lap: Hippokrates) kör-quadraturára vezetett. Ennek alapján a Hippias-féle görbét Dinostratos óta latin fordításban quadratrix-nak nevezik.
Azonban a probléma éleselméjű megoldása daczára is ismét kritikai szavunkat kell közbevetnünk. Dinostratos a negyedkör hosszának meghatározását oly távolságtól teszi függővé, mely tulajdonképpen meg sem szerkeszthető és ez: az

O P = ρ

távolság. A Hippias-féle görbének bármely

P_{n}

pontját (l. 1. ábra) ugyanis az

O B_{n}

sugár az ennek megfelelő, a

C_{n}

ponton átmenő és az

O D

sugárral párhuzamos vonalak metszéspontjai adják. Minél közelebb jut azonban a

B_{n}

pont a

D

ponthoz és vele együtt a megfelelő

C_{n}

pont az

O

ponthoz, annál hegyesebb és ennélfogva megbízhatatlanabb metszést adnak a nevezett vonalak, ha pedig a

B_{n}

éppen beleesik a

D

pontba és vele együtt a megfelelő

C_{n}

pont az

O

pontba, az

O D

sugár és az

O

-ból kiinduló vonal összeesnek és így a keresett

P

pont meg sem határozható, tehát az

O P = ρ

távolság meg nem szerkeszthető.
Így tehát Dinostratos megoldása is igen érdekes elméleti összefüggéseket tár fel a körre vonatkozó két problémában, de gyakorlatilag elvégezhető szerkesztést ez sem nyújt.
Budapest.

Baumgartner Alajos.