| Cím: | Vázlatok a mathematika történetéből 7. (Menaechmos) | ||
| Szerző(k): | Baumgartner Alajos | ||
| Füzet: | 1898/április, 149 - 151. oldal |  PDF | MathML PDF | MathML |
|
| Témakör(ök): | Egyéb írások | ||
|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. Menaechmos. (Kr. e. IV. század.) A platói iskolának majdnem összes mathematikai vizsgálódásai főképpen a delosi problémával állanak összefüggésben. Majd a probléma új tárgyalása, majd ismét az egyik tárgyalás révén felmerült új anyag és gondolatok gazdagítják a mathematika terén elért eredményeket. Menaechmosnak, a platói iskola egyik tagjának és Eudoxus tanítványának tevékenysége is ily irányban nyilatkozik, a mennyiben egyrészt a kúpot teszi tanulmányai tárgyává, másrészt eme tanulmányok eredményeit felhasználva, a delosi problemának két egészen új megoldását adja. A kúpra alkalmasint Archytas szerkesztésénél lett figyelmessé: valószínűleg annak ott előfrduló metszései érdekelték és ezek ösztönözhették őt, először a delosi problémától függetlenül, ezek tanulmányozására. Csakis az egyenes körkúpot vette tanulmányai alapjául és azon is csakis egy metszést tett, még pedig az alkotó vonalra merőleges sík metszését. Ily módon jutott a kúpszeletekre, melyek egész új tért nyitottak ismét a mathematika élénk fejlődésének. Mivel a kúpon csak egy metszést tett, a háromféle kúpszeletet csak úgy kapta meg, hogy háromféle kúpot metszett ily módon. Hogy egy kúpon is megkapható mind a háromféle kúpszelet, arra Menaechmos nem gondolt. E háromféle kúp származtatása czéljából abból indult ki, hogy a kúp az egyenlőszárú háromszögnek szimmetrikus tengelye körül való forgásából keletkezik; már most, a szerint, a mint ennek az egyenlőszárú háromszögnek csúcsszöge hegyes-, derék- vagy tompaszög, a szerint nevezte el a kúpot is hegyes-, derék- vagy tompaszögűnek és a szerint nyert is mindenkor az alkotóra merőleges sík metszése által ellipsist, parabolát vagy hyperbolát (l. 1. ábra). 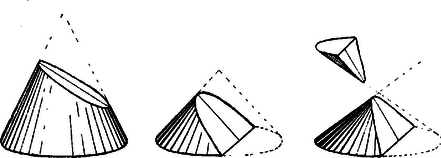 1. ábra Menaechmos tehát az egy metszés daczára is mind a háromféle kúpszeletet ismerte így meg, melyeket a kúp szerint, a melyen származnak, rendre hegyes-, derék- és tompaszögű kúpszeleteknek nevezett el; mind a hármat pedig a "Menaechmos-féle triadok" névvel jelölték meg; a még manapság is használt: ellipsis, parabola, hyperbola elnevezések ugyanis későbbi időkből valók. Hogy Menaechmos mennyit tudott a kúpszeletek tanából, arról összefüggő adataink nincsenek, de hogy ismeretei nem voltak csekélyek, azt abból az eljárásból látjuk, a melyet a kúpszeleteknek a delosi problemára való alkalmazásában követett. Menaechmos is ebből az aránylatból indult ki: 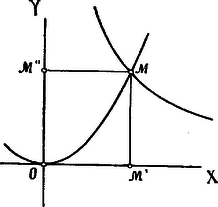 2. ábra Az aránylat első és harmadik arányaiból: Menaechmos még egy második megoldást is adott az által, hogy az aránylat arányait más módon csoportosította. Ugyancsak az aránylatot használta fel első aránylatnak, miáltal az előbb megbeszélt parabolát kapta; második aránylatul azonban az eredeti aránylat második és harmadik arányát vette: 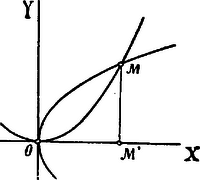 3. ábra A kúpszeleteknek eme alkalmazása arra enged következtetni, hogy Menaechmos a kúpszeletek alaptulajdonságait behatóan ismerte; a delosi probléma tárgyalásának módja által pedig tulajdonképpen az analitikai geometria gondolatát pendítette meg elsőnek. Budapest.
|