Kezdőlap


Cím:	Vázlatok a mathematika történetéből 5. (Archytas)
Szerző(k):	Baumgartner Alajos
Füzet:	1898/január, 81 - 85. oldal	PDF \| MathML
Témakör(ök):	Egyéb írások

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Archytas.

(Kb. 430-365 Kr. e.)

Archytas Tarentben született Kr. e. 430 körül, tehát egykorú volt Platoval, a ki őt Nagygörögországi útjában meglátogatta és a kivel szoros baráti viszonyba lépett. Kiváló jelleme, bölcsessége, önuralma és emberszeretete miatt rendkívüli becsülésben részesült.

Hétszer volt stratéga szülővárosában és három háborúban fővezér. Pythagoras iskolájának tagja volt és mint ilyen tetemes mathematikai ismeretekre tett szert. Horatius szerint az Adriai tengerben az apuliai partoknál egy hajótörés alkalmával vízbe fúlt; valószínűleg Görögországba akart utazni, Platot meglátogatni. Sokféle irattöredékei közül a filozófiai, ethikai és zenei tartalmúakat hamisítottaknak ismerték fel és csak a mathematikaiakat tartják legnagyobbrészt igaziaknak.
Legnevezetesebb munkássága az, melyet a koczka megkétszeresítése körül kifejtett. Plato vetette fel neki is e problemát. Hogy Archytasnak mily bámulatba ejtő tudása volt a mathematikában, azt abból látjuk, hogyan tárgyalta e kérdést. Mindenekelőtt planimetriailag keresi két hosszúságnak:

a

-nak és

b

-nek két középarányosát, úgy hogy egy szög két szárának egyikére (1. ábra) az

O A = a

, másikára az

O B = b

hosszúságot rajzolja; a feladat most ez: a szöget úgy választani, hogy az

A X Y B

tört vonal

A X

és

Y B

része az

O X

szárra és

X Y

része az

O A

szárra legyen merőleges.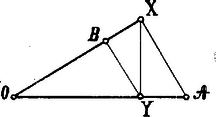

1. ábra

Könnyű belátni, hogy az

O

csúcs szögét tartalmazó háromszögek hasonlóságából eme aránylat származik: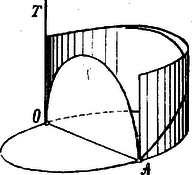

\begin{matrix} O A : O X = O X : O Y = O Y : O B, \end{matrix}

ennélfogva az

O X = x

és

O Y = y

távolságok csakugyan az

a

és

b

két középarányosa. Az

X

pont tehát oly körnek a kerületén fekszik, mely körnek átmérője

O A

; a

B

pont viszont oly körnek a kerületén, mely körnek átmérője

O Y

; ezt azonban nem ismerjük. Archytas a feladatot egy bámulatot keltő, igen komplikált, de nagyon ügyes térbeli szerkesztés segélyével oldotta meg. A szerkesztés leírása a következő: rajzoljunk kört, melynek átmérője

O A = a

; szerkesszünk továbbá ugyancsak az

O A

átmérő fölé (2. ábra) egy félkört, melynek lapja az előbbi kör lapjára merőleges.

2. ábra

E félkört az

O T

függélyes tengely körül forgatjuk, miáltal a félkörvonal a vízszintes körre állított hengerpaláston az avval való metszéspontjai által egy görbe vonalat ír le. Szerkesszünk továbbá a vízszintes síkban egy derékszögű háromszöget (3. ábra), melynek egyik befogója az

O A = a

átmérő, másik befogója az

A

ponthoz tartozó érintőn fekszik, átfogóját pedig úgy kapjuk, hogy e körbe az

O

pontból kiindulólag az

O B = b

távolságot mint húrt rajzoljuk bele és e húrt meghosszabbítjuk

C

-ig a hol az érintőt metszi.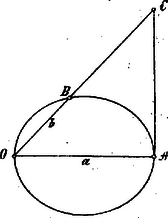

3. ábra

Ha e derékszögű háromszöget

O A

mint tengely körül forgatjuk, az

O C

átfogója kúpfelületet ír le, mely a henger-felületen levő görbét valamely

X

pontban metszi (4. ábra).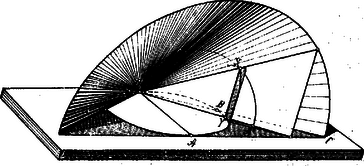

4. ábra

Ez az

X

pont tehát a henger palástján fekszik, ennélfogva vetülete:

Y

pont az

A B O

körvonalba esik; másrészt az

X

pont a görbén, tehát az

O A = O A'

átmérő fölé rajzolt félkörön is fekszik, ennélfogva az

O X

és

X A'

vonalak merőlegesek egymásra. Az

A C

forgása által származott kúpfelületen azonban a

B

pont is egy

B B' D

félkört ír le (5. ábra), melynek síkja az

O B A

síkra merőleges.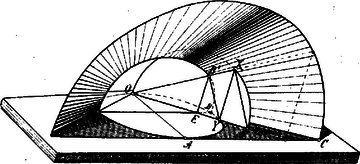

5. ábra

Mivel ugyanerre az

O X A'

sík is merőleges, úgy ezek metszési vonala:

B' E

O B A

síkban fekvő

B D

vonalra is merőleges. Mivel ez a

B' E

B D

átmérőt

B E

és

E D

részekre osztja, úgy:

\begin{matrix} {\bar{B' E}}^{2} = B E \cdot E D . \end{matrix}

Mivel azonban

B D

és

O Y

egy körhöz tartozó és egymást

E

pontban metsző húrok, ezek alapján:

\begin{matrix} B E \cdot E D = O E \cdot E Y; \end{matrix}

ennélfogva

\begin{matrix} {\bar{B' E}}^{2} = O E \cdot E Y, \end{matrix}

tehát az

O B' Y

szög is derékszög, vagyis

B' Y

párhuzamos

X A'

vonallal és mindketten merőlegesek az

O X

szárra.
A különböző háromszögek hasonlóságából a következő összefüggés áll fenn:

\begin{matrix} O A' : O X = O X : O Y \end{matrix}

\begin{matrix} = O Y : O B' \end{matrix}

és mivel

\begin{matrix} O A' = O A = a \end{matrix}

úgy, ha továbbbá

\begin{matrix} O X = x \end{matrix}

tényleg

\begin{matrix} a : x = x : y = y : b \end{matrix}

alapján az

x

és

y

a

és

b

távolságok közötti két középarányos. Ha már most

a

éppen kétszerese a

b

-nek, akkor

y

az a vonal, a melyre épített koczka köbtartalma kétszer nagyobb a

b

-re épített koczkáénál.
Egész csodálatos, majdnem érthetetlen jelenséggel állunk szemben, a mi ezt a szerkesztést illeti. Kísérjük csak figyelemmel végig e szerkesztést: így bepillanthatunk a pythagoreusok gazdag tudományába, melyről a feljegyzések révén, igaz hogy adatokban gazdag, de mégis csak tökéletlen, mert összefüggéstelen képet nyertünk. E szerkesztés alapján azonban arra az eredményre jutunk, hogy a nevezett iskola nemcsak egyes mathematikai igazságokat és tételeket vont be tudományos anyaga körébe, hanem hogy az egyenesen a mathematika tudományos és módszeres iskolája, mondhatni ókori egyeteme volt. Tekintsük csak át a tételeket, melyeket Archytas a leírt szerkesztésnél felhasznál, mint pl.: hogy az átmérőre emelt merőleges félhúr, mértani közép az átmérő két része között, hogy a körhöz tartozó két húr metszékeinek szorzata egyenlő; fontoljuk meg azt az erősen kifejlődött térérzéket és azokat a térbeli összefüggéseket, melyek e szerkesztésnél, kiválóan egy forgási-, továbbá a henger- és kúpfelület átmetszésénél nyilvánulnak és tisztában vagyunk azzal, hogy Archytasban elsőrangú mathematikai tehetséggel ismerkedtünk meg, mely rendszeres és tudományos iskoláztatásban részesült.
Önkéntelenül felmerül az a kérdés, vajjon hogyan végezte Archytas e szerkesztést. Nincsen ugyan adatunk erre vonatkozólag, de azért eléggé megokoltnak látszik az a gondolat, hogy Archytas e szerkesztés végzésére valamiféle mintát használt, mert alig hihető, hogy tisztán rajzzal boldogult volna.
Archytas a számtani, mértani és harmonikus középszámot nemcsak ismerte, hanem helyesen definiálta is. Két szám és azok harmonikus közepével való összefüggését úgy magyarázza, hogy az egyik szám annyiadrészével nagyobb a harmonikus középnél, mint a hányadrészével a másik számnak nagyobb a harmonikus közép e másik számnál; betűkben kifejezve:

\begin{matrix} a = x + \frac{a}{n} \end{matrix}

és

\begin{matrix} x = b + \frac{b}{n}, \end{matrix}

a

a nagyobb,

b

a kisebb szám és

x

ezek harmonikus közepe. E két egyenletből:

\begin{matrix} a - x = \frac{a}{n} \end{matrix}

és

\begin{matrix} x - b = \frac{b}{n} \end{matrix}

származik, ezek osztásából pedig:

\begin{matrix} \frac{a - x}{x - b} = \frac{a}{b}; \end{matrix}

ez utóbbi átalakítva:

\begin{matrix} \frac{a - x}{a} = \frac{x - b}{b}, \end{matrix}

\begin{matrix} 1 - \frac{x}{a} = \frac{x}{b} - 1; \end{matrix}

x

-szel osztva:

\begin{matrix} \frac{1}{x} - \frac{1}{a} = \frac{1}{b} - \frac{1}{x} \end{matrix}

miből csakugyan a harmonikus középnek eme legismeretesebb alakját kapjuk:

\begin{matrix} \frac{1}{x} = \frac{\frac{1}{a} + \frac{1}{b}}{2} . \end{matrix}

Említésre méltó még, hogy Archytas sokat foglalkozott mechanikával, sőt ezt módszeresen kezelte, a mennyiben teljesen geometriai alapokra építette. Elméleti képzettsége mellett azonban praktikus érzéke is volt: gépeket szerkesztett, egész mechanizmusokat; azt mondják, hogy egy automatát és egy fából való repülő galambot is összeállított. Azt is lehet gyanítani, hogy a föld kerületének meghatározását is megkísérelte.

Budapest.

Baumgartner Alajos.