Cím: Vázlatok a mathematika történetéből 4. (Plato)
Szerző(k):  Baumgartner Alajos 
Füzet: 1897/december, 61 - 64. oldal  PDF  |  MathML 
Témakör(ök): Egyéb írások

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Plato.
 

(Folytatás.)
 

Így pl. igen érdekes az ő szereplése a delosi kérdésben (K.M.L.V. évf. 26. lap). Mikor a koczka-alakú oltár megkettőzésének ügyében hozzája fordultak, Plato, előbb említett felfogásához híven ezt mondta: nem is a koczka kétszer akkorává való megnagyobbítását kívánják az istenek, hanem csak azt a gáncsot akarják kifejezni, hogy a görögök keveset foglalkoznak a tudományokkal és nem sokba veszik a geometriát, de mégis megmondja, hogy a feladat megoldására csakugyan egy szám és annak kétszerese között fekvő két középarányosra van szükség, mint a hogyan ezt már Hippokratges is kimutatta (l.K.M.L.V. évf. 27.lap.). Míg azonban Hippokrates nem talált módot e két középarányos meghatározására, addig Plato egy lépéssel tovább halad és a következő eljárást mutatja be: ha az a,x,y,2a hosszúságokat, melyek között ez az összefüggés áll fönn: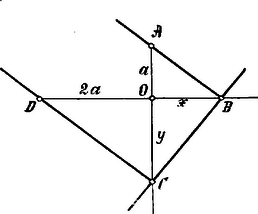
a:x=x:y=y:2a
egy tengelykereszt száraira (1. ábra) az O középpont körül felmérjük, a keletkezett AOB,BOC és COD háromszögek hasonlók, ennélfogva az ABC és BCD szögek derékszögek.
 

Ha tehát sikerül egy BC egyenest úgy választani, hogy a B és C pontjaiban emelt merőlegesek megfelelően az A és D pontokon mennek keresztül, az egyes tengelymetszetek az előbb említett folytonos aránylatnak tesznek eleget és ezzel a delosi probléma szerkesztési úton meg van oldva. Megjegyzendő, hogy e feladat nem végezhető csupán körző és vonalzó segélyével és Plato is csak oly készülék segélyével rajzolta meg, mely összesen négy eltolható vonalzóból állt.
A Pythagoras-féle tétel is érdekelte őt és Pythagoras háromszögeinek (l.K.Math.Lapok. IV. évfolyam 127. lap) számát kibővítette, a mennyiben ő oly egész számú oldalú derékszögű háromszögeket talált, melyekben az átfogó két egységgel nagyobb, mint az egyik befogó; még e háromszögek oldalainak általános képleteit is megadta eme utasítása által: vegyünk egy páros számot, ez legyen az egyik befogó: felezzük meg eme számot, emeljük a felét négyzetre és adjuk e négyzethez az egységet, akkor az átfogó származik; ha azonban a négyzetből az egységet levonjuk, a másik befogót nyerjük; képletei tehát ezek: 2k,k2+1 és k2-1. Érdekes, hogy a 3,4,5 egységnyi oldalú derékszögű háromszög e képletekből is kikerül; ugyanis k helyett 2-t kell venni.
Plato a szabályos testekkel is foglalkozott: ismerte már mind az ötöt és alkalmasint azt is tudta, hogy csak öt lehetséges.
Az egyenlőszárú derékszögű háromszöget is tanulmányozta; ugyanannyit tudott erről mint Pythagoras, de valószínűleg még egy lépésnyire tovább is haladt. Plato ugyanis avval a derékszögű háromszöggel foglalkozott, melynek egy-egy befogója: 5. Azt találta, hogy ennek átfogója (mint tudjuk: 50) igen közel áll 7-hez. Nagyon valószínű, hogy ennek alapján így okoskodott: ha az 5 egységnyi befogójú egyenlőszárú derékszögű háromszög átfogója kb. 7, akkor az 1 egységnyi befogójúé kb. 75 és ebben az esetben a 2=1,4142... irraczionális számnak egy közelítő értékét határozta meg. Úgy látszik, a 50 irraczionális ("kimondhatatatlan") volta nagyon bántotta, mert megjegyzi, hogy rögtön "kimondható" lesz, mihelyt az 50-ből csak 1-et levonunk, de ismét csak "kimondhatatatlan" lesz, ha megint 2-t vonunk le belőle.
Nyilván Platótól való az evvel a dologgal kapcsolatos tétel:
nincs oly négyzetszám, mely egy másik négyzetszámnak éppen a kétszerese, legfeljebb közelítőleg az.
A számok oszthatóságával is foglalkozott és valószínűleg mindazt tudta már, a mire Pythagoras és iskolája jutott és talán éppen a Pythagoras által "baráti" és "tökéletesek"-nek nevezett számok felkeresése alkalmából találta meg azt, hogy az 5040-nek 59 különböző osztója van, melyek között az 1-től 10-ig terjedő egész számok mind megvannak.
Plato ezen kívül még mathematikai definicziókat adott és a mathematika módszereit is megállapította. Definícziói közül említésre méltók ezek: a pont a vonal határa; a vonal a lap határa; a lap a test határa; a test az, a minek három kiterjedése van; a vonal hosszúság szélesség nélkül; a kör az a vonal, melynek részei minden oldal felé a középtől egyenlő távolságra állnak; legérdekesebb az egyenes vonal definícziója, mely szerint az oly vonal, melyben a végpontok a közben eső részt eltakarják.
A mi végre a mathematikai módszereket illeti, Platónak tulajdonítják az ú.n. analitikus (elemző) módszer feltalálását. Ennek lényege az, hogy valamely tétel bebizonyításánál először a keresett dolgot adottnak tekintjük, elemezzük azt és megvizsgáljuk a feltételeket, míg ismert dolgokra jutunk. E módszer menete ilyen: hogy egy D állítást bebizonyítsunk, feltesszük, hogy e D igaz, de akkor igaz egy C állítás, ha C igaz, akkor B is igaz, ha azonban B igaz, akkor A is igaz; de mivel A mint ismert tétel igaz, ennek következtében D is igaz. E módszer ellenkezője a szintetikus (összetevő) módszer, a melyet Plato szintén mint a tudományokban czélhoz vezető módszert megemlít. Ennek útja tehát az, hogy egy A igazságból kiindulunk, ebből B igazságára következtetünk, innen pedig lépésről-lépésre tovább C és D igazságára. Látni való ezekből, hogy az analitikus módszer mindig rávezet az igazságra, mely a szintetikus módszernek kiinduló pontjául szolgál és megjelöli azt az utat, melyen emennek haladnia kell.
Említésre méltó végre még egy módszer, melyet a régiek mind Plato előtt, mind pedig utána néha alkalmaztak; ez az ú. n. apagogikus módszer vagy a deductio ad absurdum, mely abban nyilvánul, hogy a bebizonyítandó tétel ellenkezőjének lehetetlenségét bebizonyítjuk, ennélfogva a bebizonyítandó tétel igaz voltát mondjuk ki.
Plato hatását és jelentőségét a mathematika fejlődésében a következőkben foglalhatjuk össze: e tudomány terjedelme megnövekszik mind újonnan felfedezett tételek és módszerek, mind pedig ama személyiségek által, kiket Plato a mathematikával való foglalkozásba belevon. A mathematika a filozófia egyik fontos segédeszközévé emelkedik és maga is filozófiai alapokat kap definícziók megállapítása és módszerek kijelölése által, végre pedig előkelő helyet foglal el a közoktatásban és ennélfogva a közművelődésben és tudományos életben is. És e hatás nemcsak időleges, hanem befolyással marad a későbbi korokra is ama tekintély révén, melyet Plato megszerzett magának és egész filozófiai rendszerének. Kitartóan kutató és éleselméjű férfiak egész csapata foglalkozik azokkal a problemákkal, melyeket a platói iskolában felvetettek, nevezetesen: a kör négyszögesítésével, a szög három részre való osztásával és a koczka megkétszeresítésével. Az e problemákban elért eredmények közül a nevezetesebbeket ismertetem a következőkben.
 

Budapest.
Baumgartner Alajos.