Kezdőlap


Cím:	Vázlatok a mathematika történetéből 2. (Hippokrates)
Szerző(k):	Baumgartner Alajos
Füzet:	1897/október, 25 - 27. oldal	PDF \| MathML
Témakör(ök):	Egyéb írások

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Több komolysággal, nagyobb óvatossággal és szigorúbb tudással fogott a problemához végre Hippokrates. Ő már ismerte azt a tételt és abból is indult ki, hogy két kör területe úgy aránylik egymáshoz, mint a körök sugarainak vagy átmérőinek négyzetei. Eljárása az volt, hogy valamely $A B$ egyenes fölé félkört rajzolt (ld. ábra), e félkörbe belerajzolta az $A B C$ egyenlőszárú derékszögű háromszöget és ennek befogói fölé, mint átmérők fölé ismét félköröket rajzolt.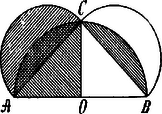

Mivel e körök átmérői között ez az összefüggés áll fenn, hogy

\bar{A B^{2}} = \bar{A C^{2}} + \bar{C B^{2}}

, azért az

A B

fölé rajzolt félkör akkora, mint az

A C

és

B C

fölé rajzolt félkörök együttvéve. Ennélfogva az

A O C

derékszöghöz tartozó negyedkör területe akkora mint az

A C

húr fölé rajzolt félköré. E két terület közös része az

A C

húr és az

A C

körív által bezárt körszelet és ha ezt mind a két területből elvesszük, azt találjuk, hogy az

A O C

egyenlőszárú derékszögű háromszög területe egyenlő a külső félkörből visszamaradt, két körív által határolt félhold alakú idom területével, melyet Hippokrates

μ η ν ι σ κ σ σ

, holdacska (lunula Hippocratis) névvel jelölt meg és mely idom a háromszöggel való egyenlősége miatt négyszögesíthető. Most ezen az úton halad tovább és egy a körbe írt szabályos hatszög oldala fölé rajzol félkört. (1d. ábra).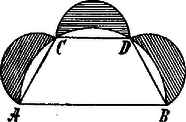

A szabályos hatszög oldala fele az

A B

átmérőnek, ennélfogva a szabályos hatszög oldala fölé rajzolt félkör negyedrésze az

A B

átmérő fölé rajzolt félkörnek és így négy kis félkör együttvéve akkora mint a nagy félkör. Ha a négy kis félkör mindegyikéből levonjuk a szabályos hatszög oldala és a hozzája tartozó körív között fekvő körszeletet, megmarad a négy holdacska területe. Ha viszont a nagy félkörből a három körszeletet vonjuk le, megmarad az

A B C D

trapez vagyis a szabályos hatszög fele, ennélfogva 4 holdacska és a trapez területei között egy ily körszelet a különbség. Hippokrates csakhamar belátta, hogy a szabályos hatszög oldala fölé rajzolt holdacska már nem négyszögesíthető; meg is állapodik e helyen és csak azt jelenti ki: ha e holdacska négyszögesíthető, akkor a kör quadraturáját is megtalálták. Hippokrates még más, nevezetesen oly holdacskákkal is foglalkozott, melyeknek külső köríve nem félkör, hanem kisebb vagy nagyobb annál, de megoldást természetesen nem ért el egyik esetben sem.
Egy másik probléma, mellyel Hippocrates foglalkozott, a koczka megkétszeresítése (duplicatio cubi), az ú. n. delosi probléma. Ennek eredetéhez két monda is fűződik. Az egyik szerint Minos király fiának koczka alakú síremléket építtetett, melyet azonban a király kicsinek talált; kiadta tehát a parancsot, hogy a

100

láb hosszú, ép ily széles és magas koczkát távolítsák el és tegyenek helyébe egy másikat, mely épen kétszer akkora mint a régi. A másik monda szerint a delosi orakulum kijelentette, hogy az atheni pestis megszüntetésére Apollo oltárát, melynek koczka formája van, kétszer akkorára kell megnagyobbítani. Úgy látszik, sokan foglalkoztak a görög mathematikusok közül e feladattal, köztük éppen Hippokrates is, ki azt a megjegyzést tette, hogy a feladatot más alakban is lehet kimondani, t. i. ha két vonal közé, melyek közül a nagyobbik éppen kétszerese a kisebbiknek, két oly középarányost lehetne találni, melyek folytonos arányban állanak az adott vonalakkal, akkor a koczkát is meg lehet kétszeresíteni. Ha ugyanis

a

és

2 a

között e középarányosok

x

és

y

és közöttük e folytonos aránylat fennáll:

\begin{matrix} a : x = x : y = y : 2 a, \end{matrix}

úgy

\begin{matrix} x^{2} = a y \end{matrix}

Ha eme egyenletek elsejét négyzetre emeljük, lesz belőle

x^{4} = a^{2} y^{2}

és ebbe

y^{2}

értéke a második egyenletből behelyettesítve:

x^{4} = 2 a^{3} x

, miből:

x^{3} = 2 a^{3}

; tehát az

a

élű koczkánál kétszer nagyobb koczka éle

x

csakugyan az

a

és

2 a

közé beékelt két középarányos kisebbike. Az út tehát, melyet Hippokrates e probléma megoldására kijelöl, itt is helyes, de a feladat végleges megoldására mégsem vezetett, mert Hippokrates épen azt a két középarányost nem tudta megtalálni: "zavarából - mint Eratosthenes mondja - egy másik, nem csekélyebb zavarba jutott".
Hippokrates igen rendszeresen foglalkozott a mathematikával: könyvet is írt "Stoicheia" czím alatt, a mely a mathematika első elemi könyve volt és a geometria rendszerét is magában foglalta. Idejében nagy híre volt e könyvnek, később azonban Euklides könyve által teljesen háttérbe szoríttatván, feledésbe ment, majd pedig el is veszett végképen. Csak egyes apróbb dolgokat tudunk e könyvről, így pl. hogy Hippokrates a geometriai ábrákat beűkkel jelölte meg: vonalról beszél, "melyen

A B

áll", pontról "melyen

K

áll". Nem egészen bizonyos, hogy Hippokrates volt-e az első, a ki betűket írt az ábrákba; meglehet, hogy már a pythagoreusoktól vette ezt át, a kik a pentagramm csúcspontjaira betűket tettek; igaz, hogy ezek inkább jeligék rövidítései, semmint mathematikai jelölések voltak. Könyvében továbbá szó volt az idomok hasonlóságáról, a kör és részeinek néhány tételéről, nevezetesen ezekről: hogy két kör területei úgy aránylanak egymáshoz, mint a sugaraik négyzetei és hogy hasonló, (azaz: egyenlő középponti szögű) körczikkek úgy, mint a húrjaik négyzetei.
Végre említésre méltó az a tétele is, a mely tulajdonképen a Pythagoras-tétel kibővítése, tehát úgyszólván a Carnot-tétel megpendítése, hogy az általános háromszögben az egyik oldal négyzete nagyobb vagy kisebb a másik két oldal négyzeteinek összegénél, a szerint, a mint ezek tompa- vagy hegyes szöget zárnak be.
Budapest.

Baumgartner Alajos.