Cím: Vázlatok a mathematika történetéből 1. (Hippias)
Szerző(k):  Baumgartner Alajos 
Füzet: 1897/szeptember, 1 - 5. oldal  PDF  |  MathML 
Témakör(ök): Egyéb írások

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

E szofista filozófusról nem tudunk sokat. Elisben született 460 körül Kr. e., Sokrates kortársa volt. Filozófiájának veleje az önmegelégedés volt. Határtalan hiúsága által azonban nevetségessé tette magát; azt állította ugyanis, hogy mindent tud s arra is ajánlkozott, hogy minden kérdésre megfelel. Mit tudott és miként felelt meg esetleg a kérdésekre, azt nem tudjuk, de vannak adataink egy igen érdekes szerkesztésről, melyet Kr. e. 420 körül ő végzett. A gondolatot hozzá alkalmasint Pythagoras iskolája szolgáltatta. Ott ugyanis sokat foglalkoztak szabályos sokszögeknek a körbe való szerkesztésével; láttuk, hogy már a szabályos ötszöggel is foglalkoztak. A feladat az volt tehát: a 360∘-ú szöget szerkesztés útján tetszőleges számú, egyenlő részekre felosztani.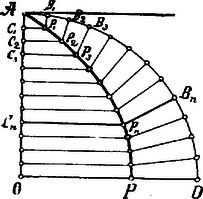
Hippias nyilván e feladatból kiindulva, azt a még általánosabb feladatot tűzte ki magának czélul: bármely szöget szerkesztés segélyével tetszőleges számú, egyenlő vagy pedig bizonyos arány szerint megadott részekre osztani. Ez általános feladat egyik specziális esete a szögnek három egyenlő részre való osztása, a triszekczió; úgy látszik, ez a feladat foglalkoztatta előbb Hippiast és ennek a feladatnak a megoldása -már a mennyiben azt megoldásnak minősíthetjük- foglalta magában egyszersmind az általános feladat megoldását is. A feladat megoldására egy görbe vonalat szerkesztett, mely tulajdonképpen egy mozgási problémára vezethető vissza. Egy körnek OA sugara egyenletes sebességgel forog O körül OD helyzetbe (1. ábra).

 

Ugyanebben az időben a körnek A pontjában vont érintője szintén egyenletes sebességgel halad mindig párhuzamosan maga-magával OD helyzetbe. A két mozgás egyszerre kezdődjék és egyszerre végződjék. A forgó sugár és a mozgó egyenes metszés pontjai adják a Hippias-féle görbét. Egyes pontjait tehát megkapjuk, ha az AD körívet egyenlő részekre (B1,B2,B3,... pontokban) és az OA küllőt is ugyanennyi számú egyenlő részre (C1,C2,C3,... pontokban) felosztjuk, a körív pontjaihoz a sugarakat, a küllő pontjaihoz pedig az érintővel párhuzamos vonalakat meghúzzuk és e megfelelő sugarak és párhuzamosak metszés pontjait (P1,P2,P3,...) megjelöljük. A görbe keletkezéséből tehát azt látjuk, hogy az A ponttól számított körívek mindig arányosak a sugárnak az A ponttól számított megfelelő részeivel:
AB1:AC1=AB2:AC2=AB3:AC3=...=ABn:ACn.

De arányosak a körívek és megfelelő sugárrészek D, illetőleg O ponttól számítva is:
DB1:OC1=DB2:OC2=DB3:OC3=...=DBn:OCn.

A Hippias-féle görbe segélyével tehát körív-nek bizonyos számú és arányú részekre való felosztását egy egyenes vonal-nak ugyanily számú és arányú részekre való felosztására vezethetjük vissza.
A triszekczió feladatát pl. ennélfogva így végezhetjük: az adott és felosztandó CD ívet kiegészítjük derékszöggé és ebbe belerajzoljuk a Hippias-féle görbét, melyen a C pontnak a P1 pont felel meg és ennek ismét a sugáron a B1 pont. Az OB1 vonalat három egyenlő részre osztjuk B2 és B3 pontokban, melyeknek a Hippias-féle görbén a P2 és P3 pontok felelnek meg; ezeknek viszont a köríven a C2 és C3 pontok, melyek már is a körívnek keresett osztási pontjai.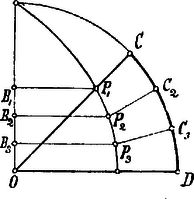
 

Hippias eljárása kétségkívül mathematikailag helyes, de mindazonáltal a felvetett problema szerkesztés által való megoldásának mégsem tekinthetjük. A mathematikai szerkesztéseknél ugyanis kizárólag csak egyenes- és körvonalak használhatók, mert csak ezek oly vonalak, melyeknek minden pontja megrajzolható. Bármely más vonalnak csak tetszésszerinti sok pontja határozható meg, de nem minden pontja. Így pl. a Hippias-féle görbénél sem tudjuk a körívnek minden Bn pontjához az OA küllőn fekvő megfelelő Cn pontját meghatározni, mert nem ismerjük az ABn körívnek arányát az AD negyed körívhez; ennélfogva a görbének sem rajzolhatjuk meg minden Pn pontját. Igaz ugyan, hogy szemünk látóképességének bizonyos határa és a rajzszerek finomságának korlátoltsága miatt abszolut mathematikai pontosságot a rajzban nem érhetünk el s így tulajdonképpen mindig csak relatív pontossággal érjük be és valamely görbe elég sok pontjának meghatározása által mindig elérhetjük e relatív pontosságot; mindazonáltal ily közelítő szerkesztések az előbb említett szerkesztési elvek szempontjából nem tekinthetők szigorú mathematikai szerkesztési megoldásoknak. Hiszen ha pl. a triszekczió-nál elvileg a relatív pontossággal érjük be, akkor a szögnek három egyenlő részre való felosztására a próbálgatás is elég pontos.
 
Hippokrates.
 

Hippokrates életéről keveset tudunk; Chiosból való volt, születésének éve ismeretlen; eleinte kereskedő volt s mint ilyen elvesztette vagyonát, némelyek szerint byzanczi vámszedők csalták meg, mások szerint atheni kalózok rabolták meg 440-ben a samosi háború alkalmával. Ezután Athenben telepedett le s itt Pythagoras iskolájának egyes tagjaival lépett érintkezésbe; ezeknek társaságában sok geometriai dolgot tanult; de mivel tudományát másoknak pénzért tanította, ezek kizárták körükből.
Hippokrates neve a mathematika egyik legérdekesebb problemájával áll összefüggésben: a kör quadraturájával, mely probléma folyton kísértette a mathematikával foglalkozókat. A praktikus érzékű egyiptomiak közelítő módszert kerestek és találtak (l. IV. évf. 6. lap), a theoriára hajlandóbb görögök mathematikailag pontos megoldásra törekedtek. A kör quadraturájának feladata az: oly egyenes vonalú idomot, leginkább téglalapot vagy négyzetet találni, melynek területe szigorúan mathematikailag (nemcsak bizonyos pontosságig) egyenlő egy kör területével. E feladattal együtt jár a kör rektifikácziója: oly egyenes vonalat keresni, mely a kör kerületével egyenlő. Az egyik probléma megoldása a másiké is lenne, mert hiszen a kör területe oly háromszög területével egyenlő, mely háromszögnek alapja a kör kerülete, magassága a kör sugara. A két probléma lényege tulajdonképpen a π geometriai szerkesztése. Csak a legújabb időben sikerült kimutatni, hogy a π oly irracionalis szám, mely semmiféle szerkesztés segélyével meg nem rajzolható. Így tehát nem csoda, hogy a legkiválóbb mathematikusok teljes szellemi erejüket fordították e problémák megoldására a nélkül, hogy teljesen kielégítő eredményt elértek volna.
A problémának megoldás nélkül való maradása miatt azonban semmi okunk sincsen a probléma felvetését hiábavalónak és a vele való foglalkozást haszontalannak tekinteni, mert e kérdés tárgyalása közben az egyes mathematikusok éles elméje, leleményessége annyi gondolatot szült, annyi tételt fedezett fel és annyi tudást halmozott össze, hogy ezek nélkül a mathematika még sokáig nem érte volna el azt a magas színvonalat, melyre ezek révén már akkor emelkedett.
Hippokrates előtt is foglalkoztak már a kör négyszögesítésével. Plutarchos felemlíti, hogy Anaxagoras (Kr. e. 500-428.) 434-ben börtönében a kör quadraturáját rajzolta. Valószínűleg ő is már a probléma szigorú mathematikai megoldására törekedett és nem elégedett meg az egyipotomiakéhoz hasonló közelítő szerkesztéssel.
Antiphon körülbelül ugyanebben az időben foglalkozott a problémával. Egyik állítás szerint a körbe rendre négyzetet, szabályos nyolcz-, tizenhat stb. oldalú sokszöget, másik állítás szerint hat-, tizenkét stb. oldalú sokszöget rajzolt. Így kellene tovább haladni, míg a sokszög oldalai oly kicsinyek, hogy azok a körívekkel esnek össze. Miután pedig bármely szabályos sokszöggel egyenlő területű téglalapot vagy akár négyzetet is lehet szerkeszteni, úgy tehát a kör is négyszögesíthető!
Antiphon evvel az eszmével csak utat jelölt ki, de maga ezen az úton, úgy látszik még annyira sem haladt, hogy a probléma nehézségeivel megismerkedett volna.
Bryson ugyancsak ebben az időben rövidebben végzett a problémával: a körhöz igen sokoldalú körülírt és beírt szabályos sokszöget kell rajzolni és ekkor a körterület e két sokszög területének számtani közepe.
 
Budapest.
 
Baumgartner Alajos.