Kezdőlap


Cím:	Vázlatok a mathematika történetéből 6. (Pythagoras)
Szerző(k):	Baumgartner Alajos
Füzet:	1897/április, 125 - 128. oldal	PDF \| MathML
Témakör(ök):	Egyéb írások

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Pythagorasnak és iskolájának mennyiségtani ismereténél még sokkal érdekesebb geometriai tudománya. Bámulatra méltó az a gondosság és megfigyelési tehetség, melyek segítségével annyi ismeretre tettek szert. Ismerték azt a tételt, hogy a háromszög szögeinek összege $180^{\circ}$ és ezt be is bizonyították, még pedig úgy, hogy a háromszög egyik csúcspontján át a szemközt fekvő oldallal párhuzamos vonalat húztak és a keletkezett váltószögek egyenlőségére utaltak. Manapság is még rendesen ezt a bizonyítást használjuk.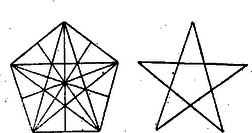
Pythagoras behatóan tanulmányozta a szabályos idomokat és kiválóan azokat, melyeket vagy egyenlőszárú derékszögű- vagy mintaháromszögekre lehet bontani. Ennek alapján az összes idomok alapelemének a derékszögű háromszöget tekintette. Azt találta továbbá, hogy a síkot csak szabályos három-, négy- vagy hatszögek tölthetik ki teljesen. A szabályos ötszöggel is foglalkozott és azt különböző vonalakkal $30$ derékszögű háromszögre bontotta (1. ábra).

A vonalak és idomok e sokaságából, különösen a csillagötszög bontakozik ki, az ú. n. pentagramm, melyet a pythagoreusok ismertető jelül használtak és a tökéletesség és titoktartás szimbólumának tekintettek. E jelet utóbb a középkorban is gonosz szellemek ellen alkalmazták.
A legfontosabb tétel, mely nevéhez is fűződik, mindenesetre az, hogy a derékszögű háromszög átfogójának négyzete egyenlő a befogók négyzeteinek összegével. Már egyedül ez a tétel is hallhatatlanná tette Pythagorast. A tétel fontossága, egyszerű szerkezete, az a körülmény, hogy a derékszögű háromszögre vonatkozó számításoknak majdnem mindegyikének kiindulási pontjául szolgál és végre levezetésének eleganciája elég arra, hogy nevének a mathematikában állandó helyet biztosítson. És hírén mit sem ront, hogy e tétel dolgában nagy szerepe van ismét követőinek a mester iránti kiváló tiszteletének, hogy mindent neki tulajdonítottak és ezáltal a későbbi írókat is befolyásolták, a kik igen gyakran jóval későbben keletkezett dolgokat egyszerűen Pythagorasra vezettek vissza. Ugyanis igen sok okunk van azt hinni, hogy Pythagoras e tételt nem ismerte egészen általánosságban, hanem valószínűleg csak speciális esetek bizonyos rendszerében. Nagyon nehéz ez ügyre teljes világosságot vetni, de talán elég közel állunk az igazsághoz, ha e következő képet alkotjuk magunknak: Pythagoras kétségkívül az egyiptomiaktól tanulta, hogy a

3, 4, 5

egységnyi oldalú háromszög derékszögű háromszög. A számokkal való beható foglalkozása közben a

3, 4,

és

5

számoknak eme összefüggését is mihamar megtalálhatta, hogy

3^{2} + 4^{2} = 5^{2}

. De viszont három szám közötti, ehhez hasonló összefüggést talált a négyzetszámoknak és azok különbségeinek, a páratlan számok sorában:

\begin{matrix} 1 4 9 16 25 36 49 64 81 100 121 144 169 \end{matrix}

\begin{matrix} 3 5 7 9 11 13 15 17 19 21 23 25 \end{matrix}

Ilyen összefüggés pl.

144 + 25 = 169

, vagyis

12^{2} + 5^{2} = 13^{2}

. Visszatérve a geometriára, azt tapasztalhatta, hogy a

12, 5, 13

egységnyi oldalú háromszög is derékszögű háromszög. Vajjon megelégedett-e e tekintetben a rajzzal, mely e háromszöget derékszögűnek mutatta, vagy egyéb meggyőző okai is voltak-e, azt nem tudjuk. Tény azonban az, hogy a négyzetek és a páratlan számok sorának segélyével megoldotta azt a feladatot, hogyan lehet derékszögű háromszögek egész számú oldalait megtalálni. Mivel tudta, hogy két négyzetszám különbsége mindig páratlan szám, csak azokat a páratlan számokat kellett kiválasztania, melyek szintén négyzetszámok. Ezek pl.

9, 25, 49, 81

és a négyzetszámok közül ebben az összefüggésben állanak:

\begin{matrix} 16 + 9 = 25 \end{matrix}

\begin{matrix} 144 + 25 = 169 \end{matrix}

\begin{matrix} 576 + 49 = 625 \end{matrix}

\begin{matrix} 1600 + 81 = 1681 \end{matrix}

vagyis:

\begin{matrix} 4^{2} + 3^{2} = 5^{2} \end{matrix}

\begin{matrix} 12^{2} + 5^{2} = 13^{2} \end{matrix}

\begin{matrix} 24^{2} + 7^{2} = 25^{2} \end{matrix}

\begin{matrix} 40^{2} + 9^{2} = 41^{2} \end{matrix}

És mindegyik esetben meggyőződött arról, hogy ily összefüggések számai mindig derékszögű háromszögek oldalainak számai is.
Pythagoras még általános képletet is adott a derékszögű háromszögek egész számú oldalaira; az egyik befogó mindig páratlan szám, tehát:

2 k + 1

, a másik befogó ekkor:

2 k^{2} + 2 k

, az átfogó pedig:

2 k^{2} + 2 k + 1

. Pythagoras tehát a nevéhez fűzött összefüggést csak azokról az egész számú oldalú derékszögű háromszögekről ismerte, melyekben az átfogó egy egységgel nagyobb mint a nagyobb befogó. Manapság ugyan minden oly derékszögű háromszöget nevezünk pythagorasi háromszögnek, melynek oldalai egész számúak.
Pythagoras azonban az előbb említett háromszögeken kívül még egy más háromszögről is ismerte az oldalok összefüggését: ez az egyenlőszárú derékszögő háromszög. Az összefüggésről a rajz alapján győződött meg: a háromszög minden oldalára megszerkesztette a négyzetet és e négyzeteknek (az ábrában látható) alkalmas felosztása által meglátta, hogy ebben a háromszögben is az átfogó négyzete oly nagy, mint a befogók négyzetei együttvéve.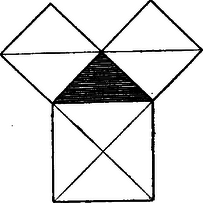

Ha tehát Pythagoras nem is adta a tételt teljes általánosságban, az utókor részéről az semmi esetre sem túlbecsülés, hogy az általános tételt is Pythagoras tételének nevezte.
A Pythagoras-tételre vonatkozó egyéb apróságok is említésre méltók. Eléggé ismeretes az az adat, melyet Plutarchos említ fel, hogy Pythagoras örömében száz ökröt (hekatombát) áldozott fel, a mikor tételét felfedezte. Cicero kifejtette, hogy ez a dolog nem lehetséges, mert ellent mond Pythagoras tanításának és elveinek, mert ő azt a lélekvándorlást tanította, mely szerint a lélek az állatokban is tartózkodik és ennélfogva az állatokat nem szabad megölni. Porphyrios is beleelegyedik a vitába és azt mondja, hogy Pythagoras csak szimbolikusan hozott áldozatot egy tésztából gyúrt ökör képében.
Legérdekesebb Börne-nek az a híres mondása, mely e tárgyhoz fűződik: "Als Pythagoras seinen berühmten Satz entdeckte, opferte er eine Hekatombe; seitdem zittern alle Ochsen, so oft eine neue Wahrheit endeckt wird."
A franczia iskolákban Pythagoras tételét a szamarak hídjának (pont des

\hat{a}

nes) nevezik, "mert a szamarak nem jutnak azon át."
Budapest.

Baumgartner Alajos.