|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. VÁZLATOK A MATHEMATIKA TÖRTÉNETÉBŐL.
Bármely népnek a története a mondából bontakozik ki, melyet a szájhagyomány tartott fönn. Csak aránylag hosszú idő múlva, a mi korunkhoz mérten pedig aránylag rövid idő óta keletkeztek írott emlékek, melyek igazán történeti tényezőkként szolgálhatnak a történészeknek.
Az istenek dicsőítése, vallási czeremóniák, királyok és népek hőstettei, harczi dicsőség, nagy kulturális munkák végzése adtak okot és anyagot a feljegyzésekre, melyek égetett agyagtáblákon, kőbe vésve, papírra vagy fára írva maradtak mi reánk. Idővel bővebb tartalmúak lesznek a feljegyzések: a hitélet, az államkormányzás, a hadászat, de még a közélet, a népszokások tényezői is terjedelmesebb tárgyalásban részesülnek.
A feljegyzések azonban már majdnem teljesen összefüggő történeti adatokat szolgáltatnak, a mikor tudományos tekintetben még mindig nem adnak felvilágosítást. Pedig bizonyos, hogy mihelyt az emberek társadalmi érintkezésbe léptek egymással, közös tevékenységben részt vettek, hogy élelmiszereket, ruházatot, lakást, biztonságot szerezzenek maguknak, akkor már is bizonyos fokú tudásuk volt a természet köréből, hiszen okvetetlenül szükségük volt arra; az élelmiszerek elkészítését, a lakások berendezését, a fegyverek készítését csak sok megfigyelés útján szerzett kémiai és fizikai tapasztalat tette lehetővé. Mindezekkel együtt járt pedig a mennyiség fogalma. A hol bizonyos megszerzett zsákmány szemmeltartásáról van szó, ott okvetlenül szükségesek a számolás, a különböző nagyságok összehasonlítása, a földeknél felmérés, elemibb mértani ismeretek és szerkesztések, majd pedig a jobb időbeosztás czéljából bizonyos időmérés. Így tehát a népek legősibb viszonyai már alkalmasak voltak arra, hogy természetiek mellett, illetőleg ezekkel együtt számtani, mértani és bizonyos csillagászati ismertek származzanak és terjedjenek.
Még inkább terjednek ezek, mikor a népek már egy magas kultúra idejében művészi alkotásokat produkálnak,kiválóan az építészet terén. Most nemcsak az egyszerűbb számtani és mértani elemeket ismerik, hanem a már néha csak igen komplikált okoskodás révén szerzett összefüggéseket is. Egész csodálatos eredményekről tesznek tanúságot a régi népek építkezései és az általuk vagy róluk írt feljegyzések.
Az egyiptomiak. Ez első sorban az egyiptomiakra vonatkozik, a kik már a legrégibb időkben piramisokat, óriási templomokat és palotákat, csatornákat és zsilipeket építettek és kik ennélfogva okvetetlenül sok mathematikai, de még több geometriai tudás birtokában voltak. Ők maguk is, de görög írók is azt mondták, hogy az arithmetikát, a geometriát és a csillagászatot ők találták fel. Herodotos, ki 460 körül Kr. e. Egyiptomban volt, azt írja, hogy Sesostris (II. Ramses) király a Nílus mentén a termékeny földet szétosztotta népe között.
Mivel azonban a folyó minden kiöntése alkalmával a földek hol elmosattak, hol meg nagyobbodtak az iszap lerakódása által, a földek határait mindíg ki kellett igazítani, vagy pedig az értük járó adót arányosan megváltoztatni. Ily módon az egyiptomiaknak sokat kellett geometriával és számítással foglalkozniok és ez is egyik ok, hogy e tudományok náluk annyira kifejlődtek. A görögök a mértant éppen ezért nevezték geometriának: földmérésnek. Az egyiptomiaknál tényleg a praktikus szükségletek, a földfelmérések, építések fejlesztették oly magas fokra a geometriát.
Sokkal érdekesebb adatokat szolgál az Ahmes-féle payrus, mely Ra-a-us vagy másképpen Apapi (görög elnevezésben: Aphobis) a XVI. dinasztiából való Hyksos király idejében, tehát valószínűleg a Kr. e. 2000-1800 években íratott és a mely papyrus jelenleg a londoni "British Museum"-ban van "Papyrus Rhind" czímmel. Ebben a papyrusban, úgy látszik, mindaz össze van gyűjtve, a mit az egyiptomiak számtanból és mértanból tudtak. A bekezdő szavak ezek: "Útmutatás, hogy minden homályos dolgok megismerésére jussunk..... és minden titkokéra, melyek a tárgyakban foglaltatnak". Az egész irat tulajdonképpen egy alkalmazott számtan, mert sok feladatot tűz ki és azok megoldását vagy az arra való útmutatást adja. A mértanra nincs különös tekintettel, nem is tárgyalja külön, hanem egyszerűen számtani feladatokat alkalmaz mértani dolgokra, pl. terület- és köbtartalomszámításokat végez.
Az Ahmes iratából, későbbi papyrusokból, a falakon feljegyzetekből és más népek, kiválóan a görögök irataiból az egyiptomiak mathematikai tudásáról azt a képet alkothatjuk magunknak, melyet a következőkben bemutatni megkísérlek.
A számrendszer dekadikus (tizes) volt, de minden tizes egységre más jel volt. A törtek közül úgy látszik, csak a törzstörtekkel (azokkal, melyeknek számlálója 1) tudtak számolni, csak ezeket tudták leírni és alkalmasint szavuk is csak ezekre volt.
Az illető törzstörtet úgy jelölték, hogy a nevezőt leírták és föléje ilyen jelet:  , vagy még rövidebben egy pontot tettek. A 8-nak pl. ez volt a jele: , vagy még rövidebben egy pontot tettek. A 8-nak pl. ez volt a jele:  , a 10-é pedig ez: , a 10-é pedig ez: 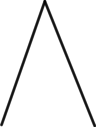 és így az ilyen volt: és így az ilyen volt: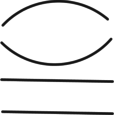 vagy vagy  , az -et pedig így jelölték: , az -et pedig így jelölték: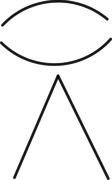 vagy vagy 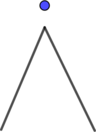 . Két tört volt, melyeknek önálló jelük volt; az egyik az ilyen jellel: . Két tört volt, melyeknek önálló jelük volt; az egyik az ilyen jellel: 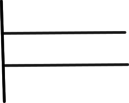 , a másik pedig (ez az egyedüli nem törzstört) ilyen jellel; , a másik pedig (ez az egyedüli nem törzstört) ilyen jellel; 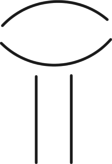 . .
Ha más tört fordult elő, pl. , akkor ezt így fejezték ki:"ossz el 2-t 5-tel", de rögtön kifejezték azt törzstörtek összegéből, így:
Ahmes ad is egy tabellát mindazokkal a törtekkel, melyeknek számlálójuk mindig és nevezőik rendre a páratlan számok -től kezdve -ig és minden tört fel van bontva néha törzstörtre. Néhány példa e táblázatból:
| |
| |
Nem valószínű, hogy Ahmes maga számította ki e táblázatot, sem az, hogy általában egy ember állította össze, hanem valószínűleg az idők hosszú folyamán összegyűjtött adatokból került össze a tabella.
Ha pedig más tört fordult elő, akkor alkalmasint addig bontották azt fel, míg megkapták törzstörtek összegeként, így pl.:
Ahmes iratában találunk számításokat egy ismeretlenű elsőfokú egyenletekkel, a melyeket rendszeresen meg is old. Ezek az úgynevezett hau-számítások; hau ugyanis az ismeretlen neve és szó szerint rakást jelent. Az egyenlet megfogalmazására az iratban foglalt . feladat nyújt példát: "Hau, a hetede, az egésze, kitesz -et". Mai jelentése ez:
A 31. feladat így szól: "Hau, a -a, a fele, a hetede, az egésze, kitesz -at." Azaz:
Úgy látszik tehát, a mindegyik feladatban előforduló "hau" kezdőszó figyelmeztetés arra, hogy mindig erről lesz szó. A megoldás menete a 31. feladatban az, hogy az együtthatókat különválasztja a hau-tól, így: és most az értékét addig szorozza, míg -at kap és ily módon a hau-nak értékét a következő, egy cseppet sem áttekinthető alakban kapja:
| |
A 63. feladat a mai nap társaságszámításoknak nevezett csoporthoz tartozik; ez így szól: "Útmutatás arra: felosztani kenyeret négy személy között, az egyiknek, a másiknak, a harmadiknak, a negyediknek". Az illető részek természetesen nem a -ra vonatkoznak, hanem a hau-ra, úgy hogy a feladat értelme ez:
Találunk feladatot a számtani haladványra is; a 40. feladat így szól: "Kenyér öt személynek; a három elsőtől annyi mint a utolsóé. Mi a különbség?" A feladat így értelmezendő: a hol az -k a számtani sor tagjai.
Végre az igen homályos módon fogalmazott 79. feladat, melyet csak óriási nehézségekkel és csak nagy véletlen folytán lehetett megérteni, ezt tűzi ki : személy közül mindegyiknek van macskája; mindegyik macska egeret eszik; mindegyik egér árpakalászt evett; mindegyik kalászból mérő árpa keletkezhetett volna. Mik ennek a számsornak a tagjai? Ahmes képezi a tagokat, sőt az összegüket is értékkel mint -nek a -szeresét.
Sokkal több és érdekesebb dolgot tudtak az egyiptomiak a geometriából. Szembetűnő itt is mindig a tudásuknak praktikus volta. Idomok leírásával, tételszerű dolgokkal nem foglalkoztak, hanem csak geometriai számításokkal. Reájuk nézve igen fontos volt az idomok területének számítása. Az egyenlőszárú háromszög területe szerintük: , ha a háromszög alapja és a szára. Természetesen hibás volt a képlet, a megasság helyett a nálánál nagyobb szárt vették. A hiba azonban annál kisebb, minél kisebb a háromszög csúcsszöge. Épp ily hibás volt náluk az egyenlőszárú trapez területének számítása, mert ezt: képlet szerint eszközölték, a hol ismét a szárt vették a magasság helyett ( és a trepez két párhuzamos oldala, a szára). A négyzet és téglalap területét azonban helyesen számították.
Foglalkoztak az egyiptomiak e feladattal is: adott körrel egyenlő területű négyzetet szerkeszteni és ezt egyszerűen így oldották meg: a kör átmérőjét megkisebbítették -ével és ez volt már a négyzet oldala. Megközelítőleg elég jó is ez az eljárás, mert a négyzet oldala e szerint. , úgy, hogy a négyzet területe: , a kör területe pedig: lévén, szerintük volt, egészben -nyi eltérés a helyes -től.
Ahmes mindezekre feladatokat hoz, de ad ő stereometriaiakat is: gabonakamráknak a térfogata számítandó ki, csakhogy nem lehet kivenni, hogy milyen ezek alakja és így számításba nem vonhatók.
A legérdekesebb talán valamennyi geometriai számításaik között a "szekt" számítása, mert ebben az első goniometriai kifejezést találjuk fel. A szekt ugyanis egy viszonyszámot jelent egy a gúlák alapjában fekvő vonal fele és egy a gúla felületén fekvő vonal: a piremus között. Úgy látszik, ennek a vonalnak a nevét használták a görögök az egész testnek jelölésésre: piramis. Az összes jelek arra mutatnak, hogy az a bizonyos, az alapban fekvő vonal az alapnégyzet diagonálisa (), a piremus pedig a gúla oldaléla , úgy hogy a
szekt
nem más, mint a gúla oldaléle és az alap által képezett hajlásszög cosinusa. Ha ez a szög meg volt adva, úgy ez által minden egyéb más szög a gúlán már meg van határozva, pl. a gúla oldallapjának hajlása az alaphoz.
Úgy látszik, a szekt nagyon pontosan meg volt határozva, mert az összes egyiptomi gúláknál az oldallapok hajlása az alaphoz minimális eltérésekkel mindig .
Más egyiptomi síremlékeknél is, melyek szintén négyzetalapú, de meredekebb oldallapokkal bíró gúlák, előfordul ily viszony, de az ott valószínűleg az oldallapok hajlásszögének tangense.
Mindeme adatoknak, melyeket eddig elmondtam, forrásul az Ahmes irata szolgál. Későbbi időkből származó papyrusok, falakon található hieroglifek, görög íróknak e tárgyra vonatkozó nyilatkozatai az egész képet az egyiptomiak mathematikai tudásáról csak megerősítik, kiegészítik, elég világossá teszik. Van azonban még egy adat, mely az egyiptomiak geometriájára épen igen érdekes dologban világot vet. Demokritos, az ú. n. "nevető filozófus" az egész akkori tudást felölelő iratainak egyikéban Kr. e. 420 körül avval dicsekszik, hogy "a feltételekből vont következtetések alapján ő olyan vonalszerkesztéseket tud megcsinálni, hogy ebben őt senki sem múlta fölül, még az egyiptomi harpedonapták sem". Érdemes lesz e dolgokról bővebben beszélni.
Az egyiptomiak a piramisaik és templomaik alaplapjainak oldalait pontosan észak-déli és kelet-nyugati irányban állapították meg.
A király éjjel kiment az illető helyre és egyiptomi körülményességgel maga állapította meg a gönczölszekér csillagzatnak bizonyos időban való állása segélyével az észak-déli irányt. Ez meglévén, most a kelet-nyugati irányt kellett meghatározni. Tehát az észak-déli irányra két ponton derékszöget kellett szerkeszteni. E derékszögek szerkesztése a harpedonapták, szószerint: a kötélfeszítők dolga volt. Az egyiptológusok ugyanis sok e tárgyra vonatkozó adatból azt tartják, hogy az egyiptomiak tudták azt, hogy egy és egységnyi oldalakkal bíró háromszög, melyben a derékszöget a és egységnyi hosszú oldalok zárják be és hogy ennek alapján szerkesztették meg a derékszöget. Ha ez így van, akkor valószínűleg egy egységnyi hosszú kötelet vettek, mely és egységnyi részekre volt felosztva, a egységnyi részt az észak-déli irányba helyezték és a másik két résszel zárt háromszöget alkottak, mely ez által megadta a derékszöget. A harpedonapták a feljegyzések szerint már a XII. dinasztia idejében, tehát a Kr. e. XXIV. században szerepeltek. Hogy az egyiptomiak a egységnyi oldalú háromszöget mint derékszögűt ismerték, az nemcsak lehetséges, hanem valószínű is. Mindenestre igen beható tanulmányozásnak eredménye ez az ismeret.
A geometriának az egyiptomiaknál még sok egyéb gyakorlati alkalmazása is volt, így első sorban az ornamentikájukban, melynek négyzetek, rhomboidok, trepezek és körök voltak alkotó elemei (lásd ábra).
Továbbá mechanikus eljárásoknál is alkalmazták a geometriát, hogy úgy mondjuk: a hasonlóság elvét; ha ugyanis valamely nagy alakzatot a falakra akartak rajzolni, akkor a kisebb rajzról való kopírozást úgy végezték, hogy a mintát kicsiny, a falat pedig megfelelően nagyobb négyzetekre osztották fel és e hálózat segélyével rajzolták meg a falon az illető alakzatot.
Végre még említésre méltó, hogy az évet napúnak már az egyiptomiak ismerték fel, sőt arra is eljutottak, hogy az év tartama pontosabban nap, s ezért a Kr. e. 238. év óta minden negyedik évet szökőévnek vettek nappal.
Budapest.
*Lásd a "Kitűzött feladatok" között a . számút. |
 PDF | MathML
PDF | MathML