Kezdőlap


Cím:	Maximum és minimumproblémák elemi tárgyalása 3.
Szerző(k):	Arany Dániel
Füzet:	1894/június, 51. oldal	PDF \| MathML
Témakör(ök):	Szakmai cikkek

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Maximum- és minimumproblémák elemi tárgyalása.

(Vége.)

IV.

Vannak oly maximum- és minimum problémák, melyeknek elemi tárgyalása eszközölhető ugyan, de a követett módszer az eddig ismertettektől teljesen elütő és úgyszólván csak az illető problémára alkalmas. Lássunk két ilyen feladatot, melynek tárgya az optikából van választva.

4. A fénytani hasáb egyik határlapjára eső (belépő) sugárnak a hasáb másik határlapján kilépő sugárral képezett szöge, az eltérítési szög

φ

, akkor legkisebb, ha a belépési szög egyenlő a kilépési szöggel.
Jelelje

i

a szöget, melyet a belépő sugár az első határlapra merőleges egyenessel, a beesési merőlegessel képez,

r

a megtört sugár szögét ugyanazon merőlegessel. Hasonlóképpen jeleljék

r'

és

i'

a hasábban haladó és a második határlapon kilépő sugarak szögeit a második határlapra merőleges egyenessel. Végül legyen

α

a hasáb törőszöge és

φ

az eltérési szög. (1. ábra.)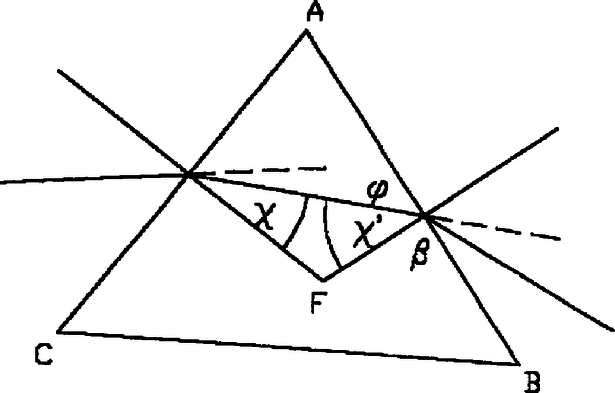

1. ábra

E F D

háromszögből látjuk, hogy

\begin{matrix} r + r' = α \end{matrix}

és a

D E G

háromszögből, hogy

\begin{matrix} φ = i - r + i' - r' \end{matrix}

\begin{matrix} φ = i + i' - α \end{matrix}

A törő hasáb törés mutatója

n

tudvalevőleg

\frac{sin i}{sin r}

vagy

\frac{sin i'}{sin r'}

, mit még a következő egyenletekkel fejezhetünk ki:

\begin{matrix} sin i = n sin r \end{matrix}

\begin{matrix} sin i' = n sin r' \end{matrix}

Ha a 4) egyenletet a 3)-hoz hozzáadjuk és ugyanabból másodszor levonjuk, kapjuk a következőket.

\begin{matrix} sin i + sin i' = n (sin r + sin r'), \end{matrix}

\begin{matrix} sin i - sin i' = n (sin r - sin r') . \end{matrix}

Ez utóbbiak, mint a geometriából ismeretes a következő alakra hozhatók:

\begin{matrix} sin \frac{1}{2} (i + i') cos \frac{1}{2} (i - i') = n sin \frac{1}{2} (r + r') cos \frac{1}{2} (r - r') \end{matrix}

\begin{matrix} cos \frac{1}{2} (i + i') sin \frac{1}{2} (i - i') = n cos \frac{1}{2} (r + r') sin \frac{1}{2} (r - r') \end{matrix}

Ha a most nyert két egyenlet elsejét elosztjuk a másodikkal lesz:

\begin{matrix} tan \frac{1}{2} (i + i') cot \frac{1}{2} (i - i') = tan \frac{1}{2} (r + r') cot \frac{1}{2} (r - r') \end{matrix}

vagy még másképp:

\begin{matrix} tan \frac{1}{2} (i + i') tan \frac{1}{2} (r - r') = tan \frac{1}{2} (r + r') tan \frac{1}{2} (i - i') \end{matrix}

Minthogy levegőből üvegbe lépő sugarakról van szó,

n

a törésmutató nagyobb az egységnél és

i

meg

i'

nagyobbak

r

és

r'

-nél. Tehát

\begin{matrix} \frac{1}{2} (i + i') > \frac{1}{2} (r + r') \end{matrix}

\begin{matrix} tan \frac{1}{2} (i + i') > tan \frac{1}{2} (r + r') \end{matrix}

Ha tehát

i ≷ i'

, a mikor egyszersmind

r ≷ r'

, a 7)-ből következik, hogy

\begin{matrix} tan \frac{1}{2} (r - r') < tan \frac{1}{2} (i - i') \end{matrix}

\begin{matrix} \frac{1}{2} (r - r') < \frac{1}{2} (i - i') \end{matrix}

De ez utóbbi egyenlettel egyidejűleg áll fenn a következő:

\begin{matrix} cos \frac{1}{2} (r - r') > cos \frac{1}{2} (i - i') . \end{matrix}

Ez pedig az 5)-tel egybevetve a következőt eredményezi:

\begin{matrix} sin \frac{1}{2} (i + i') > n sin \frac{1}{2} (r + r') \end{matrix}

\begin{matrix} sin \frac{1}{2} (i + i') > n sin \frac{1}{2} α i ≷ i' \end{matrix}

míg, ha

i = i'

\begin{matrix} sin \frac{1}{2} (i + i') = n sin \frac{1}{2} (r + r') = n sin \frac{1}{2} α \end{matrix}

Így tehát

sin \frac{1}{2} (i + i')

-nek és vele

(i + i')

-nek legkisebb értéke akkor jön létre, ha

i = i'

.
De

φ

(i + i')

-tel egyidejűleg növekedik és fogy és így

φ

-nek minimális értéke akkor áll be, ha

i = i'

5. Az

A

pontból kiinduló fénysugár a törő közegben lévő

B

pontba oly

A C B

úton halad, hogy ez út megfutására szükséges idő a lehető legkisebb.
Jeleljük az

A

pontnak távolságát a törő közeg határától

A D = a

-val, a

B

pontét

B E = b

-vel; a

D E

hosszat

c

-vel. Minthogy a két különféle közegben a fénysugár külömböző

c

és

c'

sebességekkel halad, lesz az

A C B

út megfutására szükségeltetett idő (2. ábra.)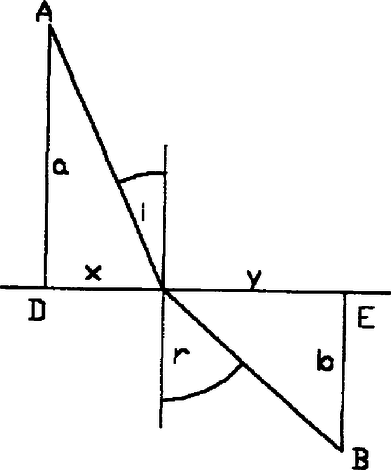

2. ábra

\begin{matrix} t = \frac{A C}{c} + \frac{C B}{c'} \end{matrix}

Minthogy pedig

\begin{matrix} A C^{2} = A D^{2} + D C^{2} = a^{2} + x^{2} \end{matrix}

\begin{matrix} C B^{2} = B E^{2} + C E^{2} = b^{2} + y^{2} \end{matrix}

hol még

\begin{matrix} x + y = c, \end{matrix}

az idő még a következő egyenletek által határoztatik meg

\begin{matrix} t = \frac{\sqrt[]{a^{2} + x^{2}}}{c} + \frac{\sqrt[]{b^{2} + y^{2}}}{c'}, x + y - c = 0 \end{matrix}

Hogy a

t

minimális értéke az

x

és

y

mely értékénél következik be, azt megtudjuk, ha a

t

értékét a következtő alakban írjuk:

\begin{matrix} t = \frac{\sqrt[]{a^{2} + x^{2}}}{c} - k x + \frac{\sqrt[]{b^{2} + y^{2}}}{c'} - k y + k c \end{matrix}

hol

k

tetszésszerinti állandó szám.
A

t

értéke minimum, ha a

\begin{matrix} \frac{\sqrt[]{a^{2} + x^{2}}}{c} - k x \end{matrix}

és

\begin{matrix} \frac{\sqrt[]{b^{2} + y^{2}}}{c'} - k y \end{matrix}

értékek minimumok.
Az

\begin{matrix} {(\frac{\sqrt[]{a^{2} + x^{2}}}{c} - k x)}^{2} - {(k \sqrt[]{a^{2} + x^{2}} - \frac{x}{c})}^{2} = a^{2} (\frac{1}{c^{2}} - k^{2}) \end{matrix}

azonos egyenletből következik, hogy

\begin{matrix} {(\frac{\sqrt[]{a^{2} + x^{2}}}{c} - k x)}^{2} \end{matrix}

és vele együtt a 2) alatti kifejezés akkor minimum, ha

\begin{matrix} k \sqrt[]{a^{2} + x^{2}} - \frac{x}{c} = 0 \end{matrix}

vagyis, ha

\begin{matrix} k = \frac{x}{c \sqrt[]{a^{2} + x^{2}}} \end{matrix}

Hasonlóképpen minimum a 3) alatti kifejezés, ha

\begin{matrix} k = \frac{y}{c' \sqrt[]{b^{2} + y^{2}}} \end{matrix}

\begin{matrix} \frac{x}{\sqrt[]{a^{2} + x^{2}}} = sin i \end{matrix}

és

\begin{matrix} \frac{y}{\sqrt[]{b^{2} + y^{2}}} = sin r \end{matrix}

tehát a 4)-ből és 5)-ből

\begin{matrix} \frac{sin r}{c'} = \frac{sin i}{c} \end{matrix}

\begin{matrix} \frac{sin i}{sin r} = \frac{c}{c'} \end{matrix}

Ez utóbbi egyenlet azonban azon törvénynek kifejezése, mely a beeső és a megtörött sugárnak a beesés merőlegessel képezett szögei között a relácziót megállapítja.
Hogy az

A C B

út befutására szükségeltetett idő rövidebb az

A B

egyenes vagy bármely más

A G B

út befutására szükségeltetett időnél az Huyghens szerint a következőképpen is meg lehet mutatni.
Húzzunk az

F

pontból, melyben az

A B

egyenes a törő közeg határát átmetszi párhuzamosokat a

C A

és

C B

egyenesekkel és emeljük rájuk az

A A'

és

B B'

merőlegeseket. Rajzoljuk meg továbbá az

F F' ⊥ A C

és

C C' ⊥ F B'

egyeneseket. (3. ábra.)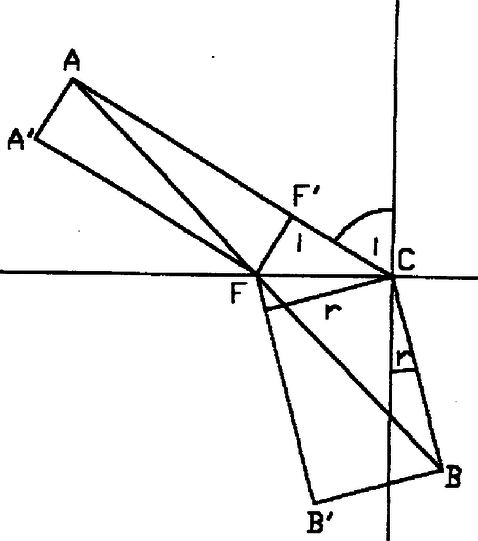

3. ábra

Most közvetlen szemlélet mutatja, hogy az

A F'

és

A' F, C B

és

C' B'

utak befutására szükséges idők:

\begin{matrix} \frac{F' C}{c} és \frac{F C'}{c'} \end{matrix}

továbbá

F' C = F C sin i

\begin{matrix} F C' = F C sin r \end{matrix}

tehát

\begin{matrix} \frac{F' C}{c} = \frac{F C sin i}{c} \end{matrix}

\begin{matrix} \frac{F C'}{c'} = \frac{F C sin r}{c'} \end{matrix}

Ez utóbbiak azonban egyenlők egymással s így az

A C B

út befutására szükségelt idő egyenlő az

A' F B'

út befutására szükségelt idővel. De ez utóbbi kisebb az

A F B

út befutására szükségelt időnél, mert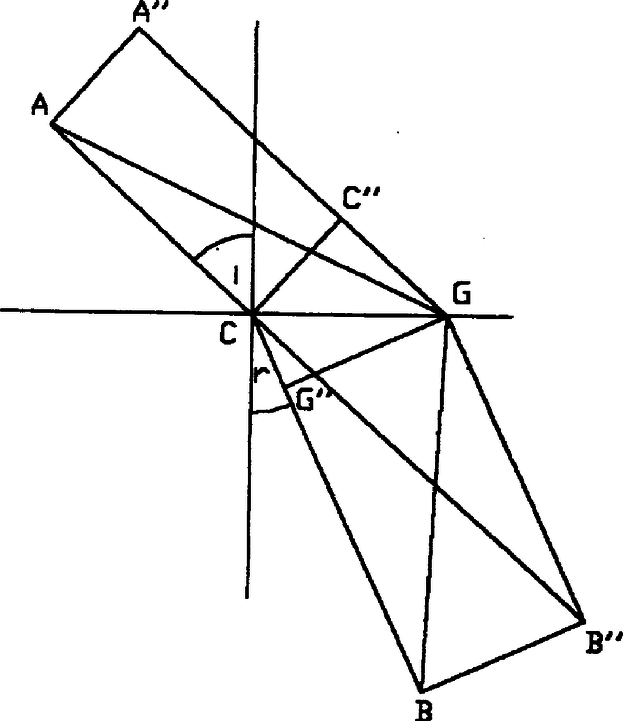

\begin{matrix} A' F < A F \end{matrix}

\begin{matrix} F B' < F B \end{matrix}

4. ábra

Hasonlóképpen látható a 4. ábrából, hogy

A'' C'' G B'

út befutására szükségelt idő egyenlő az

A C B

út befutására szükségelt idővel. Az

A G B

utat a fénysugár tehát hosszabb idő alatt futja be, mint az

A'' G B''

utat, mert

\begin{matrix} A G > A'' G \end{matrix}

és

\begin{matrix} G B > G B'' . \end{matrix}