Feladat: 411. matematika gyakorlat Korcsoport: 14-15 Nehézségi fok: átlagos
Megoldó(k):  Bartha L. ,  Beke G. ,  Biszterszky P. ,  Bódi J. ,  Endrődy T. ,  Fejes L. ,  Füle Károly ,  Grallert F. ,  Hadik Z. ,  Hornyánszky T. ,  Kolonits F. ,  Magos A. ,  Máthé Cs. ,  Mayer G. ,  Müller M. ,  Nagykárolyi Márta ,  Simonfai L. ,  Szász D. ,  Szatmári G. ,  Tamás Gy. (Bp.) 
Füzet: 1957/december, 140 - 142. oldal  PDF  |  MathML 
Témakör(ök): Háromszögek hasonlósága, Pont körüli forgatás, Háromszögek szerkesztése, Gyakorlat
Hivatkozás(ok):Feladatok: 1957/március: 411. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás: Ha a megszerkesztendő háromszög egyik, pl. a PQ oldalát P körül 60∘-kal elforgatjuk, az átmegy a PR oldalba, mivel a háromszög egyenlő oldalú. Ebből következik egy egyszerű szerkesztési eljárás. A P pont körül a Q pont hordozóját: a derékszög egyik szárát elforgatjuk 60∘-kal úgy, hogy messe a másik szárat (a szár elforgatása történhet a szárra bocsátott merőleges segítségével). A metszéspont lesz a háromszög R csúcspontja, a PR oldal ismeretében a háromszög megszerkesztése már könnyen megy.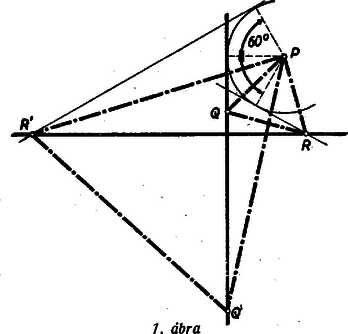
A derékszög három 30∘-os szögtartományra osztható szét. Ha megoldásnak csak a derékszög szárain elhelyezkedő háromszöget engedünk meg, akkor csak az esetben lesz megoldása a feladatnak (mégpedig 1), ha a P pont a derékszög középső 30∘-ának szögtartományában helyezkedik el. Ha megengedjük, hogy a háromszög csúcsa a szárak meghosszabbítására is eshet, akkor mindig van megoldás, mégpedig 2, mert a derékszög szárát P körül két irányban forgathatjuk (1. ábra).

 

 

Ha a P a középső szögtartomány egyik szárára esik, a PQR háromszög egy csúcsa épp a derékszög csúcspontja lesz (2. ábra).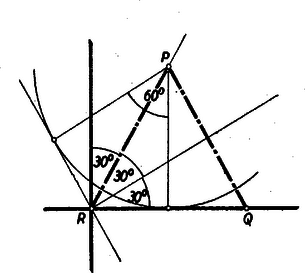
 
 
2. ábra
 

Füle Károly (Bp. V., Apáczai Csere g. II. o. t.)
 

II. megoldás: A P pont ismeretében egyben ismerjük azokat a szögeket is, amilyen szögekben a szabályos háromszög oldalai látszanak a derékszög A csúcsából, ennek ismeretében pedig pl. a PQ oldalnak az AP egyenessel bezárt szögét szerkeszthetjük meg a következőképpen. (3. ábra)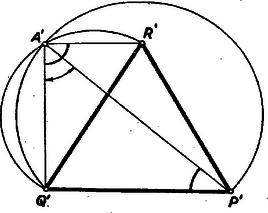
 
 
3. ábra
 

Egy tetszés szerinti P'Q'R' szabályos háromszög Q'R' oldala mint átmérő fölé rajzoljunk az oldal P'-t nem tartalmazó oldalára félkört, a P'Q' oldal fölé pedig rajzoljuk meg azt a körívet, amelyből az oldal akkora szöget zár be, amekkorát PA a derékszög Q-t tartalmazó szárával. A két körív Q-tól különböző A' metszéspontja, ha létezik, felel meg az adott derékszög A csúcsának. Így AP-re rámérve a P csúcsú A'P'Q'∢ nagyságú szöget, ennek szára kimetszi a derékszög szárából a Q pontot, a PQ-ra a Q-ban szerkesztett 60∘-os szög pedig a derékszög másik szárából az R pontot. (4. ábra)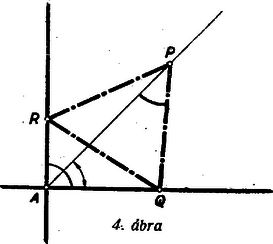
 

 

Szerkesztés szerint az APQ és AQR háromszögek hasonlók a megfelelő vesszős csúcsokkal meghatározott háromszögekhez. Mivel a két háromszög AQ oldala közös, így a PQ és QR oldalak közösek. A köztük levő szög szerkesztés szerint 60∘, így a PQR háromszög szabályos.
A két körív akkor metszi egymást, ha a P'A'Q'∢ 30∘ és 60∘ közé esik. A szélső esetekben Q'-ben érintik egymást, illetőleg a metszéspont R'-be esik. Ha megengedjük azt is, hogy a csúcsok a szögszárak meghosszabbítására essenek, akkor mindkét körívet teljes körré kell kiegészíteni és meg kell rajzolni a P'Q' fölé rajzolt kör tükörképét is. A Q'R' mint átmérő fölé rajzolt körnek ekkor mindkét körrel van Q'-n kívül egy-egy metszéspontja. Így a megoldhatóságra és a megoldások számára kiadódik az az eredmény, amit az előző megoldásban is kaptunk.
 

Megjegyzés: Mindkét szerkesztés hasonlóképpen alkalmazható, ha tetszőleges nagyságú szög száraira illeszkedő háromszöget kell szerkesztenünk.