Kezdőlap


Feladat:	1163. matematika feladat	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Abos Imre , Benczúr András , Dobó Ferenc , Fajszi Cs. , Fejéregyházi Sándor , Gálfi László , Görbe Tamás , Huber Tibor , Makai Endre , Nováky Béla , Raisz Miklós , Reuss P. , Sebestyén Z. , Sebestyén Zoltán , Seprődi L. , Seprődi László , Surányi Andor , Szekeres Veronika , Szentai Judit , Szidarovszky Ágnes , Szidarovszky Ferenc , Varga L. , Vesztergombi György , Vincze I. , Zalán Péter , Zalay M.
Füzet:	1962/november, 128 - 130. oldal		PDF \| MathML
Témakör(ök):	Trigonometriai azonosságok, Kör egyenlete, Szinusztétel alkalmazása, Szögfüggvények, síkgeometriai számítások, Feladat
Hivatkozás(ok):	Feladatok: 1962/március: 1163. matematika feladat

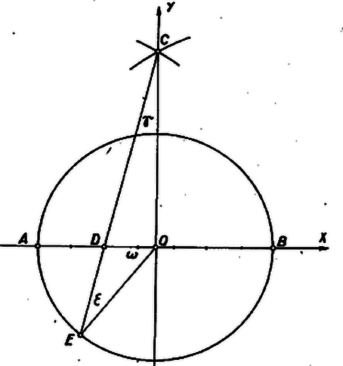
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Ha $n = 4$ , akkor $D$ azonos a kör $O$ középpontjával, ezért $E$ felezi a $C$ -től távolabb fekvő $A B$ ívet, eszerint a közelítő szerkesztés pontos. Ha $n ≧ 5$ , akkor $D$ és $E$ az $O C$ egyenesnek azon a partján van, mint $A$ , ha $n = 3$ , akkor az ellenkező partján. Legyen $A O E ∢ = ω$ , $O C E ∢ = γ$ , $O E C ∢ = ε$ , és válasszuk hosszegységnek az adott kör sugarát. Így $A E = 2 sin ω / 2$ . Az $O C E$ háromszögből $ω = 90^{\circ} - (γ + ε)$ , tehát

\begin{matrix} A E = 2 \sqrt[]{\frac{1 - cos ω}{2}} = \sqrt[]{2 - 2 sin (γ + ε)} = \sqrt[]{2 - 2 sin γ cos ε - 2 cos γ sin ε} . \end{matrix}

(1)

A képlet abban az esetben marad helyes

n = 3

-ra is, ha ez esetben

γ

-t és

ε

-t negatívnak vesszük.

O C D

derékszögű háromszögben

O C = \sqrt[]{3}

O D = O A - A D = 1 - 4 / n = (n - 4) / n

, ezért (mindig a pozitív gyököt véve)

\begin{matrix} tg γ = \frac{n - 4}{n \sqrt[]{3}}, ebből cos γ = \frac{1}{\sqrt[]{1 + {tg}^{2} γ}} = \frac{n \sqrt[]{3}}{\sqrt[]{4 n^{2} - 8 n + 16}}, \\ sin γ = \frac{tgγ}{\sqrt[]{1 + {tg}^{2} γ}} = \frac{n - 4}{2 \sqrt[]{n^{2} - 2 n + 4}} . \end{matrix}

Másrészt az

O C E

háromszögből a szinusz‐tétellel

\begin{matrix} sin ε = \frac{0 C}{0 E} sin γ = \frac{\sqrt[]{3}}{2} \cdot \frac{n - 4}{\sqrt[]{n^{2} - 2 n + 4}}, és így \\ cos ε = \frac{\sqrt[]{4 n^{2} - 8 n + 16 - 3 (n^{2} - 8 n + 16)}}{2 \sqrt[]{n^{2} - 2 n + 4}} = \frac{1}{2} \sqrt[]{\frac{n^{2} + 16 n - 32}{n^{2} - 2 n + 4}} . \end{matrix}

n = 3

esetben képleteink

O D

-t,

sin γ

-t és

sin ε

-t negatívnak, a koszinusz‐értékeket pozitívnak adják, ami éppen megfelel fönti megjegyzésünknek. Ezeket (1)-be beírva, kis átalakítások után

\begin{matrix} A E = \sqrt[]{2 - \frac{(n - 4) (3 n + \sqrt[]{{(n + 8)}^{2} - 96)}}{2 [{(n - 1)}^{2} + 3]}} = & (1) \\ = \sqrt[]{\frac{(n 2 + 4 n + 16 - (n - 4) \sqrt[]{{(n + 8)}^{2} - 96}}{2 [{(n - 1)}^{2} + 3]}} . \end{matrix}

(A belső négyzetgyökjel alatt pozitív szám áll, ha

n ≧ 2

, és a második alakban a kisebbítendő pozitív és négyzete mindig nagyobbnak adódik a kivonandó négyzeténél.)
Jelöljük az adott körbe írt szabályos

n

-szög oldalát

a_{n}

-nel, az erre (2)-ből nyert közelítő értéket pedig

a'_{n}

-vel. Ekkor

a_{n} = 2 sin 180^{\circ} / n

a'_{n} = A E

, és az előírt

n

-ekkel a táblázatba foglalt értékek,

a'_{n} - a_{n}

hibák és

(a'_{n} - a_{n}) / a_{n}

relatív hibák adódnak.

\begin{matrix} \begin{matrix} n & a'_{n} & a_{n} & a'_{n} - a_{n} & \frac{(a'_{n} - a_{n}) 100}{a_{n}} \\ 3 & \sqrt[]{3} & \sqrt[]{3} & 0 & 0 \\ 5 & 1, 1749 & 1, 1756 & - 7 \cdot 10^{- 4} & - 0, 06 % \\ 6 & 1 & 1 & 0 & 0 \\ 7 & 0, 8692 & 0, 8678 & + 14 \cdot 10^{- 4} & + 0, 18 % \\ 8 & 0, 7684 & 0, 7654 & + 30 \cdot 10^{- 4} & + 0, 4 % \\ 9 & 0, 6886 & 0, 6840 & + 46 \cdot 10^{- 4} & + 0, 7 % \\ 10 & 0, 6239 & 0, 6840 & + 59 \cdot 10^{- 4} & + 1, 0 % \\ 36 & 0, 1842 & 0, 1744 & + 98 \cdot 10^{- 4} & + 5, 7 % \end{matrix} \end{matrix}

Ezek szerint az eljárás az egyébként is könnyen szerkeszthető szabályos 3-, 4- és 6-szög oldalát pontosan adja meg, a többi

n ≦ 10

értékekre pedig

1 %

-nál kisebb hibával.

n = 5

-re a közelítő szakasz kisebb, a többiekre nagyobb a valódi oldalszakasznál. (10-nél nagyobb

n

-ekre a hiba valószínűleg egyre gyorsabban nő,

n = 360

-ra már közel

10 %

a többlet.)

Abos Imre (Budapest, Rákóczi F. g. III. o. t.)

II. megoldás. Legyen az adott kör a koordinátarendszerbe az origó köré egységnyi sugárral beírt kör és legyen

A (- 1; 0)

, ekkor

B (1; 0)

, továbbá

C (0, \sqrt[]{3})

. Így

D

abszcisszája

- 1 + 4 / n = (4 - n) / n

, ordinátája 0, a

C D

egyenes egyenlete

\begin{matrix} y - \sqrt[]{3} = \frac{\sqrt[]{3} n}{n - 4} x, amiből x = \frac{(n - 4) (y - \sqrt[]{3})}{\sqrt[]{3} n} . \end{matrix}

Ezt az egységkör

x^{2} + y^{2} - 1 = 0

egyenletébe helyettesítve

E

ordinátájára

\begin{matrix} [{(n - 4)}^{2} - 1 - 3 n^{2}] y^{2} - 2 \sqrt[]{3} {(n - 4)}^{2} y + 3 [{(n - 4)}^{2} - n^{2}] = 0, \end{matrix}

amiből a negatív gyökre van szükségünk, mert így kapjuk a

C

-től távolabbi metszéspontot. A diszkrimináns

1 / 4

része, majd a kívánt gyök:

\begin{matrix} 3 {(n - 4)}^{4} - 3 [{(n - 4)}^{2} + 3 n^{2}] [{(n - 4)}^{2} - n^{2}] = 9 n^{4} - 6 n^{2} {(n - 4)}^{2} = \\ = 3 n^{2} (n^{2} + 16 n - 32), \\ y_{E} = \frac{\sqrt[]{3} {(n - 4)}^{2} - n \sqrt[]{3} \sqrt[]{n^{2} + 16 n - 32}}{4 n^{2} - 8 n + 16} . \end{matrix}

Így

E

abszcisszája, mindjárt összevonással:

\begin{matrix} x_{E} = \frac{n - 4}{n} (\frac{y}{\sqrt[]{3}} - 1) = \frac{n - 4}{n} \cdot \frac{- 3 n^{2} - n \sqrt[]{n^{2} + 16 n - 32}}{4 (n^{2} - 2 n + 4)} = \\ = - \frac{(n - 4) (3 n + \sqrt[]{n^{2} + 16 n - 32)}}{4 (n^{2} - 2 n + 4)}, \end{matrix}

végül az

A E

szakasz hosszának négyzete

\begin{matrix} {(x_{E} + 1)}^{2} + y_{E}^{2} = (x_{E}^{2} + y_{E}^{2} + 1) + 2 x_{E} = 2 + 2 x_{E} = \\ = 2 - \frac{(n - 4) (3 n + \sqrt[]{n^{2} + 16 n - 32)}}{4 (n^{2} - 2 n + 4)}, \end{matrix}

megegyezésben a (2) eredménnyel.

Surányi Sándor (Budapest, Madách I. g. IV. o. t.)